Участник:Soshial

Материал из eSyr's wiki.

Перейти к: навигация, поиск

Содержание

1 Моделирование программ. Размеченные системы переходов. Детерминизм и недетерминизм. Вычисления и трассы. Свойства линейного времени. Выполнимость свойства на трассе.

[править] Моделирование программ. Размеченные системы переходов. Детерминизм и недетерминизм. Вычисления и трассы. Свойства линейного времени. Выполнимость свойства на трассе.

Лекция 2, Слайды 39-50

[править] Размеченная система переходов (LTS)

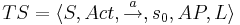
$TS = \langle S, Act, \overset{a}{\rightarrow} ,s_0, AP, L \rangle$

S - множество состояний
Act - множество действий
$τ$ - невидимое действие
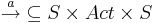$\overset{a}{\rightarrow} \subseteq S \times Act \times S$ - тотальное отношение переходов. Тотальность означает, что из каждого состояния ведёт какое-то действие.
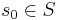$s_0 \in S$ - начальное состояние, либо $I$ - множество начальных состояний
AP - множество атомарных высказываний
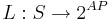$L:S \rightarrow 2^{AP}$ - функция разметки

S, Act - конечные или счётные множества

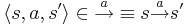
$\langle s, a, s' \rangle \in \overset{a}{\rightarrow} \equiv s \overset{a}{\rightarrow} s'$

Пример LTS: Лекция 2, слайды 40-41

Прямые потомки

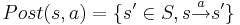$Post(s, a) = \{s' \in S, s \overset{a}{\rightarrow} s'\}$ - такие состояния s', которые непосредственно вытекают из s через переход a
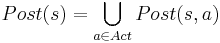$Post(s) = \bigcup_{a \in Act} Post(s, a)$ - все возможные состояния s', которые непосредственно вытекают из s

Система 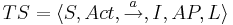$TS = \langle S, Act, \overset{a}{\rightarrow} ,I, AP, L \rangle$ детерминирована:

по действиям тогда и только тогда, когда
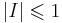
- $|I| \leqslant 1$
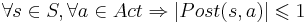- $\forall s \in S, \forall a \in Act \Rightarrow |Post(s, a)| \leqslant 1$ (количество потомков не больше одного)
по атомарным высказываниям
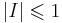
- $|I| \leqslant 1$
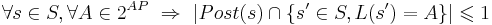- $\forall s \in S, \forall A \in 2^{AP} ~ \Rightarrow ~ |Post(s) \cap \{s' \in S, L(s') = A\}| \leqslant 1$ (количество одинаково размеченных потомков не больше одного)

Недетерминизм - это фича! Полезен для:

моделирования параллельного выполнения в режиме чередования (интерливинга)
- позволяет не указывать скорость выполнения процессов
моделирования прототипа системы
- не ограничивает реализацию заданным порядком выполнения операторов
построения абстракции реальной системы
- модель может быть построена по неполной информации

[править] Вычисления

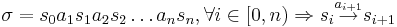
Конечный фрагмент вычисления $σ$ системы переходов TS - это конечная последовательность чередующихся состояний и действий, заканчивающаяся состоянием: $\sigma = s_0 a_1 s_1 a_2 s_2 \dots a_n s_n, \forall i \in [0,n) \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}$
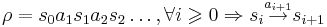
Бесконечный (максимальный) фрагмент вычисления $ρ$ - $\rho = s_0 a_1 s_1 a_2 s_2 \dots, \forall i \geqslant 0 \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}$
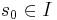
Начальный фрагмент вычисления - фрагмент вычисления, для которого $s_0 \in I$
Вычисление - начальный максимальный фрагмент вычисления (описывает последовательность состояний и действий)

Достижимое состояние (из начального) в системе переходов TS - такое состояние 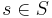$s \in S$ , для которого существует конечный фрагмент вычисления $s_0 a_1 s_1 a_2 s_2 \dots a_n s_n = s$

Reach(TS) - множество всех достижимых состояний в TS

Трасса 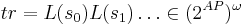$tr = L(s_0) L(s_1) \dots \in (2^{AP})^\omega$

[править] Свойства линейного времени

Свойство 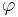$\varphi$ определяет набор допустимых трасс: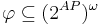 $\varphi \subseteq (2^{AP})^\omega$
Система переходов TS удовлетворяет свойству линейного времени 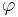$\varphi$ , если: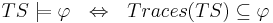 $TS \models \varphi ~~ \Leftrightarrow ~~ Traces(TS) \subseteq \varphi$
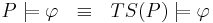по определению программа удовлетворяет свойству φ, если её система переходов удовлетворяет этому свойству: $P \models \varphi ~~ \equiv ~~ TS(P) \models \varphi$ -