Тигры, 01 лекция (от 04 сентября)
Материал из eSyr's wiki.
[править] Раздел 1. Антагонистические игры (АИ)
В АИ принимают участие 2 игрока --- первый и второй игрок. Игр определяется тремя элементами: множество стратегий первого игрока X. Его иногда называют множеством чистых стратегий. Y --- множество стратегий второго игрока. K(x,y), 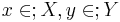 --- платёжная функция. Почти всегда будем предполагать, что X и Y --- компактное множество в конечномерном евклидовом пространстве.
--- платёжная функция. Почти всегда будем предполагать, что X и Y --- компактное множество в конечномерном евклидовом пространстве.
Как происходит игра: первый игрок принимает стратегию x, второй --- y и вычисляет K(x,y). И выигрыш первого игрока --- K(x,y), выигрыш второго --- -K(x, y). В этом и заключается антагонизм, поскольку один хочет максимизировать K, другой --- минимизировать. Как искать стратегию 1 игроку --- если бы он знал, какую стратегию выберет второй игрок, то задача свелась к максимизации функции. Но мы будем рассматривать случай, когда каждый игрок не знает, какую стратегию выберет второй. Получилась неопределенность. И надо понять, что в этом случае делать. В основе принятия решений в этом случае лежит метод, разработанный Г., лежит метод наилучшего гарантированного результата. В этом случае, каждый игрок выбирает стратегию, которая приносит максимальный выигрыш в худшем случае.
Рассмотрим частный случай, который позволяет понять суть метода --- когда X и Y --- конечные множества. Будем считать, что все стратегии занумерованы от 1 до n и от 1 до m соответственно. И платёжную функцию будем обозначать как K(i,j),i = 1..n,j = 1..m. Посмотрим, как работает принцип наилучшего гарантированного результата: предположим, что игрок выбрал стратегию i. Тогда его выигрыш будет в худшем случае minjK(i,j),j = 1..m. В этом случае он должен его максимизировать, то есть maximinjK(i,j) = minjK(i0,j). Эта стратегия существует, максимум есть, таких стратегий может быть несколько, и любая такая стратегия принесёт ему лучший результат. Эту стратегию будем обозначать _I_, нижней ценой игры, нижнее значение игры.
Второй игрок. Предположим, он принял стратегию j. Худший для него вариант --- max_j K(i, j), j=1..m. Выбирать н будет стратегию, которая минимизирует этот максимум --- min_i max_j K(i, j)= max_j K(i, j_0). Эта стратегия существует, минимум есть, Эту стратегию будем обозначать верхней ценой игры ~I~.
Теорема 1. _I_ ≤ ~I~. Математически это доказывается просто. Зафиксируем произвольную пару i, j. min_j K(i, j) ≤ K(i, j) ≤ max_i K(i, j). Отсюда следует, что min_j K(i, j) ≤ max_i K(i, j) при всех i, j. Если это верно при всех i, то можно взять максимум, и он будет верен при любой правой части: max_i min_j K(i, j) ≤ max_i K(i, j). Вспомним также, что это соотношение верно при любых j, тогда можно взят минимум по j, и получаем _I_ ≤ ~I~.
Посмотрим смысловую часть теоремы. Нижняя цена --- тот выигрыш, который гарантирован первому игроку, когда он не знает, как действует второй. Теперь посмотрим на верхнюю цену, это лучшая цена для второго игрока, но можно интерпретировать иначе: пусть первый игрок всегда знает, как действует второй, то есть, он знает j. Тогда он будет искать max_i K(i, j), и тогда в худшем случае он получит min_j max_i K(i, j), то есть, ~I~. То есть, когда игрок знает действия противника, то его выигрыш будет не меньше, чем когда не он знает.
Разность ~I~ - _I_ называется ценой информации. Если верхняя и нижняя цены совпадают, то игроку нет никакой разницы, будут его информацией пользоваться, или нет. А если разность больше нуля, то информация имеет цену.
Рассмотрим примеры. Конечные игры они задаются в виде матрицы. Рассмотрим такой пример:
| 1 | 2 | 0 |
| 2 | 4 | 1 |
Номер строки --- стратегия первого игрока, номер столбца --- стратегия второго. То есть, i=1..2, j=1..3. Как будет действовать первый игрок в условиях неопределённости: Если первый игрок применяет первую стратегию, то он должен рассчитывать на худший выигрыш, на 0, в втором случае получает 1. Тогда по принципу наилучшего гарантированного результата он выбирает вторую стратегию, и нижняя граница --- 1.
Второй игрок. Если применит первую, то проигрыш 2 единицы, если вторую --- 4 единицы, если третью --- 1 единица. В такм случае ~I~ = 1. Здесь _I_ = ~I~
Рассмотрим ещё одни пример:
| 1 | 2 | 3 |
| 2 | 4 | 0 |
_I_ = 1, ~I~ = 2. Здесь уже _I_ < ~I~
Перейдём к случаю, кгда X, Y --- бесконечные множества.
В этом случае первый игрок может раск. на выигрыш inf_y ∈ Y K(x, y). Что должен делать игрок --- максимизировать эту величину, и она в итоге называется нижней ценой _I_. Пусть супремум достигается в x_0, то есть _I_ = inf_y ∈ Y K(x_0, y). Аналогично для второго игрока inf_y ∈ Y sup_x ∈ X K(x, y) = ~I~ = sup_x ∈ X K(x, y_0)
Теорема 2. Аналогична первой, которую мы доказали: _I_ ≤ ~I~ в случае бесконечных антагонистических игр.
Доказательство.
- inf_y ∈ Y K(x, y) ≤ K(x, y) ≤ sup_x ∈ X K(x, y)
- inf_y ∈ Y K(x, y) ≤ sup_x ∈ X K(x, y)
- sup_x ∈ X inf_y ∈ Y K(x, y) ≤ sup_x ∈ X K(x, y)
- _I_ ≤ ~I~
Теорема 3. Если K(x, y) --- непрерывная на X×Y функция, где X, Y --- компакты, то такие функции _w_(x) = min_{y ∈ Y} K(x, y) и ~w~(x) = max_{x ∈ X} K(x, y) --- непрерывны.
Это позволит писать min/max вместо inf/sup.
Докажем первую часть.
Поскольку K(x,y) непр, то ∀ ε > 0: ∃ δ ρ((x_1, y_1), (x_2, y_2)) ≤ δ ⇒ |K(x_1, y_1) - K(x_2, y_2)| ≤ ε
Зафиксируем ε > 0. δ gt; 0 x_!, x_2 ∈ X,: ρ(x_!, x_2) ≤ δ
min_{y ∈ Y} K(x, y) = K(x_1, y(x))
_w_(x_1) - _w_(x_2) = K(x_1, y(x_1)) - K(x_2, y(x_2)) ≤ K(x_1, y(x_2)) - K(x_2, y(x_2)) ≤ ε
Оценим эту разность по-другому:
_w_(x_1) - _w_(x_2) = K(x_1, y(x_1)) - K(x_2, y(x_2)) ≥ K(x_1, y(x_2)) - K(x_1, y(x_2)) ≥ -ε
Из этих двух сотношений получили то, что хотели: |_w_(x_1) - _w_(x_2)| ≤ ε, отсюда следует, что _w_ непрерывна по X.
Следствие. Если _w_, ~w~ непрерывны, то нижняя цена _I_ = max_{x ∈ X} min_{y ∈ Y} K(x, y), аналогично ~I~ = min_{y ∈ Y} max_{x ∈ X} K(x, y)
Перейдём к одному из основополагающих понятий теории АИ --- понятие седловой точки.
Мы рассмотрим АИ на множестве стратегий X×Y.
Пара (x, y) называется седловой точкой игры (функции), если K(x, y_0) ≤ K(x_0, y_0) ≤ K(x_0, y) при всех ∀ x ∈ X, y ∈ Y.
Что означает наличие седловой точки: если первый игрок будет отклоняться от x_0, то его выигрыш может только уменьшиться, а если второй игрок будет отклоняться, то его проигрыш будет только увеличиваться.
Сейчас мы докажем, что это и есть оптимальные стратегии, и цена информации равна 0. А если седловой точки нет, то верхняя цена оказывается строго больше нижней, и цена информации строго неотрицательна.
Рассмотрим случай конечной игры и перепишем условие седловой точки: K(i, j_0) ≤ K(i_0, j_0) ≤ K(i_0, j) при ∀ i = 1..n, j = 1..m.
Рассмотрим следующую платёжную матрицу:
| 1 | -3 | -2 |
| 1 | 5 | 4 |
| 2 | 3 | 2 |
Что такое седловой элемент --- элемент, который максимальный в столбце и минимальный в строке. В данной матрице элемент (i=3, j=1) минимален. Теперь в этой матрице обратим внимание на следующее: вычислим _I_ и ~I~: _I_ = 2, ~I~ = 2. Здесь верхняя цена равна нижней.
Теперь рассмотрим другую матрицу:
2 3 4 1 5 2 2 3 4 1 3 2
Оценим здесь _I_ и ~I~: _I_ = 2, ~I~ = 3. Здесь верхняя цена оказалась больше, чем нижняя.
Обобщим это: если седловая точка существует, то цены совпадают, иначе верхняя больше нижней.
Теорема 4. В матричной антагонистической игре седловая точка существует тогда и только тогда, когда _I_=~I~. Если (i_0, j_0) --- седловая точка, то K(i_0, j_0) = _I_=~I~. И i_0, j_0 --- наилучшие гарантированные стратегии.
Доказательство. Первая часть. a) Предположим, что нижняя цена равна верхней. Пусть i_0 и j_0 --- оптимальные гарантированные стратегии. Тогда из определения имеем следующее: max_i min_j K(i, j) = min_j K(i_0, j). Это нижняя цена игры. В свою чередь, min_j K(i_0, j) ≤ K(i_0, j). В свою очередь, ~I~ = min_j max_i K(i, j) = max_i K(i, j_0) и поскольку мы берём максимум, то Kmax_i K(i, j_0) ≥ K(i, j_0). Но _I_ = ~I~, тогда K(i, j_0) ≤ K(i_0, j) ∀ i = 1..n, j = 1..m. Покажем, что i_0, j_0 --- седловая точка. Откуда это следует? Оно верно при всех i, в частности, при i_0: i=i_0: K(i_0, j_0) ≤ K(i_0, j), оно верно при j=j_0: K(i, j_0) ≤ K(i_0, j_0). Отсюда получаем K(i, j_0) ≤ K(i_0, j_0) ≤ K(i_0, j) ∀ i = 1..n, j = 1..m, то есть (i_0, j_0) --- седловая точка.
Вторая часть первой части теоремы. Необходимое условие. (i_0, j_0) --- седловая точка. Тогда по определению K(i, j_0) ≤ K(i_0, j_0) ≤ K(i_0, j) ∀ i = 1..n, j = 1..m
- max_i K(i, j_0) ≤ K(i_0, j_0) ≤ min_j K(i_0, j)
- min_j max_i K(i, j) ≤ K(i_0, j_0) ≤ max_i min_j K(i, j)
- ~I~ ≤ _I_
Но мы знаем теорему 1, из которой _I_ ≤ ~I~, отсюда _I_=~I~
Первая часть теоремы доказана полностью. Посмотрим, что мы получили. Поскольку _I_=~I~ то там везде имеет место равенство, и, таким образом, мы доказали вторую часть теоремы.
Теорема 5. Если ∃ стратегии i_0, j_0 и константа v такие, что K(i, j_0) ≤ v ≤ K(i_0, j) при ∀ i=1..n, j=1..m, то пара i_0, j_0 образует седловую точку и v = K(i_0, j_0)
Доказательство. Из условия теоремы следует, что K(i, j_0) ≤ K(i_0, j) при ∀ i=1..n, j=1..m, а мы только что доказали, что из этого следует, что (i_0, j_0) --- седловая точка. Т.о. доказали первую часть.
Поскольку можно взять i,j любые, то можно взять i=i_0, j=j_0, и получаем K(i_0, j_0) ≤ v ≤ K(i_0, j_0) ⇒ v = K(i_0, j_0)
На этом с матричными играми пока всё. Возвращаемся к бесконечным играм.
Рассматриваем K(x, y) на X×Y.
Теорема 6. Игра K(x, y) имеет седловую точку тогда и только тогда, когда max_{x ∈ X} inf_{y ∈ Y} K(x, y) = min_{y ∈ Y} sup_{x ∈ X} K(x, y) (то есть точка эта достигается). 2) (x_0, y_0) -- ct ⇒ K(x_0, y_0) = max_x inf_y K(x, y) = min_y sup_x K(x, y)
Доказательство. 1) x_0, y_0. min_x inf_y K(x, y) = inf_y K(x_0, y) ≤ K(x_0, y) ∀ y ∈ Y
- min_y sup_x K(x, y) = sup_x K(x, y_0) ≥ K(x, y_0), ∀ x ∈ X
- Эти две вещи равны, поэтому получаем K(x, y_0) ≤ K(x_0, y) ∀ x ∈ X, y ∈ Y
- x=x_0: K(x_0, y_0) ≤ K(x_0, y)
- y=y_0: K(x, y_0) ≤ K(x_0, y_0)
отсюда СТ.
2) (x_0, y_0) --- СТ
- (аналогично Т4)
Что мы получили, на самом деле. Мы на самом деле получили равенство. Что это означает? Это означает, что ...
- (аналогично Т4)
Это означает, что inf достигается в y=y_0, указанный sup достигается при x=x_0. Это значит, что мы можем записать min_y sup_x K(x, y) = max_x inf_y K(x, y)
Таким образом, теорема доказана полностью.
(Про экзамен)
Первое замечание.
Второе замечание.
| 0 | 1 | 0 |
| 3 | 2 | 3 |
| 0 | 1 | 2 |
Третье.
...
Отсюда следует, что K(x_1, y_2) ≤ K(x_1, y) ⇒ седловая точка.
Несколько примеров.
K(x, y) = 1 - (x-y)^2 X=Y=[0, 1]
_w_(x) = min_{y ∈ [0, 1]} = {1-x^2, x > 0.5 (y=0); 1-(1-x)^2, x≤ 0.5 (y=1)} Теперь он должен взять максимум от этой величины. Посмотрим графически, что здесь получается. То есть, наилучшая стратегия для первого игрока --- x_0 = 1/2. Это в случае, когда игрок не информирован.
Заметим, что здесь же мы описали, как будет действовать второй игрок, когда он информирован.
Как должен действовать, как будет действовать второй, когда он не информирован (как должен действовать первый, когда он информирован).
- 1-x^2=1-(1-x)^2
- 1-x^2=
- I x=1/2
~w~(y) = max_y
Получили, что ~w~ > _w_, значит, седловой точки нет.
Следующие два примера более конкретны. Они имеют в литературе название "дуэльные игры".
Первая дуэль называется "бесшумная дуэль". Два игрока сближаются и могут произвести один выстрел. Произвести выстрелы они могут в момент времени x,y ∈ [0, 1]. Дальше известны функции меткости: p(x), q(y). Что такое p(x) --- вероятность поражения первым игроком второго игрока, если он произвёл выстрел в момент времени x. Функция меткости возрастающая.
Платёж следующий: 1, если 1 игрок поразил второго, -1 если наоборот, 0 в двух остальных случаях. Берётся матожидание. Если x<y, то есть первый игрок стреляет первым. Вспомним, что такое матожидание --- берётся сумма произвольных аргументов на вероятность. То есть, 1*p(x) + (1-p(x))*q(y)*(-1) + 0 * (...) В итоге получается p(x) - (1-p(x))*q(y) (когда x<y). Когда x=y, то получаем p(x)(1-q(x)) - (1-p(x))q(x). Когда x>y, полоучается -q(y)+(1-q(y))p(x).
Эти дуэли бесшумные, поскольку если первый игрок производит выстрел и промахивается, то второй игрок это не слышал. В шумных, если первый выстрелил и промазал, то второй будет стрелять не в момент времени y, а в момент 1, когда вероятность максимальна. В случае, если p(x) = x, q(y) = y, получим
x-y+xy, x<y
K(x, y) = 0, x=y
x-y-xy, x>y
Посчитаем выигрыш. стратегии.
Рассмотрим, как выглядит функция при фиксированном x.
_w_(x) = inf_y K(x, y) = min(-x_2, 2x-1), max_x _w_(x)
x=sqrt(2)-1 --- оптимальное значение для первого игрока, и нижняя цена игрока _I_=2sqrt(2)-3, если то же самое повторить за второго игрока, то получим, что ~I~=3-2sqrt(2) и y=sqrt(2)-1
Вторая модель --- шумная дуэль. Отличается от бесшумной только тем, что если один из игроков производит выстрел и промахивается, то второй игрок об этом узнаёт. Поэтому, когда он узнаёт, то стрелять он будет в момент, когда будет максимально, в момент 1.
Посчитаем вероятности:
p(x) - (1-p(x))q(1), x<y
K(x, y) = p(x)(1-q(x))-(1-p(x))q(x), x=y
-q(y)+(1-q(y))p(1), x>y
p(x) = x, q(y) = y
2x-1, x<y
K(x, y) = 0, x=y
1-2y, x>y
Рассмотрим второго игрока.
- ~w~(y) = sup_x K(x, y) = max(2y-1, 1-2y)
- ~I~ = min ~w~(y)=0, y=1/2
Аналогично для первого игрока _I_=0, x=1/2
Получили седловую точку (1/2, 1/2).
Игра с выбранным моментом времени. Есть два игрока --- подлодка и обороняемый объект. Игра происходит следующим образом: подлодка всплывает, а объект в момент времени y выпускает осветительную ракету освещает акваторию на отрезке y, y+d, если лодка всплывёт в этом интервале, то она будет уничтожена, иначе она уничтожит объект. Если лодка уничтожит объект, то платёж 1, иначе платеж 0
Здесь платёжная функция выглядит следующим образом:
1, x<y или y > y+d K(x, y) = 0, x ∈ [y, y+d]
В любой момент минимум 0, поэтому нижняя цена равна 0, поэтому оптимальным является любой момент. То же для второго игрока --- в любом случае максимум 1, ~I~=1, точка любая, и седловой точки здесь нет.
Переходим к вопросу, связанному с существованием седловых точек. Покажем алгоритм поиска седловых точек. Сейчас более глубоко изучим этот вопрос. Для этого понадобится вспомнить некоторые утверждения из математического анализа, связанные с выпуклостью функций.
Определение 1. Множество Y называется выпуклым, если ∀ y_1, y_2 ∈ Y, α ∈ (0,1): αy1+(1-α)y_2 ∈ Y.
Определение 2.1. Функция f(y), y∈ Y называется выпуклой, если для ∀ y_!, y_2 ∈ Y (y_1 ≠ y_2) , α ∈ (0, 1), f(αy1+(1-α)y_2) ≤ αf(y1)+(1-α)f(y_2)
Определение 2.2. Функция f(y), y∈ Y называется строго выпуклой, если для ∀ y_!, y_2 ∈ Y (y_1 ≠ y_2) , α ∈ (0, 1), f(αy1+(1-α)y_2) < αf(y1)+(1-α)f(y_2)
Определение 2.3. Функция f(y), y∈ Y называется вогнутой, если для ∀ y_!, y_2 ∈ Y (y_1 ≠ y_2) , α ∈ (0, 1), f(αy1+(1-α)y_2) ≥ αf(y1)+(1-α)f(y_2)
Определение 2.4. Функция f(y), y∈ Y называется строго вогнутой, если для ∀ y_!, y_2 ∈ Y (y_1 ≠ y_2) , α ∈ (0, 1), f(αy1+(1-α)y_2) > αf(y1)+(1-α)f(y_2)
Утверждения.
- Сумма двух выпуклых функций есть выпуклая функция
- Сумма выпуклой и строго выпуклой --- строго выпукла.
- Аналогично для вогнутых.
Доказать самостоятельно.
- Строго выпуклая функция на выпуклом множестве имеет ровно одну точку минимума
- Строго вогнутая функция на выпуклом множестве имеет ровно одну точку максимума
Пусть дана f(x), x --- вектор (x_1, ..., x_n), если f ' '(x) --- неотрицательно определённая форма, то f(x) является выпуклой функцией. Если положительно, то строго выпуклой. Если неположительно определённая, то вогнутая, если отрицательно определённая, то строго вогнутая.
Рассмотрим пример. f(x_1, ..., x_n) = x_1^2 + x_2^2 + ... + x_n^2. Пкажем, что это строго выпуклая функция. Найдём f'(x) = (δf/δx_1, ..., δf/δx_n)=(2x_1, ..., 2x_n).
( δ^2f/δx_1δx_1, ..., δ^2f/δx_1δx_n ) (2 ... 0 )
f(x)=( ... ) = ( ... )
( δ^2f/δx_nδx_1, ..., δ^2f/δx_nδx_n ) (0 ... 2 )
Эта форма положительно определённая. Значит, функция строго выпуклая.
Теория игры и исследования операций
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16
Календарь
Сентябрь
| 04 | 11 | 18 | 25 | |
Октябрь
| 02 | 09 | 16 | 23 | 30 |
Ноябрь
| 06 | 13 | 20 | 27 | |
Декабрь
| 04 | 11 | 18 |
Материалы по курсу
Контрольная 1 | Контрольная 2 | Контрольная 3


