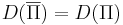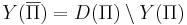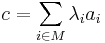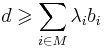Методы Оптимизации, Теормин
Материал из eSyr's wiki.
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15
Календарь
| пт | пт | пт | пт | пт | |
Февраль
| 08 | 15 | 22 | 29 | |
Март
| 06 | 13 | 20 | 27 | |
Апрель
| 04 | 11 | 18 | 25 | |
Май
| 02 | 16 | 23 |
Материалы
Упражнения
||
Задачи | Определения | Утверждения | Теоремы
||
Теормин | Обозначения
[править] Введение в теорию сложности
[править] Индивидуальная и массовая задачи, кодировка задачи, алгоритм решения массовой задачи, временная сложность алгоритма.
Методичка, стр. 4-8
Массовая задача Π:
- список свободных параметров;
- формулировка свойств, которым должно удовлетворять решение задачи.
Π есть множество индивидуальных задач 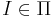 . Индивидуальная задача получается, если всем параметрам присвоить конкретные значения.
. Индивидуальная задача получается, если всем параметрам присвоить конкретные значения.
Пусть Σ — конечный алфавит, а Σ * — множество слов в этом алфавите. Отображение e: 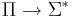 называется кодировкой задачи Π.
называется кодировкой задачи Π.
Алгоритм A решает массовую задачу Π, если для любой индивидуальной задачи 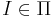 :
:
- A применим к I, то есть останавливается за конечное число шагов
- A дает решение I
Кодировка задачи P — такое отображение 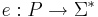 , обладающее следующими свойствами:
, обладающее следующими свойствами:
- Возможность однозначно декодировать, то есть у двух различных ИЗ не может быть одинаковых кодировок.
- e,e − 1 — полиномиально вычислимы
- Кодировка не избыточна, то есть для любой другой кодировки e1, удовлетворяющей 1 и 2 условиям справедливо:
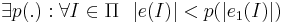
Язык массовой задачи — это множество правильных слов, то есть слов, соответствующих ИЗ, имеющим положительный ответ(подразумевается задача распознавания): 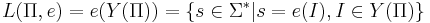
Язык алгоритма — множество слов, принимаемых A, то есть таких, на которых алгоритм останавливается в состоянии qY, что соответсвует "да": 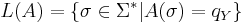
Алгоритм A решает массовую задачу Π, с кодировкой e, если L(e,Π) = L(A) и 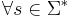 А останавливается
А останавливается
Число шагов алгоритма A для входа 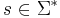 — это tA(s).
— это tA(s).
Временная сложность 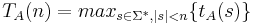 .
.
[править] Задачи распознавания свойств. Классы P и NP.
Методичка, стр. 8-11
Задача распознавания свойств -- массовая задача, предполагающая ответ "да" или "нет", в качестве своего решения.
- D(Π) -- множество всех возможных значений параметров массовой задачи.
- Y(Π) -- множество всех индивидуальных задач, ответом на которые является "да".
Класс полиномиально разрешимых задач (P) -- это такие задачи, временная сложность алгоритма решения которых ограниченна полиномом:
-
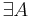 такой, что A решает массовую задачу Π с кодировкой e
такой, что A решает массовую задачу Π с кодировкой e
-
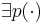 -- полином такой, что
-- полином такой, что 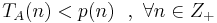
Примеры неполиномиальных задач:
- алгоритмически неразрешимые задачи:
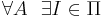 такая, что A не применим к I, например,
такая, что A не применим к I, например, 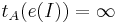
- 10-я проблема Гильберта: по данному многочлену g с целыми коэффициентами выяснить, имеет ли уравнение g = 0 целочисленное решение
- задачи, для которых длина записи выхода превышает любой наперед заданный полином от длины входа
- найти все маршруты в задаче коммивояжёра
- ∀А, решающего П с кодировкой e, ∀p(·) ∃I ∈ П: tA(e(I)) > p( | e(I) | )
Класс недетерминированно полиномиальных задач (NP) -- это такие задачи, для которых существует алгоритм решения на недерменированной машине Тьюринга:
-
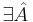 для НДМТ такой, что
для НДМТ такой, что 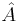 решает массовую задачу Π с кодировкой e
решает массовую задачу Π с кодировкой e
-
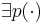 -- полином такой, что
-- полином такой, что 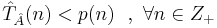
[править] Теорема об экспоненциальной временной оценке для задач из класса NP.
Методичка, стр. 11
Для любой 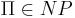 существует ДМТ A, решающая ее с не более чем экспоненциальной временной сложностью:
существует ДМТ A, решающая ее с не более чем экспоненциальной временной сложностью: 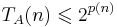 .
.
[править] Класс co-NP. Пример задачи, допускающей хорошую характеризацию. Доказательство утверждения о взаимоотношении классов NPC и co-NP.
Методичка, стр. 12-14
Дополнительная задача 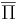 к массовой задаче Π -- задача, получаемая из Π путем введения альтернативного вопроса. То есть если в Π спрашиваем "верно ли x", то в
к массовой задаче Π -- задача, получаемая из Π путем введения альтернативного вопроса. То есть если в Π спрашиваем "верно ли x", то в 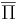 спрашиваем "верно ли, что
спрашиваем "верно ли, что 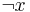 "
"
Класс co-P -- 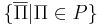
- co-P = P.
Класс co-NP -- 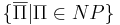 .
.
- co-NP = NP пока не удалось ни доказать, ни опровергнуть, но это вряд ли верно.
-
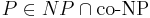
Массовая задача Π допускает хорошую характеризацию, если 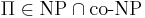
- пример такой задачи -- это задача определения простоты числа.
-
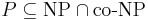
Массовая задача Π' с кодировкой e' полиномиально сводится к задаче Π с кодировкой e, если любая индивидуальная задача 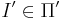 может быть сведена за полиномиальное от её длины время к некоторой задаче
может быть сведена за полиномиальное от её длины время к некоторой задаче 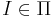 с сохранением ответа.
с сохранением ответа.
Массовая задача Π называется NP-полной (универсальной), если
- принадлежит классу NP:
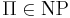
- любая задача из NP полиномиально сводится к Π:
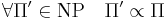
Класс NPC (NP-complete) -- множество всех NP-полных задач.
[править] Критерий NP-полноты. Д-во NP-полноты задачи ЦЛН
Методичка, стр. 15
Критерий NP-полноты. Массовая задача Π NP-полна тогда и только тогда, когда она принадлежит классу NP и к ней полиномиально сводится какая-либо NP-полная задача.
[править] Д-во NP-полноты задачи 3-выполнимость. NP-трудные задачи
Методичка, стр. 17-18
Класс NP-трудных задач содержит:
- задачи распознавания свойств Π, для которых
- не доказано, что
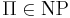
-
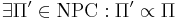
- не доказано, что
- задачи оптимизации, для которых соответствующие задачи распознавания свойств
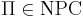
- любые задачи, к которым сводятся по Тьюрингу хотя бы одна NP-полная задача
[править] Взаимоотношение классов P, NP и NPC, NP и co-NP. Класс PSPACE
Легко показать, что 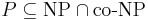 . Рабочая гипотеза, что
. Рабочая гипотеза, что  .
.
Если для некоторой NP-полной задачи Π дополнительная к ней задача 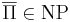 , то NP = co-NP
, то NP = co-NP
Класс PSPACE массовых задач -- класс алгоритмов, требующих не более, чем полиномиальной памяти.
Гипотеза. 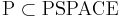 (то есть, не факт, что вложение строгое, но скорее всего так). При этом NP-полные, NP-трудные, NP-эквивалентные задачи
(то есть, не факт, что вложение строгое, но скорее всего так). При этом NP-полные, NP-трудные, NP-эквивалентные задачи 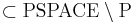
[править] Псевдополиномиальные алгоритмы. Пример для задачи о рюкзаке
Псевдополиномиальный алгоритм - полиномиальный алгоритм, проявляющий экспоненциальный характер только при очень больших значениях числовых параметров.
Пусть M(I) -- некоторая функция, задающая значение числового параметра индивидуальной задачи I. Если таких параметров несколько, в качестве M(I) можно взять или максимальное, или среднее значение, а если задача вовсе не имеет числовых параметров (например, раскраска графа, шахматы и т.п.), то M(I) = 0. Алгоритм называется псевдополиномиальным, если он имеет оценку трудоемкости Tmax(I) = O(p( | I | ,M(I))), где 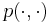 -- некоторый полином от двух переменных.
-- некоторый полином от двух переменных.
[править] Сильная NP-полнота. Теорема о связи сильной NP-полноты задачи с существованием псевдополиномиального алгоритма ее решения
Полиномиальное сужение массовой задачи Π -- множество таких индивидуальных задач I, числовые параметры которых не превосходят полинома от длины входа: 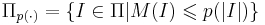
Массовая задача Π называется сильно NP-полной, если её полиномиальное сужение является NP-полным. Примеры:
- задача выполнимости, задача 3-выполнимости -- совпадают со своими полиномиальными сужениями
- задача булевых линейных неравенств -- ВЫП сводится к её полиномиальноу сужению, где числовые параметры (правая часть неравенств) линейны.
- задача о целочисленном решении системы линейных уравнений -- , т.к. БЛН сводится к ней
- задача коммивояжёра (TSL) -- совпадает со своим сужением
Задача о рюкзаке -- слабо-NPC.
Теорема. Если NP не совпадает с P, то ни для какой сильно-NPC задачи не существует псевдополиномиального решения.
[править] Определение ε-приближенного алгоритма и полностью полиномиальной приближенной схемы (ПППС). Связь между существованием ПППС и псевдополиномиальностью
Методичка, стр. 22-24
Задача дискретной оптимизации -- решение каждой индивидуальной задачи 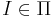 является произвольная реализация оптимума
является произвольная реализация оптимума 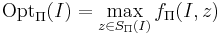 , где
, где
- SΠ(I) -- область допустимых значений дискретной переменной z
- fΠ -- целевая функция задачи оптимизации
- max вообще говоря вполне может быть заменён на min
Алгоритм A называется приближённым алгоритмом решения массовой задачи Π, если для любой задачи 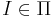 он находит точку
он находит точку 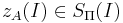 , лежащую в области допустимых значений, принимаемую за приближённое решение.
, лежащую в области допустимых значений, принимаемую за приближённое решение.
Утверждение. Если 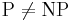 , то ни для какой константы C > 0 не существует полиномиального приближённого алгоритма решения задачи о рюкзаке с оценкой
, то ни для какой константы C > 0 не существует полиномиального приближённого алгоритма решения задачи о рюкзаке с оценкой 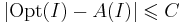 .
.
Приближённый алгоритм A решения массовой задачи Π называется 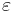 -приближённым алгоритмом решения задачи, если
-приближённым алгоритмом решения задачи, если 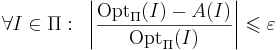 .
.
[править] Теорема об отсутствии ПППС для задач оптимизации, соответствующих сильно NP-полным задачам распознавания
Методичка, стр. 24
Теорема Если для Π оптимизации
- соответствующая ей задача распознавания свойств является сильно NP-полной
- существует полином
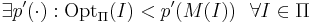
то при условии, что 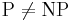 для Π не существует ПППС
для Π не существует ПППС
[править] Основы линейного программирования
[править] Определение озЛП. Принцип граничных решений. Алгебраическая и битовая сложность ЛП. Результаты о сложности для задач, близких к ЛП
ЛП (линейное программирование) -- теория, приложения и методы решения системы линейных неравенств с конечным числом неизвестных : 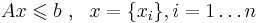 , существует ли
, существует ли 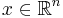 , удовлетворяющий данной системе линейных неравентсв
, удовлетворяющий данной системе линейных неравентсв
озЛП (основная задача линейного программирования) : найти такой вектор 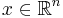 -- решение задачи линейного программирования
-- решение задачи линейного программирования 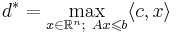 , максимизирующее линейную функцию
, максимизирующее линейную функцию 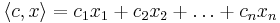
Утверждение (принцип граничных решений). Если озЛП имеет решение, то найдется такая подматрица AI матрицы A, что любое решение системы уравнений AIx = bI реализует максимум 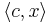 .
.
Алгебраическая сложность -- количество арифметических операций.
Битовая сложность -- количество операций с битами. Битовая сложность задач ЛП, ЛН полиномиальна.
Вопрос о существовании алгебраически-полиномиального алгоритма для ЛП остается открытым.
[править] Геометрическое описание симплекс-метода
(Копипаста из [ru.wiki], там-же есть хорошая иллюстрация.)
Симплекс-метод -- метод решения озЛП.
Каждое из линейных неравенств в 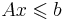 ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным конусом.
Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его ребрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.
ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным конусом.
Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от c порождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его ребрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.
[править] Теорема о границах решений задач ЛП с целыми коэффициентами
Методичка, стр. 28-29
Δ(D) = max | det(D1) | , где D1 — квадратная подматрица D.
Теорема (о границах решений). Если задача озЛП 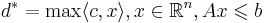 размерности (n, m) с целыми коэффициентами разрешима, то у нее существует рациональное решение x * в шаре:
размерности (n, m) с целыми коэффициентами разрешима, то у нее существует рациональное решение x * в шаре: ![\| x^{*}\| \leqslant \sqrt{n} \Delta([A|b])](/w/images/math/e/0/c/e0cfc825906139f9a1ad88f1ff4bac17.png) и
и 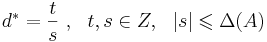
[править] Теорема о мере несовместности систем линейных неравенств с целыми коэффициентами
Методичка, стр. 29
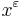 --
-- 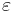 -приближенное решение системы ЛН, если
-приближенное решение системы ЛН, если
- в строчной записи:
![\langle a_i , x^{\varepsilon} \rangle \leqslant b_i + \varepsilon~,~~ \forall i \in [1,m]](/w/images/math/4/a/c/4ac9484c50325adc33b8a9fd58ccfa44.png)
- в матричной записи:
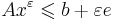 , где e -- вектор-столбец из единиц
, где e -- вектор-столбец из единиц
Теорема. Если система линейных неравенств имеет 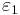 приближенное решение (
приближенное решение (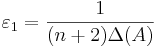 ), то эта система разрешима, то есть имеет точное решение.
), то эта система разрешима, то есть имеет точное решение.
[править] Описание метода эллипсоидов
- Методичка, стр. (30-32) 32-33
- вики:Метод эллипсоидов
Решает задачу линейного программирования за полиномиальное число шагов.
Суть алгоритма в том, чтобы окружить данный многогранник эллипсоидом, а затем постепенно сжимать этот эллипсоид; оказывается, на каждом этапе объем эллипсоида уменьшается в константное число раз.
Лемма1. Если система 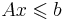 совместна, то в шаре
совместна, то в шаре ![E_0 = \| x \| \leqslant \sqrt{n} \Delta([A|b])](/w/images/math/2/5/d/25d44ce397fc0a3af29658c9267b9d23.png) найдется ее решение.
найдется ее решение.
Таким образом получаем, что если система совместна, то эта лемма позволяет локализовать хотбы бы 1 из ее решений
Введем функцию невязки в точке x -- t(x) = maxi((Ax)i − bi). Точка 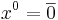 -- это центр шара E0. Если
-- это центр шара E0. Если 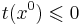 , то x0 -- решение. Если это не так, то возьмем s:
, то x0 -- решение. Если это не так, то возьмем s: 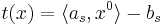 , значит x0 не удовлетворяет s-ому неравенству системы. Всякий вектор x, удовлетворяющий неравенству s, должен лежать в полупространстве
, значит x0 не удовлетворяет s-ому неравенству системы. Всякий вектор x, удовлетворяющий неравенству s, должен лежать в полупространстве 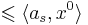 . Пересечение этого полупространства с нашей сферой дают полуэлипсоид. Вокруг получившегося полуэлипсоида описываем новую сферу и повторяем алгоритм заново.
. Пересечение этого полупространства с нашей сферой дают полуэлипсоид. Вокруг получившегося полуэлипсоида описываем новую сферу и повторяем алгоритм заново.
[править] Теория двойственности ЛП
- Методичка, стр. 35-36
- http://www.mathelp.spb.ru/book1/lprog5.htm
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу (линейного программирования), называемую двойственной или сопряженной по отношению к исходной или прямой задаче.
Двойственной задачей к задаче линейного программирования 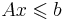 на максимум
на максимум 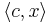 (в форме ОЗЛП можно записать:
(в форме ОЗЛП можно записать: 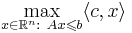 ) называется задача линейного программирования на минимум:
) называется задача линейного программирования на минимум: 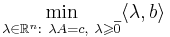
Утверждение Двойственная задача к двойственной задаче совпадает с прямой задачей линейного программирования.
Теорема (двойственности ЛП). Задача ЛП разрешима тогда и только тогда, когда разрешима двойственная к ней. При этом в случае разрешимости оптимальные значения целевых функций совпадают: 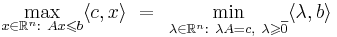
[править] Сведение озЛП к однородной системе уравнений с огрничением x>0
Методичка, стр 36-37
Утверждение. Задача ЛП оптимизации эквивалентна решению системы линейных неравенств.
Утверждение. Задача ЛП оптимизации эквивалентна решению системы линейных уравнений в неотрицательных переменных.
Утверждение. Задача ЛП эквивалентна поиску неотрицательного ненулевого решения однородной системы линейных уравнений.
[править] Идея метода Кармаркара
- Методичка, стр 37-38
- http://logic.pdmi.ras.ru/~yura/modern/02seminar.pdf
Метод Кармаркара.
- На основании предыдущего утверждения (см. вопрос о сведении озЛП к однородной системе), есть возможность свести задачу ЛП
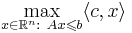 к поиску решения СЛАУ
к поиску решения СЛАУ 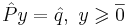 , которая, в свою очередь, сводится к однородной СЛАУ:
, которая, в свою очередь, сводится к однородной СЛАУ: 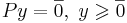
- Введем функцию Кармаркара:
![k(x) = \frac{\left[ (\langle p_1, x \rangle)^2 + \dots + (\langle p_K, x \rangle)^2\right]^{N/2}}{x_1 \cdot x_2 \cdot \dots \cdot x_N}](/w/images/math/d/2/a/d2a0123f059db49edd12e3c433da99a0.png) , где
, где
- N -- число столбцов в P
- K -- число строк в P
-
![p_i, ~ i \in [1,K]](/w/images/math/7/c/3/7c34a57cf32e76b597d04a54ca04b9c2.png) -- строки матрицы P
-- строки матрицы P
- применяя теорему о мере несовместимости и алгоритм округления можно показать, что для решения достаточно найти такой
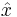 , для которого
, для которого 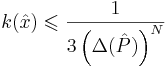
- при этом можно так же показать полиномиальный алгоритм поиска данного приближения, который в курсе не рассматривается.
[править] Следствия систем линейных неравенств. Афинная лемма Фаркаша (без доказательства)
- Методичка, стр. 34-35
- http://imcs.dvgu.ru/lib/nurmi/finmath/node41.html
Система линейных неравенств 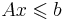 называется разрешимой, если
называется разрешимой, если 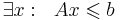
Линейное неравенство 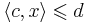 является следствием разрешимой системы ЛН
является следствием разрешимой системы ЛН 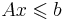 , если для всех x, для которых выполняется сама система, выполняется и следствие:
, если для всех x, для которых выполняется сама система, выполняется и следствие: 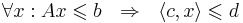
Афинная лемма Фаракша.
Линейное неравентсво 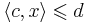 является следствием разрешимой в вещественный переменных ЛН
является следствием разрешимой в вещественный переменных ЛН 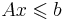 , тогда и только тогда, когда существуют
, тогда и только тогда, когда существуют 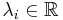 :
:
[править] Лемма Фаркаша о неразрешимости
Методичка, стр. 35
Лемма.
Система линейных неравенств 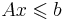 неразрешима тогда и только тогда, когда разрешима система:
неразрешима тогда и только тогда, когда разрешима система:
-
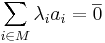 (нулевой вектор)
(нулевой вектор)
-
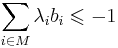
-
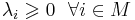
[править] Элементы математического программирования
[править] Классификация задач математического программирования. Преимущества выпуклого случая
Методичка. стр 39-41
Задача математического программирования (ЗМП) -- по заданной f(x) найти 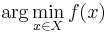 , то есть:
, то есть:
- найти
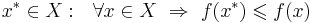 -- решение
-- решение
- f * = f(x * ) -- (оптимальное) значение целевой функции f(x)
- где X -- допустимое множество (множество ограничений)
Классификация проводится по типу допустимого множества X:
- дискретные (комбинаторные) -- множество X конечно или счётно
- целочисленные --

- булевы --

- непрерывные --

- бесконечномерные
- функциональные
Задачи оптимизации бывают:
- условные --
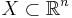
- безусловные --

Классификация по свойствам целевой функции: выпуклость, гладкость и т.п.
Классификация по результату:
- локальная оптимизация
- глобальная оптимизация
Выпуклое множество (вики) -- такое множество, которое содержит вместе с любыми двумя своими точками еще и отрезок, их соединяющий.
Функция f называется выпуклой, если её надграфик (множество точек над графиком: 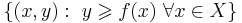 ) является выпуклым множеством.
) является выпуклым множеством.
Утверждение. Любая точка локального минимума выпуклой функции является точкой её глобального минимума.
Преимущества выпуклых задач:
- применим метод эллипсоидов, причем сложность - полиномиальна
- для острых задач (целевая функция убывает в окрестности минимума не медленнее некоторой линейной функции) можно получить точное решение
[править] Формула градиентного метода в задаче безусловной минимизации
Методичка. стр 41-42
Основная идея:
- берем некоторое начальное значение
- итеративно вычисляем градиент целевой функции
- двигаемся в обратном направлении
- и так постепенно приходим к (локальному) минимуму функции
Формула градиентного метода -- xt + 1 = xt − αtgradf(xt), где αt -- шаговый множитель:
- пассивный способ: {αt} выбирается заранее
- адаптивный способ: {αt} выбирается в зависимости от реализующейся xt
- метод скорейшего спуска --
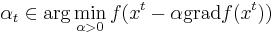
- метод дробления (деления пополам) -- если f(xt + 1) > f(xt), то возвращаемся к шагу t с новым значением αt = αt / 2
- метод скорейшего спуска --
[править] Идея метода Ньютона
Методичка, стр. 43
Метод ньютона -- это фактически градиентный спуск с адаптивыным коэффициентом, который берется, как 2 производная целевой функции.
Реально можно вывести формулу Ньютона из разложения по Тейлору до 2 производной в окрестности точки минимума.
[править] Формула метода Ньютона в задаче безусловной минимизации
Методичка. стр 43
Формула Ньютона -- 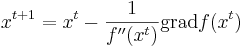 , при этом начальное приближение должно находиться достаточно близко к искомой точке минимума.
, при этом начальное приближение должно находиться достаточно близко к искомой точке минимума.
Метод ньютона имеет квадратичную скорость сходимости: 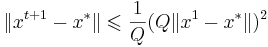 , где Q - некоторая константа
, где Q - некоторая константа
Ограничения:
- невырожденность матрицы 2 производных (гессиана)
- близость начального приближения к точке минимума (
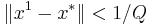 )
)
[править] Идея метода штрафов
Методичка. стр 44
Смысл метода в том, чтобы свести задачу условной оптимизации к задаче безусловной оптимизации, то есть избавится от ограничения на область, в которой ищем минимум.
Для этого вводится так называемая функция штрафа, которая равна нулю в той области, в которой мы "условно оптимизируем" целевую функцию, а в остальных точках добавляет к значению целевой функции некоторое значение (собственно, штраф).
Пример. Пусть область задаётся следующим образом: 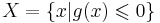 , где g(x) -- некоторая функция. Тогда рассмотрим задачу безусловной минимизации целевой функции f(x) со штрафом:
, где g(x) -- некоторая функция. Тогда рассмотрим задачу безусловной минимизации целевой функции f(x) со штрафом: 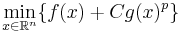 , где C -- некоторая константа [??], а
, где C -- некоторая константа [??], а 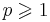 -- параметр штрафа
-- параметр штрафа
[править] Способы решения переборных задач
[править] Методы глобальной минимизации
Методичка. стр. 52 (52-55)
[править] Метод ветвей и границ для глобальной минимизации Липшицевых функций
Методичка. стр. 54
[править] Метод ветвей и границ для ЦЛП. Различные стратегии метода
Методичка. стр. 57
[править] Идея метода ветвей и границ. Пример для задачи БЛП
Методичка. стр. 59
[править] Теорема оптимальности для разложимых функций
Методичка. стр 60
Опр. Функция f называется разделяемой на f1 и f2, если она представима в виде f(x,y) = f1(x,f2(y)).
Опр. Функция f называется разложимой на f1 и f2, если:
- она разделяема на f1 и f2
- f1 монотонно не убывает по последнему аргументу
Теорема оптимальности для разложимых функций: minx,y(f(x,y)) = minx(f1(x,miny(f2(y)))).
Указанная теорема используется для уменьшения размерности оптимизационных задач и в методе ДП.
[править] Применение метода динамического программирования для понижения размерности разложимой оптимизационной задачи
Методичка. стр. 62
[править] Метод динамического программирования для БЛП с неотрицательными коэффициентами
Методичка. стр. 63-64
[править] Неотсортировано
- Полиномиальный алгоритм округления ε1-приближенного решения системы линейных неравенств
- Понятие о временной сложности алгоритмов
- Понятие о недетерминированно-полиномиальных задачах
- Оценка сложности метода эллипсоидов ε2-приближенного решения озЛП