Методы оптимизации, определения
Материал из eSyr's wiki.
[править] Лекция 1
Решить задачу оптимизации — не значит, что нужно решить конкретную задачу, типа «посчитать высоту Университета», это значит написать программу решения определённого класса задач.
Массовая задача — набор, класс индивидуальных задач (I), П = {I}. Индивидуальная задача получается из массовой путём конкретизации. То есть, у массовой задачи есть свободные параметры.
Алгоритм (А) — программа для машины Тьюринга.
П — задача распознавания свойств, если в качестве требования к решению является ответ «да» или «нет».
Алфавит Σ — множество, состоящее из конечного числа символов 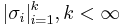
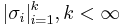
Слово — конечный набор букв, слово будем обозначать &sigma = {σi, σj, σk, …}
Схема кодирования (кодировка) — e: П → Σ*, ∀I ⇒ e(I) = σ ∈ Σ* — отображение массовой задачи в множество слов, индивидуальная задача отображается в слово.
Язык — множество слов, соответствующих правильным решениям: L(Π, e) = у(Н) = {σ ∈ Σ* | Σ — алфавит e, σ = e(I), I ∈ Y}
Определение 1. A решает задачу П с кодировкой e, если язык алгоритма совпадает с задачей П в кодировке E: L(A) = L(Π, e), и для любого слова из их множества алгоритм останавливается: ∀ σ ∈ Σ* A(σ) останавливается
Определение 2. Временна'я сложность алгоритма A решения задчи П — функция TA(.): TA = 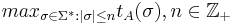
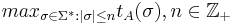
Определение 3. Класс полиномиально разрешимых задач 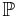 = {L(Π, e) | ∃ A решающий Π с кодировкой e, ∃p(.) — полином:
= {L(Π, e) | ∃ A решающий Π с кодировкой e, ∃p(.) — полином: 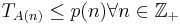
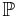 = {L(Π, e) | ∃ A решающий Π с кодировкой e, ∃p(.) — полином:
= {L(Π, e) | ∃ A решающий Π с кодировкой e, ∃p(.) — полином: 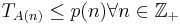
Труднорешаемые задачи — задачи, для которых нет полиномиального алгоритма.


