Методы оптимизации, 02 лекция (от 15 февраля)
Материал из eSyr's wiki.
//отсутствует первая половина лекции
Утверждение 0. P ⊂ NP.
Основной вопрос — вопрос строгого включения. Не удоаётся доказать ни то, что P строго включается в NP, ни то, что он равен NP. Сейчас господствует гипотеза строгого включения, но не исключено и обратное.
Прдположение о том, что у нас имеется строгое включение... мы хотим определить те задачи, котрые в случае строгого включения не попадут в класс P. Для того, чтобы ввести такие здаачи, нам понадобится понятие «одна задача сложнее другой». Например: за полиномиальное время из алгоритма решения первой задачи можно а полин. время получить второй, или привести алгоритм решения первой к алгоритму решения второй
Опрееделение 6. Массовая задача распознавания свойств П' с кодировкой e' полиномиально сводится к П с e, если у нас Невозможно разобрать выражение (неизвестная ошибка): \exist f: e'(\Pi') \darr e(\Pi)<math>, это значит, что <math>f(e'(Y')) = e(Y)<math> и существует детерминированная МТ A<sub>f</sub>, которая реализует f за полиномиальное время. Далее будем писать <math>\Pi' \profto(?) \Pi
(значёк бесконечности с отгрызенной правой частью) --- полиномиальная сводимость
Этот значёк можно воспринимать как знак нестрогого порядка.
Утверждение 2. Если П1 сводится к П2 и П2 к П3, то (транзитивность сводимости) П1 сводится к П3
Доказательство основано на том, что полином от полинома — полином.
Утв. 3. Если П' полиномиально сводится к П и П ∈ P, то П' ∈ P.
Доказательство. 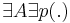 . Построим алгоритм A', решающий задачу П': Невозможно разобрать выражение (неизвестная ошибка): A' = A \times A_f I' \in \Pi' \overbrace{\rArr}{A_f} I \in \Pi {overbrace}{\dArr}{A} </amth> решение, <math>t_{A'}(I') \le p(P_f(|I|))
.
. Построим алгоритм A', решающий задачу П': Невозможно разобрать выражение (неизвестная ошибка): A' = A \times A_f I' \in \Pi' \overbrace{\rArr}{A_f} I \in \Pi {overbrace}{\dArr}{A} </amth> решение, <math>t_{A'}(I') \le p(P_f(|I|))
.
Соврешенно аналогично получаем
Утверждение 4. Если П' полиномиально сводится к П и П ∈ NP, то П' ∈ NP.
Доказательство аналогично.
Основное определение всей теории сложности:
Определение 7. Массовая задача П называется NP-полной, или, иначе, универсальной, обозначение NPC (NP-complete), если
- П ∈ NP
- ∀ П ∈ NP ⇒ П' сводится к П
С определения этого класса пошла теория сложности как теория, и основной теоремой теории сложности является теорема Кука (1971 год):
Теорема Кука (Cook, 1971) NPC ≠ ∅
В частности, задача выполнимости (ВЫП) принадлежит NPC
Эта теорема будет доказываться на 5 курсе.
ВЫП: ∃ выполняющий набор для КНФ?
Невозможно разобрать выражение (неизвестная ошибка\Or): \And_{i=1}^{N} D_i(z), D_i(z) = \Or_{j = 1}^{n_j} z_j^(\alpha_j), z_j^0 = \empty, z_j^1 = z_j, z_j^{-1} = \not z_j
Соответственно, задача состоит в ∃ z: КНФ(z) = 1.
Утверждение. ВЫП ∈ NP
Доказательство. Предположим, что ответ да. Тогда &exists;z с волной, КНФ(z с волной) = 1. Для проверки надо подстваить аргумент в КНФ, что все дизьюнкты равны 1, проверка имеет линейную сложность, проверка полиномиальная.
Почему так хороши, важны, интересны NP-полные задачи?
Утверждение 5. Если P ∩ NPC ≠ ∅ ⇒ P = NP, и наоборот, если найдётся П такая, что П ∈ NPC \ P, то NPC &subb; NP \ P
В книге Грея-Джонсона приведено более 500 задач из класса NPС, и все задачи остальные, их принадлежность к классу NPC доказывалась не напрямую, а доказывалась на основании следующего критерия:
Теорема (критерий NP-полноты). Массовая задача П распознавания свойств ∈ NPC ⇔
- П ∈ NP
- ∃ П* ∈ NPC, П* полиномиально сводится к П.
Доказательство (по транзитивности). ∀ П' ∈ NP, П' полиномильано сводится к П* полиномиально сводится к П.
Утвеждение. БЛН (задача булевых линейных неравенств) ∈ """NPC
Доказательство. ВЫП сводится к БЛН
Задача БЛН: Невозможно разобрать выражение (неизвестная ошибка): \exist z \in \mathbb{B}^n (система) a_11 z_1 + ... + a_1n z_n \le b_1\ ...\ a_m1 z_1 + ... + a_mn z_n \le b_m
эквивалентная проверка: z_1 \or \not z_2 \or z_4 || z_1 + (1 - z_2) + z_4 \ge 1
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15
Календарь
| пт | пт | пт | пт | пт | |
Февраль
| 08 | 15 | 22 | 29 | |
Март
| 06 | 13 | 20 | 27 | |
Апрель
| 04 | 11 | 18 | 25 | |
Май
| 02 | 16 | 23 |
Материалы
Упражнения
||
Задачи | Определения | Утверждения | Теоремы
||
Теормин | Обозначения


