ОКФиКВ, 03 лекция (от 27 февраля)

Материал из eSyr's wiki.

(Различия между версиями)

Версия 07:50, 4 апреля 2008

Диктофонная запись второй части лекции: http://esyr.org/lections/audio/quantphys_2008_summer/QP_08_02_27.ogg Лекция 3.

Темы

Финитные и инфинитные движения. Дискретные и непрерывные энергетические спектры. Движение частицы в одномерной потенциальной яме. Дискретность энергетических спектров. Приближение двухуровневой системы. Эффект тунелирования через барьер. Движение в периодическом потенциальном поле.

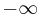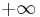Если движение совершается без граничных условия (т.е. от $-\infty$ до $+\infty$ ) то движение называется инфинитным. Если движение происходит в ограниченной области, то движение финитно.

Примеры:

Свободное движение.

Потенциальная энергия $U = c o n s t$ . Положим $U = 0$ .

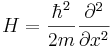
$H=\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}$

Уравнение Шредингера:

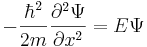$-\frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial x^2}=E\Psi$ (это частный случай уравнения Шреднигера!)

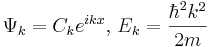
$\Psi_k=C_ke^{ikx},\,E_k=\frac{\hbar^2k^2}{2m}$

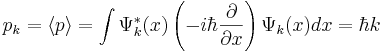
$p_k = \langle p\rangle = \int\Psi^*_k(x)\left(-i\hbar\frac{\partial}{\partial x}\right)\Psi_k(x)dx=\hbar k$

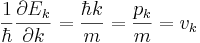$\frac{1}{\hbar}\frac{\partial E_k}{\partial k}=\frac{\hbar k}{m} = \frac{p_k}{m} = v_k$ Эта формула верна и в общем случае (без доказательства).

В прямоугольной потенциальной яме

(см. картинку на первой фотографии доски)

Впервые мы сталкиваемся со случаем финитного движения.

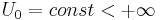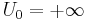При $U_0 = const < +\infty$ получаем сложную математическую задачу. Мы будем рассматривать случай $U_0 = +\infty$ .

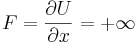$F=\frac{\partial U}{\partial x} = +\infty$ Слева и справа действуют бесконечные силы, не выпускающие частицу из ямы.

Мы должны поставить математические условия к тому, что частица не проникает сквозь стенки ямы. $Ψ( - a / 2) = Ψ(a / 2) = 0$ . Посмотрим, какой спектр получается в этом случае. Теперь мы должны решать уравнение Шредингера. У нас здесь три области. Когда решается задача с конечной глубиной, трудность в решении для каждой области, а потом сшивать их. Тут проще потому, что в области 1 и 3 ... равно 0. А в области 2 случай ничем не отличается от свободного движения чатицы. В области 1 и 3 волновая функция 0, а в области 2 это 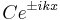$Ce^{\pm ikx}$ . Тогда получается вот какая картина: надо брать суперпозицию этих функций. Частным решением является каждая из функций, общим решением является супрерпозиция функций:

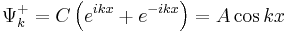$\Psi_k^+=C\left(e^{ikx}+e^{-ikx}\right)=A\cos{kx}$ (решение должно быть действительным)

Но есть ещё одно решение:

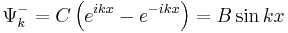
$\Psi_k^-=C\left(e^{ikx}-e^{-ikx}\right)=B\sin{kx}$

Чему равняется k? Лектор ещё раз запишет уравнение Шредингера в области 2, и теперь он просто подставляет $C e i k x$ .

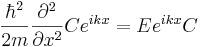
$\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}Ce^{ikx}=Ee^{ikx}C$

k зависит от энергии. Если энергия задана, то 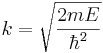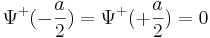$k = \sqrt{\frac{2mE}{\hbar^2}}$ . $\Psi^+(-\frac{a}{2})=\Psi^+(+\frac{a}{2})=0$ Граничные условия у нас 0, значит, cos обращается в 0 здесь, здесь, и 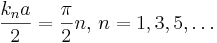$\frac{k_na}{2}=\frac{\pi}{2}n,\,n=1,3,5,\dots$ . Соответственно, cos обращается в 0 в дискретных точках. То есть, мы получаем квантование вектор k в результате граничных условий. Не все значения удовл граничным условиям, отсюда и получается квантование. Каждому этому значению k соответствует энергия, получаем квантованный спектр энергий, в данном случае дискретный квантованный спектр энергий.

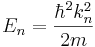
$E_n=\frac{\hbar^2k_n^2}{2m}$

Чтобы сделать заключение, исследуем второй случай.

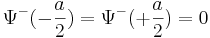
$\Psi^-(-\frac{a}{2})=\Psi^-(+\frac{a}{2})=0$

Ставим граничное условие, равенство к 0 на границе, опять же приводит к квантованию вектора k:

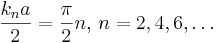
$\frac{k_na}{2}=\frac{\pi}{2}n,\,n=2,4,6,\dots$

Теперь мы можем резюмировать наши результаты. Наличие гр. условий приводит к дискр. энерг. спектру и дискр. набору волновых функций. Лектор их выпишет: ... . Вот результат мат. иссл. --- решения ур. Ш. Каки реузльтаты получаем: интересный эффект --- квантовый параллелизм. Он явл. следвтвием принципа суперпозиции. В обычной механике шар может лететь либо вперёд, либо назад. А в квантовой механике мы имеем решение: ... --- две волны, напр. противоположно друг другу. Но мы же стационарное решение нашли. А если подставить общее? Какой вид будет иметь полное решение тогда? ... Тогда ясно, что эти 2 волны распространяются в разных нпр. Фиксируете фазу, ддиф. по t, и получаете: ... . Мы впервые столкнулись с квантовым параллелизмом, в котором частица обл. обпр. импульсом. Это суперпозиц. сост. Характеристики суперпозиц. сост. неопределены. Нарисуем график: просто косирнус, n=2, первое возб. сост., это неч. функция. И, соответственно, уровни энергии: .... . И дальше, по мере возрастания n, дальше мы получаем, что уровни расходятся, E_n ~ n^2, следовательно, расстояние пропорционлаьно n. Что главное: энерг. спектр при наличии гранич условий становится дискретным. В квантовой механике получаем дискр. сост., и благодаря этому возм. квантовые вычисл. Интуиция подск., что чтобы реализ бит, нужна система с двумя состояниями. Если оставим два уровня, то это и есть кубит. Но есть отличие: он может находиться в суперпозиционном состоянии, давая экспоненциально большой выигрыш, и преимущества квантового компьютинга сидят в самой квантовой механике. В классической механике непр. энергетический спектр. А где появляются обертона? Серипач изм. длину волны, изменяется звучания. Изменяются гранич. условия. Гранич. условия приводят к квантованию. k квантовано, может принимать разреш знач, и екаждому значению k соответствует свой уровень энергии e_n. Дискр. энерг. спектр. Будет ещё один --- зонный спектр.

Теперь качественно обсудим те изменения, которые произойдут в случае реальной ямы. У нас есть аппарат, и даже не решая, мы можем сделать выводы. С чего начинаем: с записи гамильтониана. В области 2 ничего не меняется, уравнение Ш. такое же. А теперь в области 3: в обл. 3 нужно u_0 учесть, и получаем: ... . Теперь, какое соотношение между u_0 и e? Нас будет интересовать связанное движение, и каждый ответит, что e < u_0? ЧТОбЫ ДВИжЕНИЕ бЫЛО СВЯЗНЫМ. ... Это означает, что у нас есть две возможности, два решения. Какое выбрать из этих двух решений? Ясно, что убывающее, возрастающее не удовлетворяет условиям нормировки. Обсудим физический смысл. ... Это область, в которой полная энергия меньше, че мпотенциальная. Внутри ямы, наоборот: ... . Но вне ямы e < u_0. Это невозможно в классической физике. Поскольку к полной энергии добавляется положительно опр. форма. Эта область называется ... . Квантовая частица может проникать в классич. недоступную область. Это качественный вывод. Какое следствие отсюда: несколько видоизменённых задач. ... Летит частица, волна слева направо. И вот частица попадает вот в эту область, а это энергия частицы, e < u_0. В некотором смылсе это аналог классической задачи: катится шарик со скоростью v, масса m, высота h. вопрос, что произойдёт? Как решать в классич. случае, понятно: сравнить кин. и пот. энергию. В квантовом случае оказывается, что частица проходит через этот барьер (туннелирует), с определённой вероятностью отражается. Мы не найдём точно туннелирование, мы найдём экспоненциальный фактор. ... Это и будет вероятность просачивания/прохождения/туннелирования. Эффект туннелирования очень часто встречается в физике. При распаде идёт эффект туннелирования. Мы дома сталкиваемся с эффектом туннелирования. Например, если мы имеем контакт двух проводов. Электроны встречают слой диелектрика, и туннелируют. При этом возрастают примеры и сопротивление. Это простейжий пример эффекта туннелирования.

Осталось полчаса, и лектор хотел бы перейти к движению частицы в периодическом потенциале, но сначала лектор устроит проверочку.

Очень интересный и важный тип движкения. Предыдущий тип движения тоже очень важный тип, как пример --- движение электрона в атоме, там кулоновская яма. Тут жен примером является движение электрона в кристалле.

Ничего нового в подходе не езобретаем и изобрести не можем, действуем по схеме. КМ --- набор рецептов. Вот мы решили уравн Ш., и говорим, волна бежит сюда, волна бежит сюда, берём суперпозицию. Но где масса электрона? На этот вопрос КМ не отвечает, в первом постулате говорится. Это не вопрос КМ, КМ его отметает. Ни наа что другое КМ не претендует. Это от\дна из причин, по которой многие не удовлетворены КМ.

Ставим задачу. Есть у нас кристалл --- периодическое чередование атомов. Вообще, там трёхмерное движение, но мы рассм. одномер. движение. Получается такой одномерный кристалл. Ионы в кристалле создают периодический потенциал u(x). Главное что --- при приближении электрона к ядру его потенциал уменьшается. Важным оказывается только одно обстоятельство: периодичность движения. И мы отражаем эту периодичность такой формулой: ... . Эта функция, которая вляется периодической, может быть разложена в ряд Фурье таким образом ... . Вот всё, что мы можем. А, мы ещё можем записать гамильтониан: ... . Это довольно сложная задача. Но в общем виде можно получить качественное решение. Как мы будем рассуждать? Представьте: кристалл, периодическая структура, влетает в кристалл волна. Что будет происходить с волной, когда она входит в период. структуру. Тот, кто изучал волну, скажет, что происходит дифракция, рождаются дифрагированные волны. Вот это и будет волновое поле электрона в кристалле. Построим волновой пакет --- сумму волн. Теперь у нас есть решение: ... . Леткор просто подставил разложение потенциала в уравнение. Отсаётся вопрос, что такое ek' --- это энергия возмущённого электроном кристалла (?). Теперь преобразуем его следующим образом --- умножим на e^-ikx и проинтегрируем. ЛЕктор запишет результат: ... . Что же отсюда следует: если мы запускаем волну, то в результате дифракции появляются дифрагированные волны, сдвинутые на некоторую обратную решётку. Это означает, что в этом пакете не будет никаких волн кроме исходных волн и сдвинутых. Только такие волны должны фигурировать в пакете. Давайте запишем этот волновой пакет. ... . Это и есть решение ур. Ш. Конечно, мы его не решили, мы предугадали форму. Но так оно и есть. Придадим ему канонический вид. ... Это и есть решение решение ур. Ш. Это волна, аплитуда которой промодулирована. Какими свойствами она обладает:

... явл. периодической функцией с периодом решётки
... явл. периодической функцией ....

Функция ψk называется функцией Блоха или блоховской функцией. Этот результат явл. сутью теоремы Блоха: волна в кристале имеет блоховский вид

Основы квантовой физики и квантовых вычислений

01 02 03 04 05 06 07 08 09 10 11 12

Календарь

Февраль	13	20	27
Март	05	12	19	26
Апрель	02	09	16	23	30

Эта статья является конспектом лекции.

Эта статья ещё не вычитана. Пожалуйста, вычитайте её и исправьте ошибки, если они есть.

Получено с http://esyr.org/wiki/%D0%9E%D0%9A%D0%A4%D0%B8%D0%9A%D0%92%2C_03_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D1%8F_%28%D0%BE%D1%82_27_%D1%84%D0%B5%D0%B2%D1%80%D0%B0%D0%BB%D1%8F%29

Категории: ОКФиКВ | Лекции | Незавершённые статьи

@@ Строка 1: / Строка 1: @@
 '''Диктофонная запись второй части лекции:''' http://esyr.org/lections/audio/quantphys_2008_summer/QP_08_02_27.ogg
+Лекция 3.
+Темы
+* Финитные и инфинитные движения. Дискретные и непрерывные энергетические спектры. Движение частицы в одномерной потенциальной яме. Дискретность энергетических спектров. Приближение двухуровневой системы. Эффект тунелирования через барьер. Движение в периодическом потенциальном поле.
+Если движение совершается без граничных условия (т.е. от <math>-\infty</math> до <math>+\infty</math>) то движение называется инфинитным. Если движение происходит в ограниченной области, то движение финитно.
+''Примеры'':
+* Свободное движение.
+Потенциальная энергия <math>U=const</math>. Положим <math>U=0</math>.
+<math>H=\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}</math>
+Уравнение Шредингера:
+<math>-\frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial x^2}=E\Psi</math> (''это '''частный''' случай уравнения Шреднигера!'')
+<math>\Psi_k=C_ke^{ikx},\,E_k=\frac{\hbar^2k^2}{2m}</math>
+<math>p_k = \langle p\rangle = \int\Psi^*_k(x)\left(-i\hbar\frac{\partial}{\partial x}\right)\Psi_k(x)dx=\hbar k</math>
+<math>\frac{1}{\hbar}\frac{\partial E_k}{\partial k}=\frac{\hbar k}{m} = \frac{p_k}{m} = v_k</math> Эта формула верна и в общем случае (без доказательства).
+* В прямоугольной потенциальной яме
+(см. картинку на первой фотографии доски)
 Впервые мы сталкиваемся со случаем финитного движения.
-Мы должны поставить мат. условия к тому, что частица не проникает сквозь стенки ямы. &xi;(-x/2) = &xi;(x/2) = 0. Посмотрим, какой спектр получается в этом случае. Теперь мы должны решать уравнение Ш.. У нас здесь три области. Когда решается задача с конечной глубиной, трудность в решении для каждой области, а потом сшивать их. Тут проще потому, что в области 1 и 3 ... равно 0. А в области 2 случай ничем не отл. от свободного движения чатицы. В области 1 и 3 волновая функция 0, а в области 2 это Ce<sup>+/- ikx</sup>. Тогда получается вот какая картина: надо брать суперпозицию этих функций. Частным реш. явл. каждая из функций, общим решением решается супрерпозиция функций. ... Но есть ещё одно решение: ... . Чему равняется k? Лектор ещё раз запишет уравнение Ш. в области 2, и теперь он просто подставляет Ce<sup>ikx</sup>. Ну и так далее. k зависит от энергии. Если энергия задана, то k = sqrt(2me/h). ... Граничные условия у нас 0, значит, cos обращается в 0 здесь, здесь, и ... . Соответственно, cos обращается в 0 в дискретных точках. То есть, мы получаем квантование векторf k в рез-те граничных условий. Не все знач. удовл гранич. условиям, отсюда и получается квантование. Каждому этому значению k соответствует энергия, получаем квантованный спектр энергий, в данном случае дискр. кв. спектр энергий. Чтобы сделать заключение, исследуем второй случай. ... Ставим граничное условие, равенство к 0 на границе, опять же приводит к квантованию вектора k, и теперь такое квантование: &pi;/2 n, n --- чётное.
+При <math>U_0 = const < +\infty</math>получаем сложную математическую задачу. Мы будем рассматривать случай <math>U_0 = +\infty</math>.
+<math>F=\frac{\partial U}{\partial x} = +\infty</math> Слева и справа действуют бесконечные силы, не выпускающие частицу из ямы.
+Мы должны поставить математические условия к тому, что частица не проникает сквозь стенки ямы. <math>\Psi(-a/2) = \Psi(a/2) = 0</math>. Посмотрим, какой спектр получается в этом случае. Теперь мы должны решать уравнение Шредингера. У нас здесь три области. Когда решается задача с конечной глубиной, трудность в решении для каждой области, а потом сшивать их. Тут проще потому, что в области 1 и 3 ... равно 0. А в области 2 случай ничем не отличается от свободного движения чатицы. В области 1 и 3 волновая функция 0, а в области 2 это <math>Ce^{\pm ikx}</math>. Тогда получается вот какая картина: надо брать суперпозицию этих функций. Частным решением является каждая из функций, общим решением является супрерпозиция функций:
+<math>\Psi_k^+=C\left(e^{ikx}+e^{-ikx}\right)=A\cos{kx}</math> (решение должно быть действительным)
+Но есть ещё одно решение:
+<math>\Psi_k^-=C\left(e^{ikx}-e^{-ikx}\right)=B\sin{kx}</math>
+Чему равняется k? Лектор ещё раз запишет уравнение Шредингера в области 2, и теперь он просто подставляет <math>Ce^{ikx}</math>.
+<math>\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}Ce^{ikx}=Ee^{ikx}C</math>
+k зависит от энергии. Если энергия задана, то <math>k = \sqrt{\frac{2mE}{\hbar^2}}</math>. <math>\Psi^+(-\frac{a}{2})=\Psi^+(+\frac{a}{2})=0</math> Граничные условия у нас 0, значит, cos обращается в 0 здесь, здесь, и <math>\frac{k_na}{2}=\frac{\pi}{2}n,\,n=1,3,5,\dots</math>. Соответственно, cos обращается в 0 в дискретных точках. То есть, мы получаем квантование вектор k в результате граничных условий. Не все значения удовл граничным условиям, отсюда и получается квантование. Каждому этому значению k соответствует энергия, получаем квантованный спектр энергий, в данном случае дискретный квантованный спектр энергий.
+<math>E_n=\frac{\hbar^2k_n^2}{2m}</math>
+Чтобы сделать заключение, исследуем второй случай.
+<math>\Psi^-(-\frac{a}{2})=\Psi^-(+\frac{a}{2})=0</math>
+Ставим граничное условие, равенство к 0 на границе, опять же приводит к квантованию вектора k:
+<math>\frac{k_na}{2}=\frac{\pi}{2}n,\,n=2,4,6,\dots</math>
 Теперь мы можем резюмировать наши результаты. Наличие гр. условий приводит к дискр. энерг. спектру и дискр. набору волновых функций. Лектор их выпишет: ... . Вот результат мат. иссл. --- решения ур. Ш. Каки реузльтаты получаем: интересный эффект --- квантовый параллелизм. Он явл. следвтвием принципа суперпозиции. В обычной механике шар может лететь либо вперёд, либо назад. А в квантовой механике мы имеем решение: ... --- две волны, напр. противоположно друг другу. Но мы же стационарное решение нашли. А если подставить общее? Какой вид будет иметь полное решение тогда? ... Тогда ясно, что эти 2 волны распространяются в разных нпр. Фиксируете фазу, ддиф. по t, и получаете: ... . Мы впервые столкнулись с квантовым параллелизмом, в котором частица обл. обпр. импульсом. Это суперпозиц. сост. Характеристики суперпозиц. сост. неопределены. Нарисуем график: просто косирнус, n=2, первое возб. сост., это неч. функция. И, соответственно, уровни энергии: .... . И дальше, по мере возрастания n, дальше мы получаем, что уровни расходятся, E<sub>n</sub> ~ n^2, следовательно, расстояние пропорционлаьно n. Что главное: энерг. спектр при наличии гранич условий становится дискретным. В квантовой механике получаем дискр. сост., и благодаря этому возм. квантовые вычисл. Интуиция подск., что чтобы реализ  бит, нужна система с двумя состояниями. Если оставим два уровня, то это и есть кубит. Но есть отличие: он может находиться в суперпозиционном состоянии, давая экспоненциально большой выигрыш, и преимущества квантового компьютинга сидят в самой квантовой механике. В классической механике непр. энергетический спектр. А где появляются обертона? Серипач изм. длину волны, изменяется звучания. Изменяются гранич. условия. Гранич. условия приводят к квантованию. k квантовано, может принимать разреш знач, и екаждому значению k соответствует свой уровень энергии e_n. Дискр. энерг. спектр. Будет ещё один --- зонный спектр.

ОКФиКВ, 03 лекция (от 27 февраля)

Материал из eSyr's wiki.

Версия 07:50, 4 апреля 2008

Просмотры

Личные инструменты

Навигация

инструменты

Разделы

Спецкурсы

9 семестр

7 семестр

5 семестр

3 семестр

Поиск

Инструменты