ОКФиКВ, 02 лекция (от 20 февраля)

Материал из eSyr's wiki.

(Различия между версиями)

Текущая версия

Лекция номер 2

Темы:

Принцип суперпозиции. Соотношение неопределённостей. Операторы физич. величин. Уравнение Шредингера.

Сменили парадигму и приняли волновую прадигму под давлением эксперимента.

Если частица имеет импульс p, то волна, которая описывает эту частицу, записывается уравнением де Бройля $Ψ k (x) = C e i k x - i ω t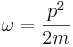$ , $\omega = \frac{p^2}{2m}$ .

Кроме этого, под давлением эксперимента приняли статистическую интерпритацию волновой функции $Ψ(x, t)$ . Поскольку $| Ψ | 2$ --- плотность вероятности, то интеграл этой функции по всей области x равен 1.

∫	\| Ce^{ikx − iωt} \| ²dx = 1
x

Какова же вероятность обнаружить частицу в момент t в точке x? Для этого берём функцию и находим квадрат модуля. Отсуда получаем, что плотность вероятности --- константа. Это означает, что частица полностью делокализована. Что это за частица? Это частица, у которой импульс полностью задан. Мы получили частный случай общего соотношения неопределенности Гейзенберга. Мы получим общее соотношение Гейзенберга, и увидим, что так и есть. Сейчас мы это соотношение получим в некоем простом случае.

Но прежде сформулируем принцип суперпозиции. Если спросим, в чём преимущество квантовых приборов? Ответ: в принципе суперпозиции. Квантовый компьютер работает параллельно, на одном процессоре осущ. N операций благодаря приныципу суперпозиции. Лектор будет указ. на принц. суперпоз. в разных задачах и мы увидим, что весь микромир основывается на нём, множество эффектов...

Сформулируем принцип суперпозиции: если квантовая частица может находиться в состоянии $Ψ 1 (x, t)$ , в состоянии $Ψ 2 (x, t)$ , то он может находиться в состоянии $Ψ(x, t) = C 1 Ψ 1 (x, t) + C 2 Ψ 2 (x, t)$ .

Теперь приступим к выводу соотношения неопределенности Гейзенберга. В состоянии, заданном k мы знаем импульс. А если рассмотрим суперпозицию, то импульс не будет определен, с какой точностью мы сомжем знать положение? Мы будем использавать принцип суперпозиции в след виде:

Ψ =	∑	c_nΨ_n
	n

. Рассмотрим интеграл

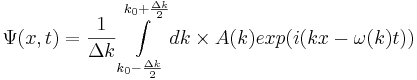
$\Psi(x, t) = \frac{1}{\Delta k} \int\limits_{k_0 - \frac{\Delta k}{2}}^{k_0 + \frac{\Delta k}{2}} dk \times A(k)exp(i(kx-\omega(k)t))$

Это сумма различных волн де Бройля с различными $k$ , а частоты, в силу их различия, зависят от $k$ . Эти $k$ группируются вокруг $k 0$ . Волновой пакет называется узким пакетом, если $Δ k < < k 0$ . Тогда получим:

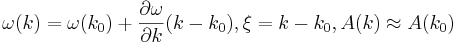
$\omega(k) = \omega(k_0) + \frac{\partial\omega}{\partial k}(k-k_0), \xi = k-k_0, A(k)\approx A(k_0)$

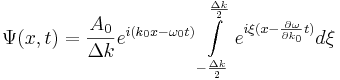
$\Psi(x,t)=\frac{A_0}{\Delta k}e^{i(k_0x-\omega_0t)}\int\limits_{-\frac{\Delta k}{2}}^{\frac{\Delta k}{2}}e^{i\xi(x-\frac{\partial\omega}{\partial k_0}t)}d\xi$

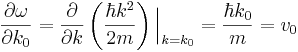
$\frac{\partial\omega}{\partial k_0}=\frac{\partial}{\partial k}\left(\frac{\hbar k^2}{2m}\right)\Bigr|_{k=k_0}=\frac{\hbar k_0}{m} = v_0$

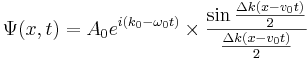
$\Psi(x,t)=A_0e^{i(k_0-\omega_0t)}\times\frac{\sin\frac{\Delta k(x-v_0t)}{2}}{\frac{\Delta k(x-v_0t)}{2}}$

Вот перед нами этот волновой пакет. Чтобы увидеть суть, упростим обозначения: 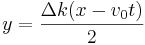$y=\frac{\Delta k(x-v_0t)}{2}$

И тогда наш волновой пакет приобретает такой вид:

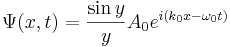
$\Psi(x,t)=\frac{\sin y}{y}A_0e^{i(k_0x-\omega_0t)}$

у него есть промодулированная амплитуда 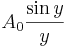$A_0\frac{\sin y}{y}$ , а остальное --- волна де Бройля.

Максимум вероятности движется со скоростью $v 0$ --- скорость центарального компонента волнового пакета.

Импульс оперделён с точностью $Δ k$ , и неопределённость координаты: ...

Выразим это соотношение математически и получим отношение неопределённости.

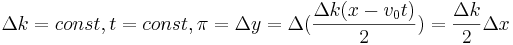
$\Delta k = const, t = const, \pi = \Delta y = \Delta (\frac{\Delta k (x - v_0 t)}{2}) = \frac{\Delta k}{2}\Delta x$

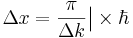
$\Delta x = \frac{\pi}{\Delta k}\bigr|\times\hbar$

В результате получаем: 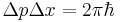$\Delta p \Delta x = 2\pi\hbar$

Отсюда получаем: если $Δ p$ положить равным 0, то получаем одну волну де Бройля, но тогда координата неопределена. Аналогично с точным заданием $Δ x$ . Как задать $Δ x$ равным 0? Задать бесконечно большой волновой пакет, тогда получим интеграл, который является дельта-функцией.

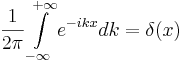
$\frac{1}{2\pi}\int\limits_{-\infty}^{+\infty}e^{-ikx}dk=\delta(x)$

Точное соотношение Гейзенберга записывается так:

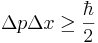
$\Delta p\Delta x \ge \frac{\hbar}{2}$

Можно записать соотншение неопределенности Гейзенберга в операторном виде.

В классической механике частица имеет траекторию, и пара (p, x) точно задана. В квантовой (волновой) механике утверждается, что есть некая область.

[править] Операторы квантовой механики

Вопросы, которые входят в критерии.

Первый постулат. Квантовый объект описывается с наибольшей полнотой волновой функцией.

Второй постулат. Каждой классической физической величине соответствет оператор. Значению физической величины, измеряемой в эксперименте, соответствует среднее значение оператора этой физической величины.

Постулат утверждает, что если мы строим теорию квантового объекта, то мы должны отталкиваться от классических физических величин. Хотя мы увидим, что это не всегда так, например, спин. Вообще, спин --- объект релятивистской квантовой механики, а в нерелятивистской мы должны отталкиваться от классических величин.

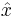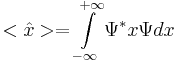
Координата. Оператор координаты $\hat x$ --- сама координата, умножение на x. $<\hat x> = \int\limits_{-\infty}^{+\infty}\Psi^*x\Psi dx$

$Ψ *$ --- комплексное сопряжение., интеграл по всей прямой &ksi;*x&ksi;dx = интеграл по всей прямой |&ksi;|^2 x&ksi;dx

f(x), 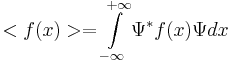$<f(x)> = \int\limits_{-\infty}^{+\infty}\Psi^*f(x)\Psi dx$

Оператор импульса. Операторы импульса выглядит так:

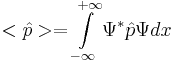
$<\hat p> = \int\limits_{-\infty}^{+\infty}\Psi^*\hat p\Psi dx$

из каких соображений мы можем получить это: из волны де Бройля. При рассмотрении волны де Бройля мы считаем, что импульс задан, и его значение --- среднее значение. 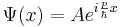$\Psi(x) = Ae^{i\frac{p}{\hbar}x}$

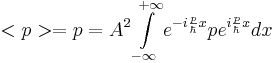
$<p> = p = A^2\int\limits_{-\infty}^{+\infty}e^{-i\frac{p}{\hbar}x}pe^{i\frac{p}{\hbar}x}dx$

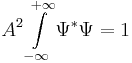
$A^2\int\limits_{-\infty}^{+\infty}\Psi^*\Psi = 1$

Можно ввести следующую форму оператора:

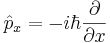
$\hat p_x = -i\hbar\frac{\partial}{\partial x}$

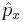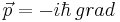Итак, в состоянии с волной де Бройля таким должен быть оператор $\hat p_x$ (проекция на ось х), чтобы выполнялись все постулаыт кв. мех. Далее мы постулируем этот оператор. В трёхмерном случае --- это градиент $\vec p = -i\hbar\,grad$ .

Сформулируем правило задания оператора на основе физической величины. Есть энергия. Как построить оператор, соответствующий этой физической величине?

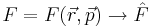
$F=F(\vec r,\vec p)\to \hat F$

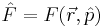
$\hat F = F(\vec r, \hat p)$

Вот так строятся операторы в квантовой механике.

Стоит добавить: в волновой квантовой механике. Есть ещё матричная квантовая механика. Некоторое врем мы будем заниматься волновой квантовой механикой, а потом переёдём к операторной. Волновая механика удобна для описания физических явлений. А вот приложения КМ к ТИ наоборот, волновая мех. не работает, не предст. интереса, а матричная информция работает. И это понятно: матрица --- числа и информация --- числа.

Это дифф. операторы, соотв. физ. величинам, и они работают в волновой КМ.

Допустим, пример: как будет выразаться энергия частицы в классич. физике: 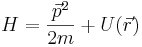$H = \frac{\vec p^2}{2m} + U(\vec r)$ . Действуем по только что описанному правилу: заменяем p на оператор p, а координату оставляем как есть: 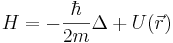$H = -\frac{\hbar}{2m}\Delta + U(\vec r)$ оператор --- градиент, градиент на градиент --- лапласиан. Получили оператор Гамильтона, гамильтониан частицы, которая движется в потенциальном поле.

Запишем св-ва операторов кв. мех.

Операторы квантовой механики линейны. Квантовая механика --- линейная теория. Поэтому, операторы должны быть линейны, и поэтому, кстати, возможен принцип суперпозиции.
Операторы физических величин в кванторвой мезанике являются эрмитовыми операторами. Т.е. выполняется такое условие: 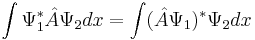$\int\Psi_1^*\hat A\Psi_2 dx = \int(\hat A\Psi_1)^*\Psi_2 dx$ . Следствие: среднее значение ---- действительное, т.е.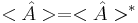 $<\hat A>=<\hat A>^*$
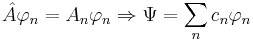
Свойство полноты набора собственных функций: $\hat A\varphi_n=A_n\varphi_n\Rightarrow \Psi=\sum\limits_nc_n\varphi_n$

Одна из важнейших задач КМ: задача на собственные функции и значения операторов.

Если есть оператор A, то задача выглядит след. образом: 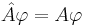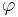$\hat A\varphi = A\varphi$ . $\varphi$ --- собст. функции., A --- собственные числа. Уравнение дифференциальное. Для решения надо добавлять граничные условия. Тогда мы полностью оперделим задачу на собственные значения и собственные функции. Например: оперделить собственные значения и собственные функции для оператора импульса для финитного движения. Определить собственные значения оператора энергии.

Ещё одно свойство: свойство полноты набора собст. функций. Мы решаем задачу и получаем набор собст функции. Этот набор является полным. Полным означает вот что: любая волновая функция может быть разложена в ряд по собст. функциям оператора A.

Ещё одно свойство функций собственных: эти функций образуют не только полный, но и ортонормированный набор.

Тогда что получается: тогда двойная сумма превращается в одинарную:

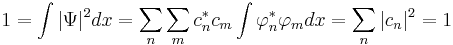
$1 = \int|\Psi|^2dx = \sum\limits_n\sum\limits_mc_n^*c_m\int\varphi_n^*\varphi_mdx = \sum\limits_n|c_n|^2 = 1$

причём зависимость по t исчезла. $| c n | 2$ --- имеет физический смысл вероятности нахождения частицы в этом состоянии.

Вот у нас есть атом воборода. У него есть спектр состояний, есть нижнее состояние, и каждому из сост. соотв. своя волновая функция. $| c n | 2$ --- вероятность того, что электрон находится на n-ном уровне

И можно осущ. переходы в разные представления. И в этом предст. роль волновых функций играет набор $c n$ .

Фактически, мы сделали шаг к переходу к матричной кв. мех.. Именно так мы сделали переход неск. позже.

[править] Уравнение Шредингера

Последний и важнейший вопрос. Играет такое же значение, как и уравнение Ньютона в классической математике.

Шредингер --- известный австрийский физик, который вывел своё уравнение в 1926 году. Выводить мы будем не так. Мы путь его сократим и интуитивно поймём, как он делал это.

Вопрос: нельзя ли развить рег. способ, который для заданной системы давал бы волновую функцию. Эта система может быть очень сложна, например, твёрдое тело, но способ должен быть единым. Такой способ есть, его нашёл Шредингер и способ --- уравнение Шредингера.

Как можно рассуждать:

Это волна. Раз это волна, раз это волновое поле (лектор будет рассм. одном. случай, потом обобщ.), то оно должно подчиняться волновое уравнение. Знаем мы такое уравнение? Знаем, это звук, или ЭМ-уравнение. Какой вид имеет это уравнение? $Ψ(x, t) = A sin(k x + ω t)$ (?)

Это уравнение надо продифференцировать два раза. Получим соотношение между частотой и волновым числом.

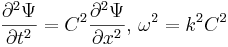
$\frac{\partial^2\Psi}{\partial t^2}=C^2\frac{\partial^2\Psi}{\partial x^2},\,\omega^2=k^2C^2$

Подходит нам это уравнение в случае волновой механики? Нет. Почему? Есть уравнение де Бройля, они проверены экспериментом, значит есть основа. Запишем уравнение де Бройля: $Ψ(x, t) = A e i (k x - ω t)$ (?) Это означает, что слева должнв быть не вторая производная, а первая. Тогда при дифф. получим частоту. Построим такое уравнение:

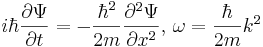
$i\hbar\frac{\partial\Psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial x^2},\,\omega=\frac{\hbar}{2m}k^2$

Мы подобрали коэф. так, чтобы выполн. соотн. В этом смысле всё в порядке. Дальше мы будем обобщать. Что стоит с правой стороны? А это гамильтониан в случае движения по оси х. Значит, то ур., которые мы получили из эвр. сообр, можно записать в общем виде, заменив частную производную вот чем:

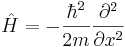
$\hat H = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}$

В таком виде уравнение можно записать.

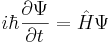
$i\hbar\frac{\partial\Psi}{\partial t}=\hat H\Psi$

А вот теперь сделаем обобщение и в виде постулата введём следующее утверждение: такое уравнение справедливо для любой системы, которая характеризуется гамильтонианом 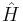$\hat H$ . Оно подтверждается следствиями, и оно было принято физическим миром. Оно было принято сразу после работ Шредингера, поскольку он не только вывел уравн, но и построил модель для атома водорода, и результаты в точности соответствовали результатам Бора, а результаты Бора были проверены экспериментально. Начиная с 1926 года, началось интенсивное применение уравнения Шредингера ко всем ... .

Как бы это уравн. Выглядело бы для атома водорода? Водород: протон и электрон. Будем рассм. движение одного тела, посколько ядро во много раз тяжелее и можно считать его покоящимся. И из этого ур

Последний пункт: стационар. ур. Ш.

Стационарной называется система, гамильтониан которой не зависит от времени. То есть, гамильтониан зависит только от координаты. Тогда $Ψ$ можно факторизовать на чати, зависящие только от координаты и только от времени: 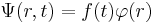$\Psi(r,t)=f(t)\varphi(r)$ . Тогда можно разделить переменные.

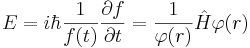
$E=i\hbar\frac{1}{f(t)}\frac{\partial f}{\partial t}=\frac{1}{\varphi(r)}\hat H\varphi(r)$

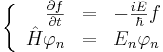
$\left\{ \begin{array}{rcl} \frac{\partial f}{\partial t} & = & -\frac{iE}{\hbar}f \\ \hat H\varphi_n & = & E_n\varphi_n \\ \end{array} \right.$

Второе уравнение и называется стационарным уравнением Шредингера. Оно не зависит от времени. И определяет собственные функции и собственные значения.

Дляч атома водор. ур. выгл. так, и его и решал Ш.

Основы квантовой физики и квантовых вычислений

01 02 03 04 05 06 07 08 09 10 11 12

Календарь

Февраль	13	20	27
Март	05	12	19	26
Апрель	02	09	16	23	30

Эта статья является конспектом лекции.

Эта статья ещё не вычитана. Пожалуйста, вычитайте её и исправьте ошибки, если они есть.

Получено с http://esyr.org/wiki/%D0%9E%D0%9A%D0%A4%D0%B8%D0%9A%D0%92%2C_02_%D0%BB%D0%B5%D0%BA%D1%86%D0%B8%D1%8F_%28%D0%BE%D1%82_20_%D1%84%D0%B5%D0%B2%D1%80%D0%B0%D0%BB%D1%8F%29

Категории: ОКФиКВ | Лекции | Незавершённые статьи

@@ Строка 69: / Строка 69: @@
 Вопросы, которые входят в критерии.
-Первый постулат. Квантовый объект описывается с наибольшей полнотой волн. функцией.
+Первый постулат. Квантовый объект описывается с наибольшей полнотой волновой функцией.
-Второй постулат. Каждой классической физ. вел-не соответствет оператор. Значению физ. величины, измеряемой в эксперименте, соответствует среднее значение оператора этой физической величины.
+Второй постулат. Каждой классической физической величине соответствет оператор. Значению физической величины, измеряемой в эксперименте, соответствует среднее значение оператора этой физической величины.
-Постулат утверждает, что если мы строим теорию квантового объекта, то мы должны отталк. от классич. физ. вел-н. Хотя мы увидим, что это не всегда так, например, спин. Вообще, спин --- объект релятивистской квант. мех., а в нерел. ымы должны отталк. от классич. вел-н.
+Постулат утверждает, что если мы строим теорию квантового объекта, то мы должны отталкиваться от классических физических величин. Хотя мы увидим, что это не всегда так, например, спин. Вообще, спин --- объект релятивистской квантовой механики, а в нерелятивистской мы должны отталкиваться от классических величин.
-Координата. Оператор координаты --- сама координата, умножение. x &lt;x&gt; = интеграл по всей прямой &ksi;*x&ksi;dx
+Координата. Оператор координаты <math>\hat x</math>--- сама координата, умножение на x.
+<math><\hat x> = \int\limits_{-\infty}^{+\infty}\Psi^*x\Psi dx</math>
-&ksi;* --- комплексное сопряжение., интеграл по всей прямой &ksi;*x&ksi;dx = интеграл по всей прямой |&ksi;|^2 x&ksi;dx
+<math>\Psi^*</math> --- комплексное сопряжение., интеграл по всей прямой &ksi;*x&ksi;dx = интеграл по всей прямой |&ksi;|^2 x&ksi;dx
-f(x), &lt;f(x)> = интеграл &ksi;*f(x)&ksi;dx
+f(x), <math><f(x)> = \int\limits_{-\infty}^{+\infty}\Psi^*f(x)\Psi dx</math>
-Оператор импульса. Операторы импульса выглядит так: интеграл по всей прямой &ksi;*p^&ksi;dx
+Оператор импульса. Операторы импульса выглядит так:
-из каких сообр. мы можем получить это: из волны де Бройля. При рассм. волны дБ мы считаем, что импульс задан, и его значение --- среднее значение. &ksi;(x) = Ae<sup>p/&pi; x</sup>
+<math><\hat p> = \int\limits_{-\infty}^{+\infty}\Psi^*\hat p\Psi dx</math>
-Можно ввести следующую форму оператора: ...
+из каких соображений мы можем получить это: из волны де Бройля. При рассмотрении волны де Бройля мы считаем, что импульс задан, и его значение --- среднее значение. <math>\Psi(x) = Ae^{i\frac{p}{\hbar}x}</math>
-Итак, в состоянии с волной де Бройля таким должен быть оператор P (проекция на ось х), чтобы выполнялись все постулаыт кв. мех. Далее мы постулируем этот оператор. В трёхмерном случае --- это градиент ... .
+<math><p> = p = A^2\int\limits_{-\infty}^{+\infty}e^{-i\frac{p}{\hbar}x}pe^{i\frac{p}{\hbar}x}dx</math>
-Сформулируем правило задания оператора на осн. физ. вел-ны. Есть энергия. Как построить оператор, соотв. этой физ. вел-не? ... Вот так строятся импулься в кв. мех.
+<math>A^2\int\limits_{-\infty}^{+\infty}\Psi^*\Psi = 1</math>
-Стоит добавить: в волновой кв. мех. Есть ещё матричная кв. ьех. Некоторое врем мы будем заниматься волновой кв. мех. А потом переёдём к операторной кв. мкех. Волновая механика удобна для описания физических явлений. А вот приложения КМ к ТИ наоборот, волновая мех. не работает, не предст. интереса, а матричная информаия работает. И это понятно: матрица --- числа и информация --- числа.
+Можно ввести следующую форму оператора:
-Это дифф. операторы, соотв. физ. вел-нам, и они работают  в волновой КМ.
+<math>\hat p_x = -i\hbar\frac{\partial}{\partial x}</math>
-Допустим, пример: как будет выразаться энергия частицы в классич. физике: H = '''p'''^2/2m + U('''r'''). Действуем по только что описанному правилу: заменяем p на оператор p, а координату оставляем как есть: H = ... оператор --- градиент, градиент на градиент --- лапласиан. Получили оператор Гамильтона, гамильтониан частицы, которая движется в потенц. поле.
+Итак, в состоянии с волной де Бройля таким должен быть оператор <math>\hat p_x</math> (проекция на ось х), чтобы выполнялись все постулаыт кв. мех. Далее мы постулируем этот оператор. В трёхмерном случае --- это градиент <math>\vec p = -i\hbar\,grad</math> .
+Сформулируем правило задания оператора на основе физической величины. Есть энергия. Как построить оператор, соответствующий этой физической величине?
+<math>F=F(\vec r,\vec p)\to \hat F</math>
+<math>\hat F = F(\vec r, \hat p)</math>
+Вот так строятся операторы в квантовой механике.
+Стоит добавить: в волновой квантовой механике. Есть ещё матричная квантовая механика. Некоторое врем мы будем заниматься волновой квантовой механикой, а потом переёдём к операторной. Волновая механика удобна для описания физических явлений. А вот приложения КМ к ТИ наоборот, волновая мех. не работает, не предст. интереса, а матричная информция работает. И это понятно: матрица --- числа и информация --- числа.
+Это дифф. операторы, соотв. физ. величинам, и они работают в волновой КМ.
+Допустим, пример: как будет выразаться энергия частицы в классич. физике: <math>H = \frac{\vec p^2}{2m} + U(\vec r)</math>. Действуем по только что описанному правилу: заменяем p на оператор p, а координату оставляем как есть: <math>H = -\frac{\hbar}{2m}\Delta + U(\vec r)</math> оператор --- градиент, градиент на градиент --- лапласиан. Получили оператор Гамильтона, гамильтониан частицы, которая движется в потенциальном поле.
 Запишем св-ва операторов кв. мех.
-* Операторы кв. мех. линейны. Квантовая механика --- линейная теория. Поэтому, операторы должны быть линейны, и поэтому, кстати, возможен принцип суперпоз.
+* Операторы квантовой механики линейны. Квантовая механика --- линейная теория. Поэтому, операторы должны быть линейны, и поэтому, кстати, возможен принцип суперпозиции.
-* Операторы физ. величин в кванторвой мезанике являются эрмитовыми операторами. Если выполняется такое условие: интеграл ... . То есть, среднее значение ---- действительное.
+* Операторы физических величин в кванторвой мезанике являются эрмитовыми операторами. Т.е. выполняется такое условие: <math>\int\Psi_1^*\hat A\Psi_2 dx = \int(\hat A\Psi_1)^*\Psi_2 dx</math>. Следствие: среднее значение ---- действительное, т.е. <math><\hat A>=<\hat A>^*</math>
+* Свойство полноты набора собственных функций: <math>\hat A\varphi_n=A_n\varphi_n\Rightarrow \Psi=\sum\limits_nc_n\varphi_n</math>
 Одна из важнейших задач КМ: задача на собственные функции и значения операторов.
-Если есть оператор A, то задача выглядит след. образом: A^&phi; = A&phi;. &phi; --- собст. функции., A&phi; --- собственные числа. Уравнение дифф. Для решения надо добавлять гранич. условия. Тогда мы полностью оперделим задачу на собст. знач. и собст. функции. Например: оперделить собст. знач/функции для  оператора импульса для финитного движения. Определить собст. знач. оператора энергии.
+Если есть оператор A, то задача выглядит след. образом: <math>\hat A\varphi = A\varphi</math>. <math>\varphi</math> --- собст. функции., A --- собственные числа. Уравнение дифференциальное. Для решения надо добавлять граничные условия. Тогда мы полностью оперделим задачу на собственные значения и собственные функции. Например: оперделить собственные значения и собственные функции для оператора импульса для финитного движения. Определить собственные значения оператора энергии.
 Ещё одно свойство: свойство полноты набора собст. функций. Мы решаем задачу и получаем набор собст функции. Этот набор является полным. Полным означает вот что: любая волновая функция может быть разложена в ряд по собст. функциям оператора A.
@@ Строка 110: / Строка 126: @@
 Ещё одно свойство функций собственных: эти функций образуют не только полный, но и ортонормированный набор.
-Тогда что получается: тогда двойная сумма превращается в одинарную, 1 = сумма по n |C_N(t)|^2, причём  зависимость по t исчезла. |C_N|^2 --- имеет физ. смысл как вероятность нахождения частицы в этом состоянии.
+Тогда что получается: тогда двойная сумма превращается в одинарную:
-Вот у нас есть атом воборода. У него есть спектр состояний, есть нижнее состояние, и каждому из сост. соотв. своя волновая функция. |C_N|^2 --- вероятность того, что электрон находится нга n-ном уровне
+<math>1 = \int|\Psi|^2dx = \sum\limits_n\sum\limits_mc_n^*c_m\int\varphi_n^*\varphi_mdx = \sum\limits_n|c_n|^2 = 1</math>
-И можно осущ. переходы в разные представления. И в этом предст. роль волновых функций играет набор c_n.
+причём  зависимость по t исчезла. <math>|c_n|^2</math> --- имеет физический смысл вероятности нахождения частицы в этом состоянии.
+Вот у нас есть атом воборода. У него есть спектр состояний, есть нижнее состояние, и каждому из сост. соотв. своя волновая функция. <math>|c_n|^2</math> --- вероятность того, что электрон находится на n-ном уровне
+И можно осущ. переходы в разные представления. И в этом предст. роль волновых функций играет набор <math>c_n</math>.
 Фактически, мы сделали шаг к переходу к матричной кв. мех.. Именно так мы сделали переход неск. позже.
@@ Строка 120: / Строка 140: @@
 == Уравнение Шредингера ==
-Последний и важнейший вопрос. Играет такое же значение, как и уравнение Ньютона в классич. математике.
+Последний и важнейший вопрос. Играет такое же значение, как и уравнение Ньютона в классической математике.
-Ш. --- известный австрийский физик, который вывел своё уравнение в 1926(?) году. выводить мы будем не так. Мы путь его сократим и инттуитивно поймём, как он делал это.
+Шредингер --- известный австрийский физик, который вывел своё уравнение в 1926 <!-- согласно английской википедии, в русской 1925 написано --> году. Выводить мы будем не так. Мы путь его сократим и интуитивно поймём, как он делал это.
-Вопрос: нельзя ли развить рег. способ, который для заданной системы давал бы волновую функцию. Эта система может быть очень сложна, например, твёрдое тело, но способ должен быть единым. Такой способ есть, его нашёл Ш. и способ --- уравнение Ш.
+Вопрос: нельзя ли развить рег. способ, который для заданной системы давал бы волновую функцию. Эта система может быть очень сложна, например, твёрдое тело, но способ должен быть единым. Такой способ есть, его нашёл Шредингер и способ --- уравнение Шредингера.
 Как можно рассуждать:
-* Это волна. Раз это волна, раз это волновое поле (лектор будет рассм. одном. случай, потом обобщ.), то оно должно подчиняться волн. ур. Знаем мы такое ур.? Знаем, это звук, или ЭМ-уравнение. Какой вид имеет это уравнение? ...
+* Это волна. Раз это волна, раз это волновое поле (лектор будет рассм. одном. случай, потом обобщ.), то оно должно подчиняться волновое уравнение. Знаем мы такое уравнение? Знаем, это звук, или ЭМ-уравнение. Какой вид имеет это уравнение? <math>\Psi(x,t)=A\sin(kx+\omega t)</math>(?)
-Это уравн. надо продифф. два раза. Получим соот. между частотой и волн. числом. Подходит нам это уравнение в случае волн. мезаники? Нет. Почему? Есть ур. де Бройля, они проверены эксперим., значит есть основа. Запишем ур. деБройля: ... Это озн., что слева должнв быть не вторая производная, а первая. Тогда при дифф. получим частоту. Построим такое уравнение: ... . Мы подобрали коэф. так, чтобдывыполн. соотн. В этом смысле всё в порядке. ДАльше мы будем обобщать. Что стоит с правой стороны? А это гамильтониан в случае движения по оси х. Значит, то ур., которые мы получили из эвр.  сообр, можно записать в общем виде, заменив частную производную вот чем: ... . В таком виде уравнение можно записать. А вот теперь сделаем обобщение и в виде постулата введём след. утверждение: такое уравн. справедливо для любой системыЮ которая харак. гамильтонианом H. Оно подтверждается следствиями, и оно было принято физич. миром. Оно было принято сразу после работ Ш., поскольку он не только вывел уравн, но и построил модель для атома водорода, и результаты в точности соотв. результатам Бора, а результаты Бора были проверены эксперим.. Начиная с 1926 года, началось интенс. применение ур. Ш. ко всем ... .
+Это уравнение надо продифференцировать два раза. Получим соотношение между частотой и волновым числом.
+<math>\frac{\partial^2\Psi}{\partial t^2}=C^2\frac{\partial^2\Psi}{\partial x^2},\,\omega^2=k^2C^2</math>
+Подходит нам это уравнение в случае волновой механики? Нет. Почему? Есть уравнение де Бройля, они проверены экспериментом, значит есть основа. Запишем уравнение де Бройля: <math>\Psi(x,t)=Ae^{i(kx-\omega t)}</math>(?) Это означает, что слева должнв быть не вторая производная, а первая. Тогда при дифф. получим частоту. Построим такое уравнение:
+<math>i\hbar\frac{\partial\Psi}{\partial t}=-\frac{\hbar^2}{2m}\frac{\partial^2\Psi}{\partial x^2},\,\omega=\frac{\hbar}{2m}k^2</math>
+Мы подобрали коэф. так, чтобы выполн. соотн. В этом смысле всё в порядке. Дальше мы будем обобщать. Что стоит с правой стороны? А это гамильтониан в случае движения по оси х. Значит, то ур., которые мы получили из эвр.  сообр, можно записать в общем виде, заменив частную производную вот чем:
+<math>\hat H = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}</math>
+В таком виде уравнение можно записать.
+<math>i\hbar\frac{\partial\Psi}{\partial t}=\hat H\Psi</math>
+А вот теперь сделаем обобщение и в виде постулата введём следующее утверждение: такое уравнение справедливо для любой системы, которая характеризуется гамильтонианом <math>\hat H</math>. Оно подтверждается следствиями, и оно было принято физическим миром. Оно было принято сразу после работ Шредингера, поскольку он не только вывел уравн, но и построил модель для атома водорода, и результаты в точности соответствовали результатам Бора, а результаты Бора были проверены экспериментально. Начиная с 1926 года, началось интенсивное применение уравнения Шредингера ко всем ... .
 Как бы это уравн. Выглядело бы для атома водорода? Водород: протон и электрон. Будем рассм. движение одного тела, посколько ядро во много раз тяжелее и можно считать его покоящимся. И из этого ур
@@ Строка 134: / Строка 170: @@
 Последний пункт: стационар. ур. Ш.
-Стационарной называется системА, гамильтониан которой не зависит от времени. То есть, гамильт. зависит только от координаты. Тогда его можно факторизовать на чати, зависящ. только от коорд. и только от времени. Тогда можно разделить переменные.
+Стационарной называется система, гамильтониан которой не зависит от времени. То есть, гамильтониан зависит только от координаты. Тогда <math>\Psi</math> можно факторизовать на чати, зависящие только от координаты и только от времени: <math>\Psi(r,t)=f(t)\varphi(r)</math>. Тогда можно разделить переменные.
+<math>E=i\hbar\frac{1}{f(t)}\frac{\partial f}{\partial t}=\frac{1}{\varphi(r)}\hat H\varphi(r)</math>
+<math>\left\{
+\begin{array}{rcl}
+\frac{\partial f}{\partial t} & = & -\frac{iE}{\hbar}f \\
+\hat H\varphi_n & = & E_n\varphi_n \\
+\end{array}
+\right.</math>
-Второе уравнение и наз. с. у. Ш. Оно не зависит от времени. И определяет собственные функции и собст. значения.
+Второе уравнение и называется стационарным уравнением Шредингера. Оно не зависит от времени. И определяет собственные функции и собственные значения.
 Дляч атома водор. ур. выгл. так, и его и решал Ш.

ОКФиКВ, 02 лекция (от 20 февраля)

Материал из eSyr's wiki.

Текущая версия

[править] Операторы квантовой механики

[править] Уравнение Шредингера

Просмотры

Личные инструменты

Навигация

инструменты

Разделы

Спецкурсы

9 семестр

7 семестр

5 семестр

3 семестр

Поиск

Инструменты