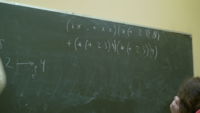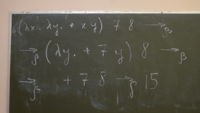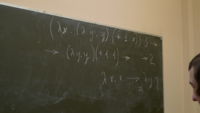Парадигмы программирования, 06 лекция (от 29 октября)
Материал из eSyr's wiki.
(Новая: "На эту тему мне понравилась татуировка с Y-combinator" лямбда-исчисления. На самом деле, л-исчисл. имеют не ...) |
|||
| Строка 1: | Строка 1: | ||
| - | + | [[Image:paradigm_091029_01.jpg|thumb|right|300px|«На эту тему мне понравилась [http://theartoftattoo.files.wordpress.com/2009/04/y-combinator.jpg татуировка с Y-combinator»]]] | |
| - | лямбда-исчисления | + | = лямбда-исчисления = |
На самом деле, л-исчисл. имеют не совсем прямое. л-исчисл. было придумано Чёрчем задолго до программирования. | На самом деле, л-исчисл. имеют не совсем прямое. л-исчисл. было придумано Чёрчем задолго до программирования. | ||
| Строка 13: | Строка 13: | ||
Как в л-исчисл запис. функция: | Как в л-исчисл запис. функция: | ||
| - | lambda x . и дальше выражение, задающее функцию. Как оно задётся, бывают разные способы. Обычно исп. польскую нотацию | + | λ x . и дальше выражение, задающее функцию. Как оно задётся, бывают разные способы. Обычно исп. польскую нотацию |
| - | lambda x . * 3 x | + | λ x . * 3 x |
как это прочитать: | как это прочитать: | ||
| - | * lambda — "функция от" | + | * λ — "функция от" |
* . — которая возвращает | * . — которая возвращает | ||
Большинство авторов рассм. ф-цию от одного параметра, но мощности это не уменьшает. Да, некоторые авторы пишут | Большинство авторов рассм. ф-цию от одного параметра, но мощности это не уменьшает. Да, некоторые авторы пишут | ||
| - | lambda x y z . + x * y z | + | λ x y z . + x * y z |
Но большинство всё же пишут | Но большинство всё же пишут | ||
| - | lambda x . lambda y . lambda z . + x * y z | + | λ x . λ y . λ z . + x * y z |
Такая конструкция наз. лямбда-абстр, то, что после точки — телом. Как видно, в теле может содержаться произв. л-выр., в том числе лямбда. | Такая конструкция наз. лямбда-абстр, то, что после точки — телом. Как видно, в теле может содержаться произв. л-выр., в том числе лямбда. | ||
| Строка 35: | Строка 35: | ||
Чисто синтаксически, функцию всегда применяют к самому левому арг., то есть, если есть такая запись: | Чисто синтаксически, функцию всегда применяют к самому левому арг., то есть, если есть такая запись: | ||
| - | (...((lambda x_1 . lambda x_2 . ... lambda x_n . E) a_1) a_2) ...) a_n | + | (...((λ x_1 . λ x_2 . ... λ x_n . E) a_1) a_2) ...) a_n |
То есть соглащ., что такое выр. можно записать неск. короче: | То есть соглащ., что такое выр. можно записать неск. короче: | ||
| - | (lambda x_1 . lamda x_2 . ... lambda x_n . E) a_1 a_2 ... a_n | + | (λ x_1 . lamda x_2 . ... λ x_n . E) a_1 a_2 ... a_n |
Более формально можно записать в виде БНФ: | Более формально можно записать в виде БНФ: | ||
| - | <exp> ::= lambda <id> . <exp> | <id> | <exp> <exp> | (<exp>) | <const> | + | <exp> ::= λ <id> . <exp> | <id> | <exp> <exp> | (<exp>) | <const> |
<id> ::= идентификатор (какие могут быть идент --- зависит от того, какой стиль приняли) | <id> ::= идентификатор (какие могут быть идент --- зависит от того, какой стиль приняли) | ||
<const> ::= константы | <const> ::= константы | ||
| Строка 66: | Строка 66: | ||
42 | 42 | ||
(+ 6) ; функция, которая прибавляет 6 | (+ 6) ; функция, которая прибавляет 6 | ||
| - | lambda y . * 2 y ; лямбда-абстракция | + | λ y . * 2 y ; лямбда-абстракция |
В многоточие жироне входит в том числе cond. Он аналогичн лисповскому if. Похоже на сишную тернарную операцию. | В многоточие жироне входит в том числе cond. Он аналогичн лисповскому if. Похоже на сишную тернарную операцию. | ||
| - | (lambda f . lmbda a lambda b . f a b) (lambda x . (lambda y . x)) | + | (λ f . lmbda a λ b . f a b) (λ x . (λ y . x)) |
| - | Вернёт a ((lambda x . (lambda y . x)) как ф-ция от двух. арг подст. в f, и сама по себе возвр. первый арг.). | + | Вернёт a ((λ x . (λ y . x)) как ф-ция от двух. арг подст. в f, и сама по себе возвр. первый арг.). |
| - | lambda f . lambda x . COND (= x 1) x (* x (f (- x 1))) | + | λ f . λ x . COND (= x 1) x (* x (f (- x 1))) |
Имеет отн. к вычислению факториала. Вообще, без имён функций тяжело, дальше мы посмотрим, как это решить. | Имеет отн. к вычислению факториала. Вообще, без имён функций тяжело, дальше мы посмотрим, как это решить. | ||
| Строка 80: | Строка 80: | ||
Как л-выр. вычисл. Т. н. правила редукции. | Как л-выр. вычисл. Т. н. правила редукции. | ||
* Константы редуц. в себя | * Константы редуц. в себя | ||
| - | * Функция и арг. Применяется дельта-правило. Например: + 1 2 | + | * Функция и арг. Применяется дельта-правило. Например: + 1 2 →<sub>δ</sub> 3. Из этого выр. по дельта-правилу, или, применив дельта-редукцию, получаем 3. Понятно, что дельта-правила есть для каждой функции. Например, у нас есть выр. |
| - | * (+ 1 2) (- 4 1) | + | * (+ 1 2) (- 4 1) →<sub>δ</sub> * (+ 1 2) 3 →<sub>δ</sub> * 3 3 →<sub>δ</sub> 9 |
* Применение ф-ции, напис. через лямбда-абстракцию. Заменяем чисто текстуально, результат замены --- рез-т выражения: | * Применение ф-ции, напис. через лямбда-абстракцию. Заменяем чисто текстуально, результат замены --- рез-т выражения: | ||
| - | (lambda x . * x x) 2 | + | (λ x . * x x) 2 →<sub>β</sub> * 2 2 →<sub>δ</sub> 4 |
| - | (lambda x . + x x) (* (+ 2 3) 4) | + | (λ x . + x x) (* (+ 2 3) 4) →<sub>β</sub> + (* (+ 2 3) 4) (* (+ 2 3) 4) |
: Текстуально оно становится длиннее, но мы избавляемся от символа лямбда. | : Текстуально оно становится длиннее, но мы избавляемся от символа лямбда. | ||
| - | (lambda x . lambda y . + x y) 7 8 | + | (λ x . λ y . + x y) 7 8 →<sub>β</sub> (λ y . + 7 y) 8 →<sub>β</sub> + 7 8 →<sub>δ</sub> 15 |
Редуцируемая часть. выр наз. редексом (redex, reducible expression) | Редуцируемая часть. выр наз. редексом (redex, reducible expression) | ||
| Строка 94: | Строка 94: | ||
Имеется некий подводный камень, связанный с одноим. символами. Рассмотрим выражение: | Имеется некий подводный камень, связанный с одноим. символами. Рассмотрим выражение: | ||
| - | lambda x . (lambda x . x) (+ 1 x) | + | λ x . (λ x . x) (+ 1 x) |
В чём здесь неприятность? Очевидно, что | В чём здесь неприятность? Очевидно, что | ||
| - | lambda x_2 . (lambda lambda x_1 . x_1) (+ 1 x_1) | + | λ x_2 . (λ λ x_1 . x_1) (+ 1 x_1) |
Если взять это в скобки и где-то применить, то понятно, что получится не то, что хотели. Получается конфликт имён. Как это разрешить? Например, постановить, что если мы подобные вещи применяем к чему-то, то внутри ничего не трогать. | Если взять это в скобки и где-то применить, то понятно, что получится не то, что хотели. Получается конфликт имён. Как это разрешить? Например, постановить, что если мы подобные вещи применяем к чему-то, то внутри ничего не трогать. | ||
| Строка 106: | Строка 106: | ||
Если не учитывать контекст имён, то что получится: | Если не учитывать контекст имён, то что получится: | ||
| - | (lambda x . (lambda x . x) (+ 1 x)) 3 -> (lambda x . 3) (+ 1 3) -> 7 | + | (λ x . (λ x . x) (+ 1 x)) 3 -> (λ x . 3) (+ 1 3) -> 7 |
| - | (lambda x . (lambda y . y) (+ 1 x)) 3 -> (lambda y . y) (+ 1 3) -> ... -> 8 | + | (λ x . (λ y . y) (+ 1 x)) 3 -> (λ y . y) (+ 1 3) -> ... -> 8 |
То есть вот, конфликты имён бывают, конфликты имён ращреш. альфа-преобр, это не совсем ред., хотя записывается также: | То есть вот, конфликты имён бывают, конфликты имён ращреш. альфа-преобр, это не совсем ред., хотя записывается также: | ||
| - | lambda x. x | + | λ x. x →<sub>α</sub> λ y . y |
Порядок выбор редексов для редукции. В л-выр может быть неск. редексов, и вопрос, с какого начать? Вопрос интересный и весьма принципиальный. Рассмотрим пример: | Порядок выбор редексов для редукции. В л-выр может быть неск. редексов, и вопрос, с какого начать? Вопрос интересный и весьма принципиальный. Рассмотрим пример: | ||
| - | (lambda f . lambda x . f 4 x) (lambda y . lambda x . + x y) 3 -> | + | (λ f . λ x . f 4 x) (λ y . λ x . + x y) 3 -> |
-------- --------------------------- | -------- --------------------------- | ||
---------------------------------------------------------- | ---------------------------------------------------------- | ||
| - | (lambda x . (lambda y . lambda x + x y) 4 x) 3 -> | + | (λ x . (λ y . λ x + x y) 4 x) 3 -> |
---- ---- | ---- ---- | ||
на самом деле, тут в обоих случаях получится одно и то же | на самом деле, тут в обоих случаях получится одно и то же | ||
| - | 1. (lambda y . lambda x + x y) 4 3 -> (lambda x . + x 4) 3 -> + 3 4 -> 7 | + | 1. (λ y . λ x + x y) 4 3 -> (λ x . + x 4) 3 -> + 3 4 -> 7 |
| - | 2. (lambda x . (lambda x . + x 4) x) 3 -> (lambda x . + x 4) 3 -> + 3 4 -> 7 | + | 2. (λ x . (λ x . + x 4) x) 3 -> (λ x . + x 4) 3 -> + 3 4 -> 7 |
В принципе, до какой-то степени так и должно быть, но есть теорема Чёрча-Россера, которая гласит, что если у лямбда-выр. есть норм. форма, то она только одна (если неск., то они эквив. с точностью до алф. преобр.). Из этого следует, что она аже достигается. Но выбрав нехороший порядок редукции, то можно не прийти к норм. форме вообще. Есть классич. пример, когда один порядок не приводит к норм. форме вооббще никогда, другой же за один шаг. | В принципе, до какой-то степени так и должно быть, но есть теорема Чёрча-Россера, которая гласит, что если у лямбда-выр. есть норм. форма, то она только одна (если неск., то они эквив. с точностью до алф. преобр.). Из этого следует, что она аже достигается. Но выбрав нехороший порядок редукции, то можно не прийти к норм. форме вообще. Есть классич. пример, когда один порядок не приводит к норм. форме вооббще никогда, другой же за один шаг. | ||
| - | (lambda x . lambda y . y) ((lambda z . z z) (lambda z . z. z)) | + | (λ x . λ y . y) ((λ z . z z) (λ z . z. z)) |
Здесь есть два варианта: | Здесь есть два варианта: | ||
| - | (lambda x . lambda y . y) ((lambda z . z z) (lambda z . z. z)) | + | (λ x . λ y . y) ((λ z . z z) (λ z . z. z)) |
- ------------------------------------ | - ------------------------------------ | ||
тогда мы достигаем результат за один шаг: | тогда мы достигаем результат за один шаг: | ||
| - | lambda y . y | + | λ y . y |
но есть и второй редекс: | но есть и второй редекс: | ||
| - | (lambda x . lambda y . y) ((lambda z . z z) (lambda z . z. z)) | + | (λ x . λ y . y) ((λ z . z z) (λ z . z. z)) |
---------------------------------- | ---------------------------------- | ||
но он при применении даст сам себя: | но он при применении даст сам себя: | ||
| - | (lambda x . lambda y . y) ((lambda z . z z) (lambda z . z. z)) | + | (λ x . λ y . y) ((λ z . z z) (λ z . z. z)) |
Вопрос, какой же редекс тогда надо выбирать и зачем? Введём неск. определений. | Вопрос, какой же редекс тогда надо выбирать и зачем? Введём неск. определений. | ||
| Строка 165: | Строка 165: | ||
Введём такую вещб, как понятие связанных и свободных переменных | Введём такую вещб, как понятие связанных и свободных переменных | ||
| - | lambda x . x y | + | λ x . x y |
Понятно, что x связ., а y --- вободная. Если чуть строже, то построим мн-во FV(E) (free variables(expression)). Как оно вводится: | Понятно, что x связ., а y --- вободная. Если чуть строже, то построим мн-во FV(E) (free variables(expression)). Как оно вводится: | ||
| Строка 171: | Строка 171: | ||
* FV(c) = ∅ | * FV(c) = ∅ | ||
* FV(E_1, E_2) = FV(E_1) ∪ FV(e_2) | * FV(E_1, E_2) = FV(E_1) ∪ FV(e_2) | ||
| - | * FV(lambda x . E_1) = FV(E_1) \ {x} | + | * FV(λ x . E_1) = FV(E_1) \ {x} |
Аналогично можно ввести мн-во Bound variables, BV(E): | Аналогично можно ввести мн-во Bound variables, BV(E): | ||
| Строка 177: | Строка 177: | ||
* BV(c) = ∅ | * BV(c) = ∅ | ||
* BV(E_1, E_2) = BV(E_1) ∪ BV(e_2) ; отсюда следует, что прееменная может быт ьи свободная, и связана, но свободна в одной части, а связана в другой | * BV(E_1, E_2) = BV(E_1) ∪ BV(e_2) ; отсюда следует, что прееменная может быт ьи свободная, и связана, но свободна в одной части, а связана в другой | ||
| - | * BV(lambda x . E_1) = BV(E_1) ∪ {x} | + | * BV(λ x . E_1) = BV(E_1) ∪ {x} |
Выражение, в котором нет связ. переменных, наз. замкнутым. Замкнутыми выр. ещё наз. комбинаторами. | Выражение, в котором нет связ. переменных, наз. замкнутым. Замкнутыми выр. ещё наз. комбинаторами. | ||
| - | Если x ∉ FV(E), то можно вести речь об & | + | Если x ∉ FV(E), то можно вести речь об η-преобразовании. |
| - | Можно заметить, что lambda x . E x есть то же самое, что E. Попробуем и то, и другое к a: | + | Можно заметить, что λ x . E x есть то же самое, что E. Попробуем и то, и другое к a: |
E a | E a | ||
| - | (lambda x . E x) a | + | (λ x . E x) a →<sub>β</sub> E a |
Главное, чтобы в E не было свободной переменной x, иначе ничего не выйдет. Соотв, делаем это преобр.: | Главное, чтобы в E не было свободной переменной x, иначе ничего не выйдет. Соотв, делаем это преобр.: | ||
| - | E | + | E →<sub>η</sub> λ x. E x |
| - | Что оно позв. делать? Например, част. применение встроенных функций. Например, если есть * x y. Является ли * 3 л-выр? Да. А как же с ним работать. Применим & | + | Что оно позв. делать? Например, част. применение встроенных функций. Например, если есть * x y. Является ли * 3 л-выр? Да. А как же с ним работать. Применим η-преобр, получим λ x . * 3 x. Благодаря этому мы можем делать частичное применение функций. |
... это называется карринг, по имени учёного Карри (Curry). | ... это называется карринг, по имени учёного Карри (Curry). | ||
| Строка 201: | Строка 201: | ||
Лектор напишет её сначала на лиспе: | Лектор напишет её сначала на лиспе: | ||
| - | (setq f #'(lambda (s x) (if (= x 0) 0 (+ x (funcall s s (- x 1)))))) | + | (setq f #'(λ (s x) (if (= x 0) 0 (+ x (funcall s s (- x 1)))))) |
Что теперь сделать? Нао её вызвать, подав ей на вход число и её саму. Как это сделать? | Что теперь сделать? Нао её вызвать, подав ей на вход число и её саму. Как это сделать? | ||
| Строка 209: | Строка 209: | ||
можно то же самое сделать и на лямбда-абстракциях | можно то же самое сделать и на лямбда-абстракциях | ||
| - | lambda s . lambda x . COND (= x 0) 0 (+ x (s (- x 1))) | + | λ s . λ x . COND (= x 0) 0 (+ x (s (- x 1))) |
Сущ. неподв. точка, т. е. f(x) = x, и она есть для кажого лямбда-выр. | Сущ. неподв. точка, т. е. f(x) = x, и она есть для кажого лямбда-выр. | ||
| Строка 219: | Строка 219: | ||
Как выглядит Y-combinator: | Как выглядит Y-combinator: | ||
| - | Y = lambda h . (lambda x . h (x x)) (lambda x . h (x x)) | + | Y = λ h . (λ x . h (x x)) (λ x . h (x x)) |
теперь осталось что? | теперь осталось что? | ||
| - | Y lambda s . lambda x . COND (= x 0) 0 (+ x (s (- x 1))) | + | Y λ s . λ x . COND (= x 0) 0 (+ x (s (- x 1))) |
И отредуцировать. Результатом будет функция, от одного арг., выч. сумму. | И отредуцировать. Результатом будет функция, от одного арг., выч. сумму. | ||
y-comb. используется в haskell. | y-comb. используется в haskell. | ||
| + | |||
| + | <gallery perrow="5" widths="200"> | ||
| + | Изображение:Paradigm 091029 02.jpg|λ-исчисление. | ||
| + | Изображение:Paradigm 091029 03.jpg|Сокращённая форма для нескольких функций. | ||
| + | Изображение:Paradigm 091029 04.jpg|БНФ для λ-выражений. | ||
| + | Изображение:Paradigm 091029 05.jpg|БНФ для λ-выражений. | ||
| + | Изображение:Paradigm 091029 06.jpg|β-редукция, δ-редукция. | ||
| + | Изображение:Paradigm 091029 07.jpg|Пример с увеличением текстуальной длины выражения при применении β-редукции. | ||
| + | Изображение:Paradigm 091029 08.jpg|Пример с увеличением текстуальной длины выражения при применении β-редукции. Исправленный вариант. | ||
| + | Изображение:Paradigm 091029 09.jpg|Пример на использование β-редукции. | ||
| + | Изображение:Paradigm 091029 10.jpg|Конфликт имён. | ||
| + | Изображение:Paradigm 091029 11.jpg|α-преобразование. | ||
| + | Изображение:Paradigm 091029 12.jpg|Разный порядок выбора редексов для редукции. | ||
| + | Изображение:Paradigm 091029 13.jpg|Пример с бесконечной ветвью редуцирования редексов. | ||
| + | Изображение:Paradigm 091029 14.jpg|Почему ленивое вычисление логических выражение не есть ленивые вычисления. | ||
| + | Изображение:Paradigm 091029 15.jpg|Построение множеств free variables и bounded variables. | ||
| + | Изображение:Paradigm 091029 16.jpg|η-преобразование. | ||
| + | Изображение:Paradigm 091029 17.jpg|η-преобразование. | ||
| + | Изображение:Paradigm 091029 18.jpg|Пример использования η-преобразования. | ||
| + | Изображение:Paradigm 091029 19.jpg|Currying | ||
| + | <gallery> | ||
{{Парадигмы программирования}} | {{Парадигмы программирования}} | ||
{{Lection-stub}} | {{Lection-stub}} | ||
Версия 09:17, 30 октября 2009

лямбда-исчисления
На самом деле, л-исчисл. имеют не совсем прямое. л-исчисл. было придумано Чёрчем задолго до программирования.
Похоже на то, что любую функцию, которая за конечное время даёт рез-т от конечного числа аргументов, записать можно. Также для неё можно сделать МТ, и т. д.
Л-вычисл это мат. абстр., некий формализм, прямого отн. к прогр. не имеющ.
Есть легенда, что еогда МакКарти писал лисп, он вдохновился л-исчисл, и лисп писался как реализ. л-исчисл. Это не так, хотя впоследствии лямбда туда была добавлена.
Как в л-исчисл запис. функция:
λ x . и дальше выражение, задающее функцию. Как оно задётся, бывают разные способы. Обычно исп. польскую нотацию
λ x . * 3 x
как это прочитать:
- λ — "функция от"
- . — которая возвращает
Большинство авторов рассм. ф-цию от одного параметра, но мощности это не уменьшает. Да, некоторые авторы пишут
λ x y z . + x * y z
Но большинство всё же пишут
λ x . λ y . λ z . + x * y z
Такая конструкция наз. лямбда-абстр, то, что после точки — телом. Как видно, в теле может содержаться произв. л-выр., в том числе лямбда.
Если мы видем два лямбда-выр., E_1 E_2, то это обычно значит, что первое выр. — функция, а второе, знач, к котторому его нужно применить.
Чисто синтаксически, функцию всегда применяют к самому левому арг., то есть, если есть такая запись:
(...((λ x_1 . λ x_2 . ... λ x_n . E) a_1) a_2) ...) a_n
То есть соглащ., что такое выр. можно записать неск. короче:
(λ x_1 . lamda x_2 . ... λ x_n . E) a_1 a_2 ... a_n
Более формально можно записать в виде БНФ:
<exp> ::= λ <id> . <exp> | <id> | <exp> <exp> | (<exp>) | <const> <id> ::= идентификатор (какие могут быть идент --- зависит от того, какой стиль приняли) <const> ::= константы
Константы заслуживают более внимательного рассмотрения. Конст. могут обозначать:
- Числа. Числа могут быть как целые, так и веществ. В больш. случае, когда рассм. л-выч., обычно до вещ. чисел не доходят.
- Булевы значения: Истина и Ложь. Как конкр. их обозначить, это тоже вопрос философский.
- [ Строки ]. Далеко не все авторы про них вспоминают
- Пустой список. Обычно его обозн. <>, хотя можно обозн. как угодно.
- Функции
- * . + - ....
- Знаки отношений: < > = != >= ...
- Функции работы со списками: CONS, HEAD, TAIL, NULL (предикат, проверка на пустой список)
- Иногда некоторые авторы, в частн., Филд, Харрисон, считают необх. ввод кортежей. TUPLE-n, INDEX
- COND
- ...
Вообще, можно делать лямбда-выч. без констант, сконстр. из из первич. понятий, но это к прогр. мало отношения имеет. Без них тяжело. Сначала вводятся списки, потом числа как списки разной длины, а чтобы ввести умножение, нужно неск. страниц исписать.
Примеры лямбда-выражений. Самое простое — просто константа.
42 (+ 6) ; функция, которая прибавляет 6 λ y . * 2 y ; лямбда-абстракция
В многоточие жироне входит в том числе cond. Он аналогичн лисповскому if. Похоже на сишную тернарную операцию.
(λ f . lmbda a λ b . f a b) (λ x . (λ y . x))
Вернёт a ((λ x . (λ y . x)) как ф-ция от двух. арг подст. в f, и сама по себе возвр. первый арг.).
λ f . λ x . COND (= x 1) x (* x (f (- x 1)))
Имеет отн. к вычислению факториала. Вообще, без имён функций тяжело, дальше мы посмотрим, как это решить.
Как л-выр. вычисл. Т. н. правила редукции.
- Константы редуц. в себя
- Функция и арг. Применяется дельта-правило. Например: + 1 2 →δ 3. Из этого выр. по дельта-правилу, или, применив дельта-редукцию, получаем 3. Понятно, что дельта-правила есть для каждой функции. Например, у нас есть выр.
* (+ 1 2) (- 4 1) →δ * (+ 1 2) 3 →δ * 3 3 →δ 9
- Применение ф-ции, напис. через лямбда-абстракцию. Заменяем чисто текстуально, результат замены --- рез-т выражения:
(λ x . * x x) 2 →β * 2 2 →δ 4 (λ x . + x x) (* (+ 2 3) 4) →β + (* (+ 2 3) 4) (* (+ 2 3) 4)
- Текстуально оно становится длиннее, но мы избавляемся от символа лямбда.
(λ x . λ y . + x y) 7 8 →β (λ y . + 7 y) 8 →β + 7 8 →δ 15
Редуцируемая часть. выр наз. редексом (redex, reducible expression)
Если редаксов в выр. нет, тогда говорят, что выр. имеет норм. форму.
Имеется некий подводный камень, связанный с одноим. символами. Рассмотрим выражение:
λ x . (λ x . x) (+ 1 x)
В чём здесь неприятность? Очевидно, что
λ x_2 . (λ λ x_1 . x_1) (+ 1 x_1)
Если взять это в скобки и где-то применить, то понятно, что получится не то, что хотели. Получается конфликт имён. Как это разрешить? Например, постановить, что если мы подобные вещи применяем к чему-то, то внутри ничего не трогать.
Есть второй вариант, т. н. альфа-преобразовнаие. Оно не наз. редукцие, поск. оно ничего не упрощ., оно переименовывает пременную.
Если не учитывать контекст имён, то что получится:
(λ x . (λ x . x) (+ 1 x)) 3 -> (λ x . 3) (+ 1 3) -> 7 (λ x . (λ y . y) (+ 1 x)) 3 -> (λ y . y) (+ 1 3) -> ... -> 8
То есть вот, конфликты имён бывают, конфликты имён ращреш. альфа-преобр, это не совсем ред., хотя записывается также:
λ x. x →α λ y . y
Порядок выбор редексов для редукции. В л-выр может быть неск. редексов, и вопрос, с какого начать? Вопрос интересный и весьма принципиальный. Рассмотрим пример:
(λ f . λ x . f 4 x) (λ y . λ x . + x y) 3 ->
-------- ---------------------------
----------------------------------------------------------
(λ x . (λ y . λ x + x y) 4 x) 3 ->
---- ----
на самом деле, тут в обоих случаях получится одно и то же
1. (λ y . λ x + x y) 4 3 -> (λ x . + x 4) 3 -> + 3 4 -> 7 2. (λ x . (λ x . + x 4) x) 3 -> (λ x . + x 4) 3 -> + 3 4 -> 7
В принципе, до какой-то степени так и должно быть, но есть теорема Чёрча-Россера, которая гласит, что если у лямбда-выр. есть норм. форма, то она только одна (если неск., то они эквив. с точностью до алф. преобр.). Из этого следует, что она аже достигается. Но выбрав нехороший порядок редукции, то можно не прийти к норм. форме вообще. Есть классич. пример, когда один порядок не приводит к норм. форме вооббще никогда, другой же за один шаг.
(λ x . λ y . y) ((λ z . z z) (λ z . z. z))
Здесь есть два варианта:
(λ x . λ y . y) ((λ z . z z) (λ z . z. z))
- ------------------------------------
тогда мы достигаем результат за один шаг:
λ y . y
но есть и второй редекс:
(λ x . λ y . y) ((λ z . z z) (λ z . z. z))
----------------------------------
но он при применении даст сам себя:
(λ x . λ y . y) ((λ z . z z) (λ z . z. z))
Вопрос, какой же редекс тогда надо выбирать и зачем? Введём неск. определений.
* Самый левый редекс --- его лямбда или имя примитивной функции находятся текстуально левее всех остальных. * Самый внешний редекс --- тот, который текстуально не содерж. ни в каком другом. * Самый внутренний --- тот, который в котором не содерж. никакой другой.
Есть два порядка?
* Аппликативный --- выбирается самый левый внутренний. * Нормальный --- берём все самые внешние, выбираем из них самый левый, и его используем.
Здесь мы сначла применили сначала нормальный, потом аппликативный. Теперь можно уточнить:
Следствие из теор. Чёрча-Россера. нормальный порядок редукции приводит к норм. форме за конеч. число шагов, если она вообще есть.
Теперь самое интересное. Если отвлечься от л-выр. и вернуться к прогр., то можно вспомнить, что есть энергинча и ленивая стратегия вычисл. При энерг. мы выч. всё, что только можем. При ленивых выч. мы при виде выр. мы запоминаем его и не вычисляем, пока можно, до тех пор, пока не припрёт. Например:
( ) > 3
Вот тут нам надо вычислить знач. выр., не раньше. Бывает ли такое в языках прогр.? Бывает, но очень редко и по-немногу. Ленивая семантика из компилир. языков --- только хаскель, но все привычные, императивные --- энергичные.
Где можно встретить ленивую модель вычислений? Например, при подст. макросов. Макропроцессору это просто, поск. он работает на уровне текстовых строк. В некоторых командно-скриптовых языках ленивая семантика имеется.
Но сейчас, когда мы смотрим на л-выч., мы видим, что ленивый порядок вычисл. оказался в каком-то виде мощнее.
Введём такую вещб, как понятие связанных и свободных переменных
λ x . x y
Понятно, что x связ., а y --- вободная. Если чуть строже, то построим мн-во FV(E) (free variables(expression)). Как оно вводится:
- FV(x) = {x}
- FV(c) = ∅
- FV(E_1, E_2) = FV(E_1) ∪ FV(e_2)
- FV(λ x . E_1) = FV(E_1) \ {x}
Аналогично можно ввести мн-во Bound variables, BV(E):
- BV(x) = ∅
- BV(c) = ∅
- BV(E_1, E_2) = BV(E_1) ∪ BV(e_2) ; отсюда следует, что прееменная может быт ьи свободная, и связана, но свободна в одной части, а связана в другой
- BV(λ x . E_1) = BV(E_1) ∪ {x}
Выражение, в котором нет связ. переменных, наз. замкнутым. Замкнутыми выр. ещё наз. комбинаторами.
Если x ∉ FV(E), то можно вести речь об η-преобразовании.
Можно заметить, что λ x . E x есть то же самое, что E. Попробуем и то, и другое к a:
E a (λ x . E x) a →β E a
Главное, чтобы в E не было свободной переменной x, иначе ничего не выйдет. Соотв, делаем это преобр.:
E →η λ x. E x
Что оно позв. делать? Например, част. применение встроенных функций. Например, если есть * x y. Является ли * 3 л-выр? Да. А как же с ним работать. Применим η-преобр, получим λ x . * 3 x. Благодаря этому мы можем делать частичное применение функций.
... это называется карринг, по имени учёного Карри (Curry).
Наконец, последнее на сегодня, что же такое Y-combinator. Хочется нам, к примеру, сделать рек. функцию, но как, здесь же нет имён? Мы эту фнкцию получим в кач. второго аргумента. То есть функция получает на фход аргмент и самого себя, и исхитримся и подадим её на вход.
Рассмотрим более идиотический пример --- сумма от 1 до n.
Лектор напишет её сначала на лиспе:
(setq f #'(λ (s x) (if (= x 0) 0 (+ x (funcall s s (- x 1))))))
Что теперь сделать? Нао её вызвать, подав ей на вход число и её саму. Как это сделать?
(funcall f f 5) => 15
можно то же самое сделать и на лямбда-абстракциях
λ s . λ x . COND (= x 0) 0 (+ x (s (- x 1)))
Сущ. неподв. точка, т. е. f(x) = x, и она есть для кажого лямбда-выр.
Есть Y-combinator, который делает:
Y f = f(Y f)
Как выглядит Y-combinator:
Y = λ h . (λ x . h (x x)) (λ x . h (x x))
теперь осталось что?
Y λ s . λ x . COND (= x 0) 0 (+ x (s (- x 1)))
И отредуцировать. Результатом будет функция, от одного арг., выч. сумму.
y-comb. используется в haskell.