Основы Кибернетики, 02 лекция (от 16 февраля)
Материал из eSyr's wiki.
Предыдущая лекция | Следующая лекция
Пример:
- g'(x1, x2, x3, x4): Ng' = {(1111), (1101), (0101), (1010)}
- a = ~x3~x4 v ~x2~x3 v ~x2x4 v ~x1x3 v x2~x4 v ~x1~x4 v ~x1~x2
- пересечение Т = K3 v K4 v K5
- a = ДНФ Квайна
- a1 = K3 v K4 v K5 v K1
- a2 = K3 v K4 v K5 v K2
- ДНФ ΣT = k1 V k2 V k3 V k4 V k5 ≠ a
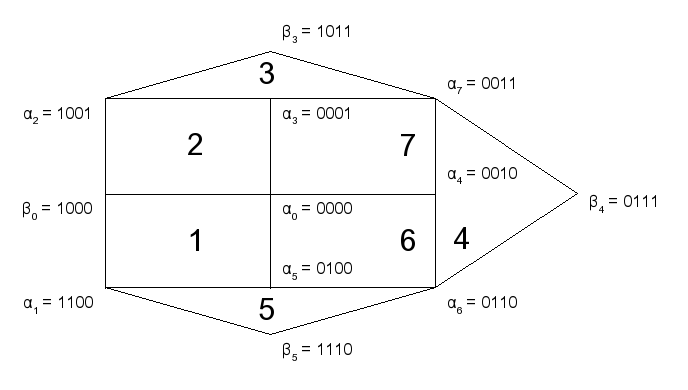
Пусть есть f(x1 ... xn), α ∈ Nf ⇒ Пα(f) — множество проходящих граней f, проходящих через a — пучок f через точку a.
Определение. α ∈ Nf — регулярная точка функции f ⇔ ∃ &betta; ∈ Nf: П&betta;(f) ∈ Пα(f), &betta; не является регулярной.
- П&betta;0(g‘) = {NK1, NK2}
- П&aqlpha0;(g‘) = {NK1, NK2, NK6, NK7}
α0 — регулярная точка g‘
Любая ядровая точка не является регулярной.
α3, α7, α0, α4, α5, α1, α6, α2 — регулярнгые вg‘
Пусть α, α‘ Принадлежат Nk, α — ядровая, α‘ — неядровая ⇒ регулярная
6, 7 состоят только из регулярных точек. Поэтому они являются реглярными гранями.
Грань регулярна ⇔ все её точки регулярны.
Сумма тупиковых соответствует всем нерегулярным граням.
Утверждение 3.2. Простая импликанта K ФАЛ f входит в ДНФ ΣT ⇔ соответствующая ей NK не является регулярной.
Это позволяет строить ДНФ ΣT, не находя все тупиковые ДНФ, а только проверяя все грани на регулярность.
Доказательство. 1) Nk — регулярная грань ⇒ K ∉ ДНФ ΣT
Пусть NK = {α1, ..., αs} ⇒ ∀ αi ∃ &betta;i: П&betta;(f) ∈ П αi(f); &betta;i нерегулярная ⇒ &betta;i ∉ NK ∀ тупиковая ДНФ f покрывает ∀ &betta;i гранью Ni ⇒ Ni ∋ αi
⇒ объединение для i=1, s Ni ∋NK ⇒ K ∉ тупиковая ДНФ
2)Nk — нерегулярная грань ⇒ K ∈ ДНФ ΣT
Возьмём Nf\NK = {&betta;1, ..., &betta;q}
Nk — нерегулярная грань ⇒ ∃ (.) α ∈ NL — нерегулярная (.)
⇒ ∀ j=1..q П &betta;j(f) ∉ Пα(f)
Строгое равенство тоже невозможно, т. к. все точки &betta;i лежат вне грани.
⇒ ∀ j ∃ NKj ∈ П&betta;j(f), NKj ∉ Пαj(f)
⇒ Возьмём ДНФ a = K v K1 v ... v Kq = f
Из неё можно получить тупиковую ДНФ a‘, получающуюся из a удалением граней. Можно ли утверждать, что в эту тупиковую ДНФ войдёт конъюнкция K? Если так и есть, то мы построили ДНФ, в которую входит K, и теорема доказана.
Только K накрывает α Kj не принадлежит пучку альфа, поэтому она альфа не покрывает. Поэтому при переходе к K‘ мы K потерять не можем.
ч.т.д. - первая теорема Журавлёва
[править] Локальность просмотренных методов, алгоритмов, приёмов построения суммы тупиковых ДНФ и тупиковых ДНФ
Определение. Окрестность грани: пусть есть f, NK — максимальная грань функции f. Введём Sr(NK, f) — окрестность порядка r грани NK ФАЛ f, r= N объединение {0}
- S0(NK, f) = NK
- Пусть определено Sr(NK, f). Тогда Sr+1(NK, f) — все те максимальные грани f, которые имеют непустое пересечение хотя бы с одной гранью из окрестности предыдущего порядка (из Sr).
Для того, чтобы понять, является ли NK ядровой (∈ пересечение T(f)), нужно просмотреть S1(NK, f). Как это сформулировать: NK не покрывается (S1(NK, f) \ NK).
Задача. Сформулировать аналогично для ДНФ Квайна, В ДНФ ΣT.
В любом из этих случаев достаточно ограничиваться окрестностью второго порядка. То есть, эти критерии являются локальными.
перечесение M — перечечение минимальных ДНФ ΣM — объединение всех минимальных ДНФ
Для них окрестности второго порядка уже недостаточно.
[править] 4. Особенности ДНФ для ФАЛ из некоторых классов (линейные ФАЛ, монотонные ФАЛ и др.). Теореме Журавлёва о ДНФ ΣM (2-я теор Журавлёва)
Линейная функция — f(x1, ..., xn) = α1x1 &xor; ... αnxn &xor &alpha0
xi — существенная булева переменная f ⇔ αi = 1
ln(x1, ..., xn) = x1 &xor; ... &xor; xn ⇒ Nln = Bn нечётные ~ln(x1, ..., xn) = x1 &xor; ... &xor; xn &xor; 1 ⇒ N~ln = Bn чётные
Рассмотрим ДНФ этих функций.
(α1 ... αi−1, 0, αi+1 ... αn) = α, (α1 ... αi−1, 1, αi+1 ... αn) = &betta; — соседние наборы
Пусть в Nf нет соседних по xi наборов. ⇒ в ∀ импликанту KФАЛ f входит либо xi, либо ~xi. Рис 2 Если от xi не зависит, то при изменении xi мы попадаем в ту же грань, так как значение функции она не меняет.
В ln, ~ln соседних наборов в Nf нет. То есть, все грани имеют размерность 0. То есть, совершенная ДНФ является единственной ДНФ для этих функций.
Утверждение 4.1. Совершенная ДНФ ФАЛ f ∈ P2(n) является её единственной ДНФ от x1 ... xn ⇔ в Nf нет соседних наборов.
Доказательство. 1) Если в Nf нет соседних наборов, тогда получается, что любая импликанта содержит все переменные, тогда она соответствует грани размерности 0, сама импликанта функции f имеет ранг n ⇔ Совершенная ДНФ — единственная ДНФ ФАЛ f 2) Пусть α, &betta;, — сосдние по xi точки в Nf ⇔ a1 — Совершенная ДНФ f, a2 — ДНФ K v Cов ДНФ(g), Ng = Nf{α, &betta}, Nk = {α, &betta} чтд
Следствие. ln, ~ln имеют сов ДНФ — единственная ДНФ от x1 ... xn.
Монотонная ДНФ. У неё одна тупиковая ДНФ, совпадает с сокращённой ДНФ.
Пусть f(x1...xn) монотонно зависит от xi ⇔ ∀ (α1 ... αi−1, 0, αi+1 ... αn) = α, (α1 ... αi−1, 1, αi+1 ... αn) = &betta; ⇔ f(α) <= f(&betta;)
f(x1...xn) – монот ФАЛ ⇔ f монот по &forall xi ⇔ ∀ α <= &betta; ⇒ f(α) <= f(&betta;)
Пусть f(x1...xn) монотонно зависит от xi ⇒ ~xi не входит в простые импликанты f.
Пусть K‘ = ~xi: K‘ — импликанта f ⇒ NK‘ &in= Nf ⇒ K‘‘ = xiK, K – импликанта f !! ⇒ K‘ не явл простой импликантой
f(x1...xn) – монот ФАЛ ⇒ любая простая импликанта не содержит отрицаний переменных ⇒ монот элементарные конъюнкции
Пусть &betta; = (0...01(позиция i1)0...01(позиция i2)0..01(позиция ir)0...0) ⇒ K_&betta;^+ (x1...xn)= xi1xi2...xir
⇒ K_&betta;(x1...xn) = xi1...xir~xj1...~xjt
Возьмём K&betta;‘+ <= K&bettal;‘‘+ ⇔ NK&betta;‘+ <= NK&bettal;‘‘+ K&betta;‘+ <= K&bettal;‘‘+ ⇒ &betta;‘ >= &betta;‘‘ ⇒ &betta;‘ ∈ NK&betta;‘‘+
f — монот ФАЛ. Тогда α — «нижняя» 1 f ⇔ α ∈ Nf и ∀ &betta; <= α, &betta; != α ⇔ f(b) = 0 ⇒ Nf+ — множество всех нижних «1» монотонных ФАЛ f
4.2 Сокр ДНФ a монот ФАЛ f является единств тупик ДНФ и имеет вид a = V_&betta; ∈ Nf+ K_&betta;^+, причём все наборы из Nf+ являются ядровыми точками f, и все max грани — ядр. гранями.
Это следует из указанного выше свойства.
- ∀ простая импликанта f = K&betta;+ ---> NK&betta;+ — максимальная грань ⇒ &betta; ∈ Nf+
- &betta; *in; Nf+ ⇒ K&betta;+ — простая импликанта f ⇒ ∃ простая импликанта K&betts;‘+ ⇒ &betta;‘ <= != &betta; ⇒ &betta; ∉ Nf+ ??!!
Пример: функция голосования. Сокр ДНФ H = x1x2 v x1x3 v x2x3
последнее семейство функций, которые мы рассмотрим: цепные или циклические функции. На единичном кубе их еж значения состоят из рёбер, которые организуют циклы.
f ∈ P2(n) — цепная (циклическая) ФАЛ длины t ⇔ Сокр ДНФ f представляет собой цепь (цикл) из t рёбер куба Bn.
Для куба размерности m змея примерно длины ¼ 2^m
∀ t ∃ n: в P2(n) ∃ цепная ФАЛ длины t
Огрнаичения на t для циклической:
- 3, 4 быть не может
- t чётная
Пусть f — цепная ф-ция длины t, t >= 4
1)Сокр ДНФ = ДНФ Квайна = ДНФ ΣT (Утверждение 3.1) 2)t = 2k – 1 ⇒ ∃ единств min ДНФ N1 объединение N2 объединение ... Nt 3)t = 2k ⇒ f‘ и f‘‘ — цепные ФАЛ длины 2k − 1 Nf‘ = Nf\{α1}; Nf‘‘ = Nf\{αt} ⇒ ∀ Ni ∈ min ДНФ только f‘ или f‘‘
⇒ Sk−2(Nk, f‘) = Sk−2(Nk, f‘‘)
4.3 ∀ n в P2(n) ∃ f‘ и f‘‘ имеющие общую простую импликанту K, которая входит в ДНФ ΣM одной f‘, f‘‘ и не входит в ДНФ ΣM другой и Sn−3(NK, f‘) = Sn−3(NK, f‘‘)
Докво. Строим в P2(n) цепную ФАЛ длины (2n − 2) = 2k ⇒ Sk−2(Nk, f‘) = Sk−2(Nk, f‘‘) (100..0), (1100.0), ... (1...1)(01...1)...(0...01)
Задачи для самостоятельного решения. Принести в 617. Кто-то из преподавателей должен зафиксировать дату и время и оставить в папке для лектора. Тот, кто первый решит, освобождается от задачи на ДНФ.
1. Построить функцию с минимальным числом булевских переменных, длина сокращённой ДНФ которой превосходит длину соврешенной ДНФ этой же функции. 2. Построить функцию с минимальным числом булевских переменных, ни одна кратчайшая ДНФ не является минимальной ДНФ и ни одна минимальная не является кратчайшей.
01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16
Календарь
| пт | пт | пт | пт | пт | |
Февраль
| 09 | 16 | 26 | ||
Март
| 02 | 09 | 16 | 23 | 30 |
Апрель
| 06 | 13 | 20 | 27 | |
Май
| 04 | 11 | 18 | 25 |
Материалы к экзамену
Экзаменационные вопросы 3 потока 2007 (new!) | Алгоритмы решения задач | Теормин | Определения