МОТП, Билеты (2009)

Материал из eSyr's wiki.

Версия от 13:02, 24 июня 2012; 89.249.164.135 (Обсуждение)

(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)

Содержание

1 Часть 1 (Ветров)
2 Часть 2 (Рудаков)

[править] Часть 1 (Ветров)

[править] Метод максимального правдоподобия. Его достоинства и недостатки

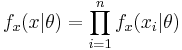Метод максимального правдоподобия — метод оценивания неизвестного параметра путём максимизации функции правдоподобия: $f_x (x|\theta) = \prod_{i=1}^n f_x(x_i | \theta)$ для независимой выборки n величин.

Недостатки:

нужно знать априорное распределение (с точностью до параметров) наблюдаемой величины
хорошо применим при допущении, что 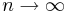$n \rightarrow \infty$ (асимптотически оптимален), что в реальности не так
проблема выбора структурных параметров, позволяющих избегать переобучения (проблема вообще всех методов машинного обучения)
необходима регуляризация метода

[править] Решение несовместных СЛАУ

В статистике, машинном обучении и теории обратных задач под регуляризацией понимают добавление некоторой дополнительной информации к условию с целью решить некорректно поставленную задачу или предотвратить переобучение.

Несовместная СЛАУ — система линейных уравнений, не имеющая ни одного решения.

Совместная СЛАУ — система линейных уравнений, имеющая хотя бы одно решение.

Ридж-регуляризация (ридж-регрессия, регуляризация Тихонова) матрицы

A T A

— матрица

A T A + λ I

, где

λ

— коэффициент регуляризации. Всегда невырождена при

λ > 0

Нормальное псевдорешение СЛАУ

A x = b

— вектор

x = (A T A + λ I) - 1 A T b

всегда единственно
при небольших $λ$ определяет псевдорешение с наименьшей нормой
любое псевдорешение имеет минимальную невязку

[править] Задача восстановления линейной регрессии. Метод наименьших квадратов

Задача регрессионного анализа (неформально): предположим, имеется зависимость между неизвестной нам случайно величиной X (мы судим о ней по наблюдаемым признакам, т.е. по случайной выборке) и некоторой переменной (параметром) t.

Задача регрессионного анализа — определение наличия и характера (математического уравнения, описывающего зависимость) связи между переменными. В случае линейной регрессии, зависимость X от параметра t проявляется в изменении средних значений Y при изменении t (хотя при каждом фиксированном значении t величина X остается случайной величиной).

Искомая зависимость среднего значения X от значений Z обозначается через функцию f(t): $E (X | Z = t) = f (t)$ . Проводя серии экспериментов, требуется по значениям t₁, …, t_n и X₁, …, X_n оценить как можно точнее функцию f(t).

Однако, наиболее простой и изученной является линейная регрессия, в которой неизвестные настраиваемые параметры (w_j) входят в решающее правило линейно с коэффициентами $ψ j (x)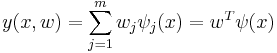$ : $y(x,w)=\sum_{j=1}^m w_j \psi_j(x)=w^T \psi(x)$ /

Пример (простой пример на пальцах): Linear Regression Example.

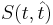$S(t, \hat{t})$ — функция потерь от ошибки. На пальцах: берем найденную путем регрессии функцию 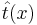$\hat{t}(x)$ и сравниваем её выдачу на тех же наборах $x$ , что и заданные результаты эксперимента $t (x)$ .

$S_1(t, \hat{t}) = (t - \hat{t})^2$
$S_2(t, \hat{t}) = |t - \hat{t}|$
$S_3(t, \hat{t}) = \delta^{-1}(t - \hat{t})$

Основная задача — минимизировать эту функцию, что значит минимизировать 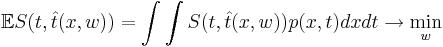$\mathbb{E} S(t, \hat{t}(x,w)) = \int\int S(t, \hat{t}(x,w)) p(x,t) dx dt \rightarrow \min_{w}$ .

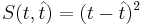Метод наименьших квадратов — минимизация функции потери ошибки $S(t, \hat{t}) = (t - \hat{t})^2$ .

Особенности квадратичной функции потерь:

Достоинтсва:
- Гладкая (непрерывная и дифференцируемая);
- Решение может быть получено в явном виде.
Недостатки:
- Решение неустойчиво;
- Не применима к задачам классификации.

[править] Задача восстановления линейной регрессии. Вероятностная постановка

Представим регрессионную переменную как случайную величину с плотностью распределения $p (t | x)$ .

В большинстве случаев предполагается нормальное распределение относительно некоторой точки y(x): 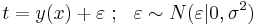$t = y(x) + \varepsilon~;~~\varepsilon \sim N(\varepsilon | 0, \sigma^2)$ .

Максимизируя правдоподобие (оно задается следующей формулой: 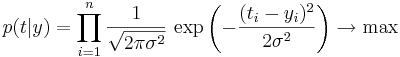$p(t|y)=\prod_{i=1}^n \dfrac{1}{\sqrt{2\pi\sigma^2}}\, \exp\left(-\dfrac{(t_i-y_i)^2}{2\sigma^2}\right) \rightarrow \max$ ), получаем эквивалентность данного метода методу наименьших квадратов, т. к. взяв логарифм от формулы выше, получаем:

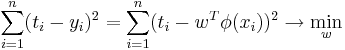
$\sum_{i=1}^n (t_i-y_i)^2 = \sum_{i=1}^n (t_i-w^T \phi (x_i))^2 \rightarrow \min_w$

[править] Логистическая регрессия. Вероятностная постановка

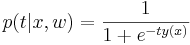Логистическая регрессия (en-wiki, machinelearning) — метод классификации объектов на два класса, работающий при помощи логистической функции регрессии: $p(t|x, w) = \frac{1}{1 + e^{-t y(x)}}$ (сигмоид).

Эта функция является функцией правдоподобия по w и распределением вероятности по t, т.к. 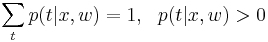$\sum_t p(t|x,w)=1, \ \ p(t|x,w)>0$ .

[править] ЕМ-алгоритм для задачи разделения гауссовской смеси

Пусть имеется выборка 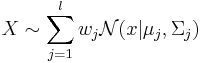$X \sim \sum_{j=1}^l w_j \mathcal{N} (x | \mu_j , \Sigma_j)$ , где l - число компонент смеси.

EM-алгоритм: (en-wiki], machinelearning-пример)

Выбираем начальное приближение для параметров $\mu_j, \Sigma_j, w_j, j \isin [1, l]$ .
E-шаг (expectation): находим для каждого элемента выборки вероятность, с которой он принадлежит каждой из компонент смеси.
M-шаг (maximization): с учетом вероятностей на предыдущем шаге пересчитываем коэффициенты начального шага.
Переход к E шагу до тех пор, пока не будет достигнута сходимость.

Недостатки:

(!) Не позволяет определить количество компонент смеси (l).
- Величина l является структурным параметром.
В зависимости от выбора начального приближения может сходиться к разным точкам.
может сваливаться в локальный экстремум.

[править] Основные правила работы с вероятностями. Условная независимость случайных величин

Случайная величина — это измеримая функция, заданная на каком-либо вероятностном пространстве. (ru.wiki)

Функция распределения

F X (x)

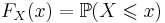— вероятность того, что случайная величина X меньше x: $F_X(x) = \mathbb{P}(X \leqslant x)$ .

Плотность вероятности :

В дискретном случае — вероятность того, что X = x;
В непрерывном случае — производная функции распределения.

Далее X, Y — случайные величины с плотностями вероятности $p (x), p (y)$ .

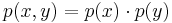Случайные величины X, Y называются независимыми, если $p(x,y) = p(x) \cdot p(y)$ .

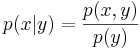Условная плотность — $p(x|y) = \frac{p(x,y)}{p(y)}$ .

в дискретном случае — вероятность того, что наступило событие x, при условие наступления события y.

Правило суммирования: пусть $A_1, \dots, A_k$ — k взаимоисключающих события, одно из которых обязательно наступает. Тогда

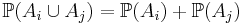
$\mathbb{P}(A_i \cup A_j) = \mathbb{P}(A_i) + \mathbb{P}(A_j)$
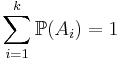
$\sum_{i=1}^k \mathbb{P}(A_i) = 1$
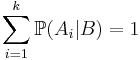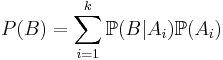Формула полной вероятности: $\sum_{i=1}^k \mathbb{P}(A_i|B) = 1$ или $P(B)=\sum_{i=1}^k \mathbb{P}(B|A_i) \mathbb{P}(A_i)$ .
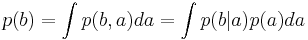В интегральном виде: $p(b) =\int p(b,a)da=\int p(b|a)p(a)da$ .
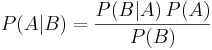Формула Байеса (ru:wiki): $P(A|B) = \frac{P(B | A)\, P(A)}{P(B)}$ .

Случайные величины называются условно независимыми от $z$ , если $p (x, y | z) = p (x | z) p (y | z)$

Это значит: вся информация о взаимосвязи между $x$ и $y$ содержится в $z$ .
Из безусловной независимости не следует условная независимость.
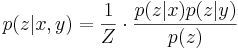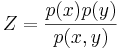Основное свойство условно независимых величин: $p(z|x,y) = \frac{1}{Z} \cdot \frac{p(z|x) p(z|y)}{p(z)}$ , где $Z = \frac{p(x)p(y)}{p(x,y)}$ .

[править] Графические модели. Основные задачи, возникающие в анализе графических моделей

Графическая модель -- ориентированный или неориентированный граф, в котором вершины соответствуют переменным, а ребра - вероятностным отношениям, определяющим непосредственные зависимости.

Пусть $X$ -- совокупность наблюдаемых переменных, $T$ -- ненаблюдаемых.

Основные задачи:

подсчёт условного распределния на значениях отдельной скрытой переменной: $p (t i | X)$
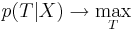
нахождение наиболее вероятной конфигурации скрытых переменных при заданных наблюдаемых значениях: $p(T|X) \rightarrow \max_T$
оценка адекватности выбранной графической модели данным $p (X)$

[править] Байесовские сети. Примеры.

Байесовская сеть — это вероятностная модель, представляющая собой множество переменных и их вероятностных зависимостей.

(wiki: опред., принципы и пример) + см. презентации

Особенности:

По смыслу построения байесовские сети не могут содержать ориентированные циклы, т.к. это будет нарушать правило умножения вероятностей
Главным достоинством графических моделей является относительно простое выделение условно-независимых величин, которое облегчает дальнейший анализ, позволяя значительно уменьшить количество факторов, влияющих на данную переменную

[править] Марковские сети. Примеры.

[править] Скрытые марковские модели. Обучение СММ с учителем.

Скрытая Марковская модель (первого порядка) — это вероятностная модель последовательности, которая:

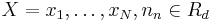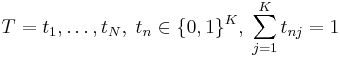состоит из набора наблюдаемых переменных $X = {x_1 , \dots , x_N }, n_n \in R_d$ и латентных (скрытых) переменных $T = {t_1, \dots, t_N },\;t_n \in \{0, 1\}^K,\;\sum_{j = 1}^{K}t_{nj}=1$ .
латентные переменные T являются бинарными и кодируют K состояний, поэтому их иногда называют переменными состояния.
значение наблюдаемого вектора $x n$ , взятого в момент времени $n$ , зависит только от скрытого состояния $t n$ , которое в свою очередь зависит только от скрытого состояния в предыдущий момент времени $t n - 1$ .
для полного задания модели достаточно задать все условные распределения вида 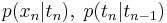$p(x_n |t_n ),\;p(t_n |t_{n-1})$ и априорное распределение $p (t 1)$ .

Пусть имеется $K$ возможных состояний. Закодируем состояние в каждый момент времени $n$ бинарным вектором 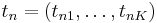$t_n = (t_{n1},\dots, t_{nK})$ , где $t n j = 1$ , если в момент $n$ модель находится в состоянии $j$ и $t n j = 0$ , иначе.

Тогда распределение $p (t n | t n - 1)$ можно задать матрицей перехода $A$ размера $K \times K$ , где

A_ij = p(t_nj = 1 \| t_{n − 1,i} = 1),	∑	A_ij = 1
	j

, т.е. 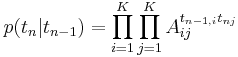$p(t_n |t_{n-1}) = \prod_{i=1}^K\prod_{j=1}^K A_{ij}^{t_{n-1,i}t_{nj}}$ Пусть в первый момент времени $p (t 1 j = 1) = π j$ . Тогда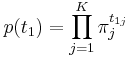 $p(t_1) = \prod_{j=1}^K \pi_j^{t_{1j}}$

Хотя матрица A может быть произвольного вида с учетом ограничений на неотрицательность и сумму элементов строки, с точки зрения СММ представляет интерес диагональное преобладание матрицы перехода.
В этом случае можно ожидать, что процесс находится в некотором состоянии на протяжении какого-то отрезка времени.
Появляется простая физическая интерпретация СММ: имеется процесс, который иногда (относительно редко) скачкообразно меняет свои характеристики.

Условное распределение $p (x n | t n)$ определяется текущим состоянием $t n$
Обычно предполагают, что оно нам известно с точностью до параметров 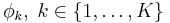$\phi_k,\;k \in \{1,\dots, K\}$ , т.е. если $t n 1 = 1$ , то $x n$ взят из распределения $p (x n | φ 1)$ , если $t n 2 = 1$ , то $x n$ взят из распределения $p (x n | φ 2)$ , и т.д.
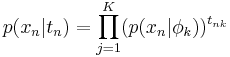
Таким образом $p(x_n |t_n) = \prod_{j=1}^K(p(x_n |\phi_k ))^{t_{nk}}$

Обозначим полный набор параметров $Θ = {π, A,φ}$ .

Обучение с учителем. Известна некоторая последовательность $X$ , для которой заданы $T$ . Задача состоит в оценке по обучающей выборке набора параметров $Θ$ .

[править] Алгоритм динамического программирования и его применение в скрытых марковских моделях.

см. Лекция 3, стр. 9-28

Динамическое программирование в математике и теории вычислительных систем — метод решения задач с оптимальной подструктурой и перекрывающимися подзадачами, который намного эффективнее, чем решение «в лоб». (дин. прогр. на вики)

Собственно, билет.

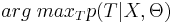Пусть известна некоторая последовательность наблюдений $X$ и набор параметров СММ $Θ$ . Требуется определить наиболее вероятную последовательность состояний $T$ , т.е. найти $arg\;max_T p(T|X, \Theta)$ .
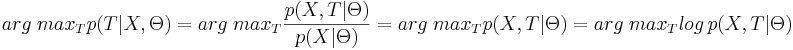Заметим, что $p (X | Θ)$ не зависит от $T$ , поэтому $arg\;max_T p(T|X, \Theta) = arg\;max_T \frac{p(X, T|\Theta)}{p(X|\Theta)} = arg\;max_T p(X, T|\Theta) = arg\;max_T log\,p(X, T|\Theta)$ .
Но это же классическая задача динамического программирования!

Алгоритм Витерби (Алгоритм Витерби на вики - очень хорошо для понимания зачем все это надо)

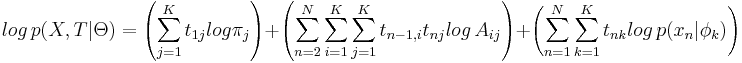
Логарифм совместной плотности по распределению: $log\,p(X, T|\Theta) = \left(\sum_{j=1}^K t_{1j}log\pi_j\right) + \left(\sum_{n=2}^N\sum_{i=1}^K\sum_{j=1}^K t_{n-1,i}t_{nj}log\,A_{ij}\right) + \left(\sum_{n=1}^N\sum_{k=1}^K t_{nk}log\,p(x_n|\phi_k)\right)$

Функция Беллмана 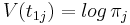$V(t_{1j}) = log\,\pi_j$
$V(t_{nj}) = max_i \left[ V(t_{n-1,i}) + \left(\sum_{i=1}^K\sum_{j=1}^K t_{n-1,i}t_{nj}log\,A_{ij}\right) + log\,p(x_n, \phi_j)\right]$
$S(t_{nj}) = arg\;max_i \left[ V(t_{n-1,i}) + \left(\sum_{i=1}^K\sum_{j=1}^K t_{n-1,i}t_{nj}log\,A_{ij}\right) + log\,p(x_n, \phi_j)\right]$

Выполнив прямой проход по сигналу, мы оцениваем $V (t n j)$ и $S (t n j)$ , а выполнив обратный проход, мы получаем оптимальные номера оптимальных состояний 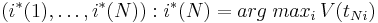$(i^\ast(1),\dots, i^\ast(N)): i^\ast(N) = arg\;max_i\,V(t_{Ni})$
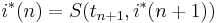
$i^\ast(n) = S(t_{n+1},i^\ast(n+1))$

Легко видеть, что значения переменных $t n$ определяются так: 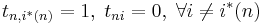$t_{n,i^\ast(n)} = 1,\;t_{ni} = 0,\;\forall{}i \neq i^\ast(n)$

[править] ЕМ-алгоритм и его применение в скрытых марковских моделях.

[править] Максимум неполного правдоподобия

Предположим имеется графическая модель в которой известная только часть значений переменных.
Атомарные распределения известны с точностью до $θ$
Требуется оценить параметры по наблюдаемым величинам с помощью метода максимального правдоподобия т.е найти $θ M L = argmax(p (X | θ))$
По правилу суммирования вероятностей неполное правдоподобие может быть получено в виде суммирования по скрытым переменным полного правдоподобия

p(X \| θ) =	∑	p(X,T \| θ)
	T

Во многих случаях(в частности в байесовских сетях) подсчет полного правдоподобия тривиален
При оптимизации правдоподобия удобно переходить к логарифму, в частности ранее в курсе мы получили явные формулы для $argmax θ (p (X | θ) = argmax θ l o g (p (X | θ)$ в СММ
Прямая оптимизация логарифма неполного правдоподобия очень затруднительн, даже в итерационной форме, т.к. фунционал имеет вид "логарифма суммы",в то время как удобно оптимизировать "сумму логарифов".

[править] Схема ЕМ-алгоритма

на входе: выборка X, зависящая от набора параметров $θ$
Инициализируем $θ$ некоторыми начальным приближением
Е-шаг: оцениваем распределение скрытой компоненты

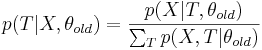
$p(T|X,\theta_{old})=\frac{p(X|T,\theta_{old})}{\sum_T p(X,T|\theta_{old})}$

M-шаг оптимизируем

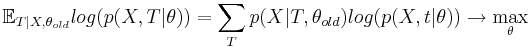
$\mathbb E_{T|X,\theta_{old}} log(p(X,T|\theta))=\sum_T p(X|T,\theta_{old})log( p(X,t|\theta)) \to \max_{\theta}$
Если бы мы точно знали значение $T = T 0$ , то вместо мат. ожидания по всевозможным(с учетом наблюдаемых данных) $T | X,θ o l d$ мы бы оптимизировали $l o g (p (X, T 0 | θ))$

Переход к E-шагу пока процесс не сойдется
Оптимизация проводится итерационно методом покоординатного спуска: на каждой итерации последовательно уточняются возможные значения Т (Е-шаг), а потом пересчитываются значения $θ$ (М-шаг)
Во многих случаях на М-шаге можно получить явные формулы, т.к. там происходит оптимизация выпуклой комбинации логарифмов полных правдоподобий, имеющей вид взвешенной "суммы лоагрифмов"

[править] EM-алгоритм для смеси гауссовских распределений

см. пункт 1.6 недостатки:

В зависимости от выбора начального приближения может сходится к разным точкам
ЕМ-алгоритм находит локальный экстремум, в котором значение правдоподобия может оказаться намного ниже, чем в глобальном варианте
ЕМ-алгоритм не позволяет определить количество компонентов смеси l
!!Величина l является структурным параметром(в начале лекций говорилось о них)

[править] Условная независимость в скрытых марковских моделях. Алгоритм «вперед-назад».

Лекция 4, Слайды 16-28
вики

Алгоритм «вперёд-назад» -- алгоритм для вычисления апостериорных вероятностей последовательности состояний при наличии последовательности наблюдений. Или по другому, алгоритм для того, чтобы вычислить вероятность специфической последовательности наблюдений. Это работает в контексте скрытых Марковских моделей.

работает за линейное по количеству наблюдаемых переменных ( $N$ )

Алгоритм включает три шага:

вычисление прямых вероятностей
вычисление обратных вероятностей
вычисление сглаженных значений

[править] Метод релевантных векторов в задаче восстановления регрессии.

Лекция 5 Ветров.

[править] Метод релевантных векторов в задаче классификации.

Лекция 5 Ветров.

Еще слайды Ветрова, но не из этого круса от того более понятными не становятся

[править] Метод главных компонент.

Пусть имеется некоторая выборка 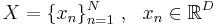$X = \{x_n\}_{n=1}^N~,~~ x_n \in \mathbb{R}^D$ . Цель -- представить выборку в пространстве меньшей размерности $d < D$ таким образом, чтобы в новом пространстве "схожие" объекты образовывали компактные области.

PCA (Principal Component Analysis) -- Метод главных компонент. Формулировки:

проекция данных на гиперплоскость с наименьшей ошибкой проектирования
поиск проекции на гиперплоскость с сохранением большей части дисперсии в данных

Википедия: Метод главных компонент

[править] Вероятностная формулировка метода главных компонент.

Метод главных компонент можно сформулировать в виде вероятностной модели со скрытыми переменными, для оптимизации которой используем метод максимального правдоподобия.

Преимущества:

вычисление правдоподобия на тестовой выборке позволяет сравнивать различные вероятностные модели
EM-алгоритм позволяет быстро находить решения в случае малого количества главных компонент
EM-алгоритм позволяет избежать вычисление матрицы ковариации на промежуточном шаге
возможность автоматического определения числа главных компонент

Вероятностная модель:

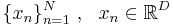
Пусть имеется выборка $\{x_n\}_{n=1}^N~,~~ x_n \in \mathbb{R}^D$
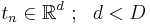
для каждого объекта $x n$ рассмотрим скрытую переменную $t_n \in \mathbb{R}^d~;~~d < D$
определим распределение скрытых переменных 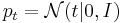$p_t = \mathcal{N}(t|0, I)$ (многомерное нормальное распределение)
Таким образом, модель наблюдаемой переменной x представляет собой линейное преобразование с добавлением гауссовского шума: 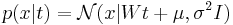, где
- $W \in \mathbb{R}^{D \times d}$
- $\mu \in \mathbb{R}^D$

[править] ЕМ-алгоритм в методе главных компонент. Его преимущества.

[править] Метод главных компонент. Схема автоматического выбора числа главных компонент.

[править] Недостатки метода главных компонент. Метод независимых компонент.

Лекция 6, слайды 42-46

Недостатки метода главных компонент:

возможны только линейные подпространства, объясняющие данные с высокой точностью. на практике часто такие поверхности могут быть сложными криволинейными.
PCA инвариантен относительно поворота. это значит, что восстановление скрытых переменных неоднозначно. Это плохо в случае, если имеется несколько независимых источников, которые представимы линейной смесью с неизвестными коэффициентами

Метод независимых компонент -- направлен на разрешение второй проблемы PCO.

пусть наблюдаемые переменные являются линейной комбинацией скрытых переменных, причем кол-во наблюдаемых и скрытых переменных совпадает: $x = W t$
если $W$ невырождена, то $t = W - 1 x$

Суть метода:

рассматриваем отдельно каждый источник
для каждого источника ищем ее, как линейную комбинацию наблюдаемых данных
по Центральной предельной теореме сумма случайный величин приближается к нормальному распределению. А так как у нас не случайные величины, то нам нужно искать решение, которое меньше всего похоже на гауссиану

[править] Нелинейные методы уменьшения размерности. Локальное линейное погружение.

Лекция 6, слайды 48-50

PCA не позволяет находить преобразования, которые основаны на том факте, что близкие объекты на некоторой поверхности, были бы близки и в новом пространстве. то есть все наши наблюдения сосредотачиваются на некоторой (совсем не факт, что линейной) поверхности. Задача - восстановить эту поврехность

LLE ( локальное линейное погружение ) -- метод, основанный на поиске преобразования с учётом сохранения отношения соседства между объектами

[править] Нелинейные методы уменьшения размерности. Ассоциативные нейронные сети и GTM.

Лекция 6, слайды 51-55

[править] Часть 2 (Рудаков)

[править] Объекты, признаки, логические признаки, простейшие логические решающие правила.

Признаки объектов:

детерминированные;
вероятностные;
логические;
структурные.

Детерминированные признаки – это признаки, принимающие конкретные числовые значения, которые могут быть рассмотрены как координаты точки, соответствующей данному объекту, в n-мерном пространстве признаков.

Вероятностные признаки – это признаки, случайные значения которых распределены по всем классам объектов, при этом решение о принадлежности распознаваемого объекта к тому или другому классу может приниматься только на основании конкретных значений признаков данного объекта, определенных в результате проведения соответствующих опытов. Признаки распознаваемых объектов следует рассматривать как вероятностные и в случае, если измерение их числовых значений производится с такими ошибками, что по результатам измерний невозможно с полной определенностью сказать, какое числовое значение данная величина приняла.

Логические признаки распознаваемых объектов можно рассматривать как элементарные высказывания, принимающие два значения истинности (истина – ложь) с полной определенностью. К логическим признакам относятся прежде всего признаки, не имеющие количественного выражения. Эти признаки представляют собой суждения качественного характера типа наличия или отсутствия некоторых свойств или некоторых элементов у распознаваемых объектов или явлений. В качестве логических признаков можно рассматривать, например, такие симптомы в медицинской диагностике, как боль в горле, кашель и т.д. К логическим можно отнести также признаки, у которых важна не величина признака у распознаваемого объекта, а лишь факт попадания или непопадания ее в заданный интервал. В пределах этих интервалов появление различных значений признаков у распознаваемых объектов предполагается равновероятным. На практике логические признаки подобного рода имеют место в таких ситуациях, когда либо ошибками измерений можно пренебречь, либо интервалы значений признаков выбраны таким образом, что ошибки измерений практически не оказывают влияния на достоверность принимаемых решений относительно попадания измеряемой величины в заданный интервал.

Решающее правило Decision Rule

В Data Mining это правила вида «Если …, то…», которые позволяют принять решение о принадлежности объекта или наблюдения к определенному классу, например, «Если ‘Годовой доход’ больше 200000, то ‘Кредитный рейтинг’ = ‘Высокий’. Основное применение решающих правил – деревья решений. В каждом узле дерева решений содержится решающее правило, разбивающее множество примеров в узле на подмножества, ассоциированные с классами.

Кроме этого, решающие правила применяются в методах покрытия, когда формируются наборы правил, которые последовательно относятся ко всем наблюдениям.

Остаток можно взять из файла lekcii_ama_zhuravlev.doc страница 17.

[править] Проблемы формирования логических признаков. Оценки качества признаков и их совокупностей.

Пусть 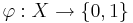$\varphi : X \rightarrow \{0, 1\}$ - некоторый предикат, определённый на множестве объектов X. Говорят, что предикат 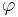$\varphi$ выделяет или покрывает (cover) объект x, если 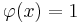$\varphi(x) = 1$ . Предикат называют закономерностью, если он выделяет достаточно много объектов какого-то одного класса $c$ , и практически не выделяет объекты других классов.

Пример: Решается вопрос о целесообразности хирургической операции. Закономерность: если возраст пациента выше 60 лет и ранее он перенёс инфаркт, то операцию не делать - риск отрицательного исхода велик.

Всякая закономерность классифицирует лишь некоторую часть объектов. Объединив определённое количество закономерностей в композицию, можно получить алгоритм, способный классифицировать любые объекты. Логическими алгоритмами классификации будем называть композиции легко интерпретируемых закономерностей. При построении логических алгоритмов возникают три основных вопроса:

Каков критерий информативности, позволяющий называть предикаты закономерностями?
Как строить закономерности?
Как строить алгоритмы классификации на основе закономерностей? Наиболее распространённые типы логических алгоритмов: Голосование правил (алгоритм Кора), Алгоритмы вычисления оценок.

Теперь поговорим об информативности (или качестве) признака. Своими словами: предикат 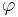$\varphi$ тем более информативен, чем больше он выделяет объектов "своего класса" 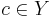$c \in Y$ по сравнению с объектами всех остальных "чужих" классов. Свои объекты называют также позитивными (positive), а чужие негативными (negative). Введём следующие обозначения:

$P c$ - число объектов класса c в выборке X
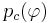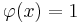$p_c(\varphi)$ - из них число объектов, для которых выполняется условие $\varphi(x) = 1$ ;
$N c$ - число объектов всех остальных классов Y \ {c} в выборке X
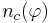$n_c(\varphi)$ - из них число объектов, для которых выполняется условие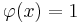 $\varphi(x) = 1$

Введем ещё два обозначения:

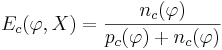$E_c ( \varphi , X ) = \frac {n_c(\varphi)}{p_c(\varphi)+ n_c(\varphi)}$ - доля негативных объектов среди всех выделяемых объектов (доля тех объектов, в которых наш логический предикат ошибся - причислил их к "своему" классу, хотя они туда и не относились)
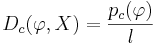$D_c ( \varphi , X ) = \frac {p_c(\varphi)}{l}$ , где l есть это количество элементов в выборке X - это доля выделенных позитивных объектов.

Существует несколько способов определения информативности: статическое определение, энтропийное. Также существует такое понятие как многоклассовая информативность, когда приходится оценивать информативность не только таких предикатов, которые отделяют один класс от остальных, но и таких, которые отделяют некоторую группу классов от остальных.

[править] Методы голосования по конъюнкциям. Алгоритмы типа "Кора".

Для начала, поговорим об алгоритмах голосования. Пусть для каждого класса 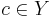$c \in Y$ построено множество логических закономерностей (правил), специализирующихся на различении объектов данного класса: 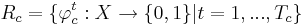$R_c = \{ \varphi_c^t : X \rightarrow \{0, 1\} | t = 1, . . . , T_c\}$ , где $T c$ - количество классов свойств.

Считается, что если 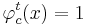$\varphi_c^t (x) = 1$ , то правило 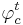$\varphi_c^t$ относит объект 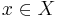$x \in X$ к классу c. Если же 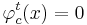$\varphi_c^t(x) = 0$ , то правило 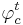$\varphi_c^t$ воздерживается от классификации объекта x.

Алгоритм простого голосования
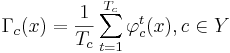
- подсчитывает долю правил в наборах $R c$ , относящих объект x к каждому из классов: $\Gamma_c(x) = \frac 1 {T_c} \sum_{t=1}^{T_c} \varphi_c^t (x) , c \in Y$
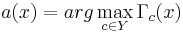
- относит объект x к тому классу, за который подана наибольшая доля голосов: $a(x) = arg \max_{c \in Y} \Gamma_c (x)$
- если максимум достигается одновременно на нескольких классах, выбирается тот,

для которого цена ошибки меньше.

Алгоритм взвешенного голосования
- Каждому правилу 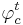$\varphi_c^t$ приписывается вес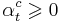 $\alpha_t^c \geqslant 0$
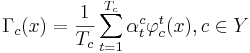
- при голосовании берётся взвешенная сумма голосов: $\Gamma_c(x) = \frac 1 {T_c} \sum_{t=1}^{T_c} \alpha_t^c \varphi_c^t (x) , c \in Y$
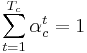
- веса принято нормировать на единицу: $\sum_{t=1}^{T_c} \alpha_c^t = 1$

При построении алгоритмов взвешенного голосования правил возникает четыре основных вопроса:

Как построить много правил по одной и той же выборке?
Как избежать повторов и построения почти одинаковых правил?
Как избежать появления непокрытых объектов и обеспечить равномерное покрытие всей выборки правилами?
Как определять веса правил при взвешенном голосовании?

Алгоритм Кора

Дано
- множество элементарных предикатов $Β$
- обучающая выборка X
Хотим получить
- набор конъюктивных закономерностей (т.е. множество конъюнкций элементарных предикатов $Β$ , которые являлись бы закономерностями для нашей обучающей выборки X) ранга не более чем K (как правило берется число 3)
- доля ошибок 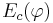$E_c ( \varphi )$ (см. предыдущий билет) для каждой из полученных конъюнкций не должна превышать $E m a x$
- доля позитивных объектов 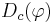$D_c ( \varphi )$ для каждой из полученных конъюнкций должна быть не меньше $D m i n$
Реализация
- перебираем все возможные конъюнкции ранга от 1 до K методом поиска в глубину:
- в процессе перебора:
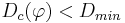
  - конъюнкция перестает наращиваться (и отбрасывается), если она выделяет слишком мало объектов своего класса, т.е. $D_c ( \varphi ) < D_{min}$
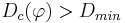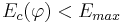
  - конъюнкция перестает наращиваться (и запоминается), если она уже удовлетворяет критериям отбора, т.е. $D_c ( \varphi ) > D_{min}$ и $E_c ( \varphi ) < E_{max}$
Достоинства алгоритма
- Короткие конъюнкции легко интерпретируются в терминах предметной области. Алгоритм способен не только классифицировать объекты, но и объяснять свои решения на языке, понятном специалистам.
- При малых K (не больше 3) алгоритм очень эффективен
- Если короткие информативные конъюнкции существуют, они обязательно будут найдены, так как алгоритм осуществляет полный перебор.
Недостатки алгоритма
- При неудачном выборе множества предикатов $B$ коротких информативных конъюнкций может просто не существовать. В то же время, увеличение числа K приводит к экспоненциальному падению эффективности.
- Алгоритм не стремится обеспечивать равномерность покрытия объектов. Это отрицательно сказывается на обобщающей способности (вероятности ошибки) алгоритма.

Пример применения данного алгоритма - motp.pdf, страница 5

[править] Тесты, представительные наборы, проблемы перебора.

Матрица эталонов $T n m i$ : Каждый столбец соответсвует определенному признаку. Каждая строка - эталонному объекту. Последовательно идущий набор строк - определяет класс.

Подмножество столбцов матрицы эталонов называется тестом, если в подтаблице, образованной данным подмножеством столбцов, все строки, относящиеся к разным классам, различны.

Тупиковый тест - минимальная подсистема признаков(столбцов), разделяющая эталонные объекты разных классов.

Пример - алгоритм Кора, файл motp.pdf 5 страница. Фактически, характеристики классов строятся при помощи тестов.

Пусть объект 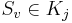$S_v \in K_j$ . Набор признаков 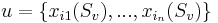$u = \{x_{i1}(S_v),..., x_{i_n}(S_v)\}$ называется $ε$ -представительским (или просто представительским), если 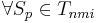$\forall S_p \in T_{nmi}$ и не лежащих в классе $K j$ система неравенств 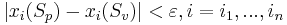$|x_{i}(S_p) - x_{i}(S_v)|< \varepsilon, i = i_1,...,i_n$ несовместна.

Существуют эффективные алгоритмы поиска тупиковых тестов. Тем не менее, задача нахождения множества всех тупиковых тестов является вычислительно сложной комбинаторной задачей и не может быть решена на современных компьютерах даже для относительно небольших таблиц обучения (сотни объектов и признаков). Поэтому при решении практических задач вычисляют и используют в процедурах голосования обычно лишь часть тупиковых тестов.

[править] Пространства объектов для АВО. Обучающие и контрольные объекты. Метрические описания объектов в АВО.

Алгоритмы вычисления оценок

Дано:

$S = \{s_i\},~~ i \in [1, m]$ -- множество объектов. обучающая выборка
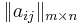$\| a_{ij} \|_{m \times n}$ -- совокупность из $m$ объектов, каждый из $n$ признаки
области определения признаков -- метрические пространства $M t$ с метриками $\rho_t:M^2_t \rightarrow \mathbb{R^+},~~ t \in [1, n]$
$K = \{K_i\}~,~~i \in [1, l]$ -- можество классов, на которые разделяются объекты
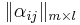$\| \alpha_{ij} \|_{m \times l}$ -- информационная матрица (таблица), с указанием того, какой из каждых $m$ объектов каким классам принадлежит

Описание класса -- список объектов из обучающей выборки, которые входят в класс, и список тех, которые не входят

Контрольная выборка -- набор из q объектов, предназначенных для определения разных параметров алгоритма:

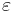$\varepsilon$ -- параметры близости
${Ω}$ -- опорные множества
$p w$ -- веса опорных множеств
$x 1, x 2$ -- коэффициентов для формулы вычисления оценок
$γ j$ -- веса обучающих объектов

Так как пространство признаков не обязательно является числовым, то имеет смысл задавать объект через меры близости к объектам обучающей выборки (метрическое описание объектов) : 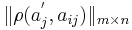$\| \rho(a^'_{j}, a_{ij}) \|_{m \times n}$ , где

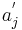$a^'_j$ -- j-тый признак описываемого объект
$a i j$ -- j-тый признак i-того объекта базовой выборки $S$

[править] Опорные множества в АВО. Функции близости. Веса объектов и признаков.

Система опорных множеств -- любое множество, элементы которого - непустые подмножества признаков {1,2...n}. При этом каждый признак должен входить хотя бы в одно множество:

$\{\Omega\}_A ~ : ~ \Omega_j = \{u_1, u_2, \dots, u_k\},~ u_k \in [1,n]$ -- совокупность опорных множеств, задающих алгоритм распознавания A
$\forall i \in [1,k] ~~ \exists j : i \in \Omega_j$ , каждый признак хотя бы в одном опорном множестве.
вместо $Ω j$ можем рассматривать характеристический вектор 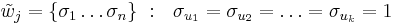$\tilde w_j = \{\sigma_1 \dots \sigma_n\}~:~~\sigma_{u_1} = \sigma_{u_2} = \dots = \sigma_{u_k} = 1$ , а остальные координаты равны нулю

Примеры опорных множеств:

совокупность всех непустых подмножеств признаков {1,2...n}. его мощность: $2 n - 1$
совокупность из всех подмножеств из k элементов. его мощность: $C^n_k$

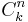
Функция близости 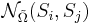$\mathcal{N}_{\tilde\Omega}(S_i, S_j)$ -- задает расстояние между проекциями объектов $S i$ и $S j$ на 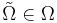$\tilde\Omega \in \Omega$ . В дальнейшем рассматриваются только такие функции 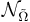$\mathcal{N}_{\tilde \Omega}$ , которые принимают значения 0 или 1 (бинарные).

Три вида функции близости:

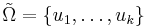Введем неотрицательные параметры $\varepsilon_i > 0 ~,~ i \in [1,n]$ . Пусть $\tilde\Omega=\{u_1, \dots, u_k\}$ . Тогда $\mathcal{N}_{\tilde\Omega}(S_i, S_j) = \begin{cases} 1,~~\rho(\alpha_{i,u_l}, \alpha_{j,u_l}) \leqslant \varepsilon_{u_l}~~\forall l \in [1,k]\\ 0,~~otherwise \end{cases}$
Введем дополнительно к п.1 параметр $ν$ такой, что функция близости будет определятся как 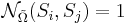$\mathcal{N}_{\tilde\Omega}(S_i, S_j) = 1$ , если не выполнено не больше, чем $ν$ описанных неравенств. при этом имеет смысл брать $0 \leqslant \nu \leqslant \left[\frac{k}{2} - 1\right]$
Вместо $ν$ определяем $ν'$ и функцию близости так, что 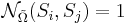$\mathcal{N}_{\tilde\Omega}(S_i,S_j) = 1$ , если из k неравенств не выполнены r, причем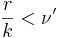 $\frac{r}{k} < \nu'$

К билету был вопрос: какие сколько возможных выборок 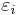$\varepsilon_i$ стоит рассматривать. Вообще говоря 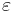$\varepsilon$ -действительно так-что континуум. Но смысл будут нести только l*m*n вариантов. где l - число признаков(колчисетво этих 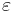$\varepsilon$ ),m - число компонент обучающей выборки, n - число компонент контрольной выборки. 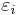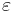Другими словами мы $\varepsilon_i$ задаем какое хотим, но обычно его задают между значениями признаков на выборке, при этом всего у нас m*n сравнений и таким образом m*n вариантов его задать(для одного $\varepsilon$ )

[править] Формулы вычисления оценок. Эвристические обоснования.

Формула вычисления оценок:

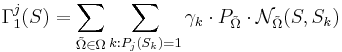$\Gamma_1^j (S) = \sum_{\tilde \Omega \in \Omega} \sum_{k : P_j(S_k) = 1} \gamma_k \cdot P_{\tilde \Omega} \cdot \mathcal{N}_{\tilde \Omega}(S, S_k)$ , где:

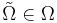$\tilde \Omega \in \Omega$ -- опорные множества
$P j (S k) = 1$ если объект $S k$ входит в класс $j$ .
$γ k$ -- вес объекта $S k$ .
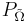$P_{\tilde \Omega}$ -- вес опорного множества.

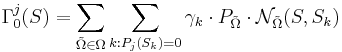$\Gamma_0^j (S) = \sum_{\tilde \Omega \in \Omega} \sum_{k : P_j(S_k) = 0} \gamma_k \cdot P_{\tilde \Omega} \cdot \mathcal{N}_{\tilde \Omega}(S, S_k)$ , где:

$P j (S k) = 0$ если объект $S k$ не входит в класс $j$ .

Итоговая формула для оценки принадлежности объекта $S$ классу $j$ :

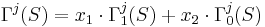$\Gamma^j(S) = x_1 \cdot \Gamma_1^j (S) + x_2 \cdot \Gamma_0^j (S)$ , где $x 1, x 2$ -- коэффициенты, которые определяют работу с соответствующими характеристиками.

[править] Задачи оптимизации АВО. Совместные подсистемы систем неравенств.

lekcii_ama_zuravlev.doc, пункт 2.4
Оптимизация АВО по метрикам

[править] Функционалы качества. Сложность моделей алгоритмов и проблема переобучения.

Функционал качества алгоритма. Пусть задана таблица контрольных объектов (множество объектов, на которых мы будет проверять качество работы нашего алгоритма распознавания). Для контрольных объектов мы должны знать, к какому классу свойств относится каждый из объектов (иначе как мы будет проверять корректность работы нашего алгоритма). Подаем контрольные объекты на вход алгоритму. Доля правильных ответов, выданных алгоритмов - это и есть функционал качества (в простейшем случае).

Обобщающая способность (generalization ability, generalization performance). Говорят, что алгоритм обучения обладает способностью к обобщению, если вероятность ошибки на тестовой выборке достаточно мала или хотя бы предсказуема, то есть не сильно отличается от ошибки на обучающей выборке. Обобщающая способность тесно связана с понятиями переобучения и недообучения.

Переобучение, переподгонка (overtraining, overfitting) — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда вероятность ошибки обученного алгоритма на объектах тестовой выборки оказывается существенно выше, чем средняя ошибка на обучающей выборке. Переобучение возникает при использовании избыточно сложных моделей.

Недообучение — нежелательное явление, возникающее при решении задач обучения по прецедентам, когда алгоритм обучения не обеспечивает достаточно малой величины средней ошибки на обучающей выборке. Недообучение возникает при использовании недостаточно сложных моделей.

[править] Общие пространства начальных и финальных информаций. Задачи синтеза корректных алгоритмов.

Диссертация Рудакова, пункт 1.1

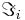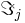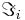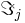В самой общей постановке задача синтеза алгоритмов преобразования информаций состоит в следующем. Имеется множество начальных информаций $\Im_i$ и множество конечных информаций $\Im_j$ . Требуется построить алгоритм реализующий отображение из $\Im_i$ в $\Im_j$ , удовлетворяющее заданной системе ограничений.

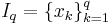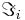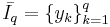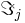Одним из частных случаев является задача обучения по прецедентам, в которой система ограничений задаётся следующим образом. Фиксируется последовательность $I_q = \{x_k\}_{k=1}^{q}$ элементов множества $\Im_i$ и последовательность $\bar{I_q} = \{y_k\}_{k=1}^{q}$ элементов множества $\Im_j$ . Искомый алгоритм $A$ должен точно или приближённо удовлетворять системе из $q$ равенств 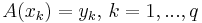$A(x_k)= y_k,\,k=1,. . .,q$ , которую мы будем сокращённо записывать как 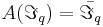$A(\Im_q) = \bar{\Im_q}$ . Ограничения такого типа называются локальными или прецедентными.

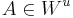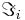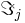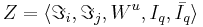Кроме того,обычно требуется, чтобы искомый алгоритм удовлетворял некоторым дополнительным ограничениям, которые в общем случае выражаются условием $A \in W^u$ где $W u$ заданное множество отображений из $\Im_i$ в $\Im_j$ . Алгоритм, удовлетворяющий локальным и дополнительным ограничениям, называют корректным. Итак, рассматриваемые задачи обучения по прецедентам определяется пятёркой $Z = \langle \Im_i, \Im_j, W^u, I_q, \bar{I_q} \rangle$ .

Различие между локальными и дополнительными ограничениями заключается в том, что первые относятся к конечному набору точек и допускают эффективную проверку, в то время как вторые накладываются на всёотображение «в целом» и не допускают эффективной проверки. В частности, это могут быть ограничения непрерывности, гладкости, монотонности, унимодальности, и т. д. На практике дополнительные ограничения учитываются на этапе построения параметрического семейства алгоритмов,а локальные при последующей настройке параметров алгоритма на заданные прецеденты

[править] Разрешимость и регулярность задач распознавания. Регулярность по Ю.И. Журавлёву

Диссертация Рудакова, пункт 1.5

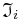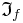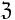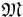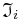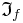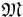Разрешимые задачи - это задачи, для которых множество допустимых отображений их $\mathfrak{I}_i$ в $\mathfrak{I}_f$ непусто, т.е. существуют семейства алгоритмов, содержащие их решения. Задача Z из множества задач $\mathfrak{Z}$ называется полной относительно семейства $\mathfrak{M}$ отображений из $\mathfrak{I}_i$ в $\mathfrak{I}_f$ , если в $\mathfrak{M}$ содержатся допустимые отображения для всех задач из класса эквивалентности, содержащего Z. 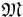Задача Z называется регулярной, если для нее существует семейство отображений $\mathfrak{M}$ , относительно которого она полна.

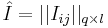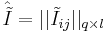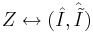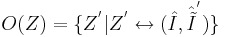Регулярность по Журавлеву: Пусть есть $q$ объектов и $l$ классов и $\hat{I}=||I_{ij}||_{q \times l}$ - матрица информации и $\hat {\tilde I} = || {\tilde I}_{ij}||_{q \times l}$ - матрица правильных ответов. Задаче Z соответствует пара матриц: $Z \leftrightarrow (\hat I , \hat{\tilde I})$ . Определение окрестности задачи по Журавлеву $O(Z)=\{Z^' |Z^' \leftrightarrow (\hat I , \hat{\tilde I}^')\}$ - т.е. это множество задач $Z'$ , получающихся всевозможным варьированием матрицы правильных ответов.

Разбиваем множество задач на классы эквивалентности. Задача называется регулярной если она разрешима и разрешимы все задачи из класса эквивалентности который она порождает.

[править] Операции над алгоритмами. Расширение моделей.

http://www.ict.edu.ru/ft/004700/VoronCanDisser.pdf

Пункт 1.2

[править] Пространства оценок. Алгоритмы как суперпозиции.

http://www.ict.edu.ru/ft/004700/VoronCanDisser.pdf

Пункт 1.2

[править] Понятие полноты моделей алгоритмов и семейств корректирующих операций.

Диссертация Рудакова 1.3 + 1.5 пункты. Диссертация Рудакова, пункт 3.5

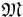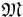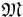Модель алгоритмов $\mathfrak{M}$ категории $Φ 0$ называется полной, если любая регулярная задача $Z$ из множества $\mathfrak{Z}_{[R]}$ полна относительно $\mathfrak{M}$ , т.е. если для любой регулярной задачи $Z$ модель алгоритмов от любой матрицы исходных информаций этой задачи приводит в множество конечных информаций. (т.е. в модели алгоритмов $\mathfrak{M}$ для каждой регулярной задачи из множества $\mathfrak{Z}_{[R]}$ содержится корректный алгоритм)

[править] Дополнительные к прецедентам ограничения. Пример: перестановочность строк и столбцов в матрицах информации.

Прецедентная (локальная) информация - описания объектов и данные о принадлежности объектов к классам. Дополнительные к прецедентным (универсальные) ограничения - формальные ограничения на вид допустимых отображений.

[править] Задачи с однородными классами

Пусть рассматривается задача, в которой имеется информация о том, что порядок, в котором анализируются классы несущественен, и кроме прецедентных данных нет сведений о различии классов. Универсальные ограничения, выражающие однородность классов, состоят в том, что отображение, реализуемое корректным алгоритмом, должно коммутировать со всеми подстановками столбцов (при любой перстановке столбцов в матрице информации точно так же должны переставляться столбцы в матрице, порожденной алгоритмом).

[править] Задачи с непересекающимися классами.

Диссертация Рудакова, пункт 2.5

[править] Класс поэлементных операций и отображений. Условия регулярности и полноты.

[править] Полнота моделей АВО.

Диссертация Рудакова, пункт 3.5

[править] Полнота полиномиальных семейств корректирующих операций.

Корректирующие операции по сути - операции над матрицами. Один из самых мощных и применяемых на практике - корректирующие полиномы некоторой степени, от матриц с Адамаровым умножением.

Основной вопрос - степень полинома, который может задать любую матрицу (и обеспечить таки образом полноту системы корректирующих операций). Было доказано, что при размерах матрицы информации $q * l$ , система из полиномов степени $q * l - 1$ - полна, $q * l - 2$ - не полна.

[править] Логарифмическая граница степени корректирующих полиномов.

Для частного случая - матрицы информации, состоящие из нулей и единиц, оценку степени корректирующих полиномов удалось улучшить. Для таких полиномов степень может быть снижена до 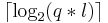$\lceil \log_2 (q * l ) \rceil$

Полезная информация к билету из Диссертации Рудакова

Определение корректирующих операций - п. 1.3 стр 27
Полнота полиномиальных семейств к.о. - п. 5.6 стр 116
Определение 0,1-полноты - определение 6.1.2 стр 119
Теорема о логарифмической границе степени корректирующих полиномов - теорема 6.1.3, стр 120

Математические основы теории прогнозирования

Материалы по курсу
Билеты (2009) | Примеры задач (2009) | Примеры задач контрольной работы (2013) | Определения из теории вероятностей

Получено с http://esyr.org/wiki/%D0%9C%D0%9E%D0%A2%D0%9F%2C_%D0%91%D0%B8%D0%BB%D0%B5%D1%82%D1%8B_%282009%29