ГОС

Материал из eSyr's wiki.

Интегралы

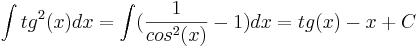
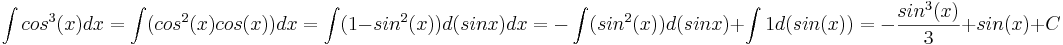
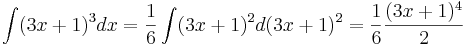
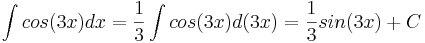
Ряды

Доказать расходимость гармонического ряда:

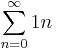
Покажем по Критерию Коши:

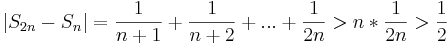
Невозможно разобрать выражение (неизвестная ошибка): Не выполняется, если взять \esp = \frac 1/4

Так как критерий Коши это необходимое и достаточное условие, то делаем вывод о расходимости ряда.

Решение линейного однородного дифференциального уравнения с постоянными коэффициентами

y^''' + 2y''' − y^' − 2y = 0 (1)

Решение этого уравнения ищется в виде y = e^λt

Подставляем этот y в уравнение (1), сокращаем на e^λt. Получаем характеристическое уравнение:

λ³ + 2 * λ² − λ − 2 = 0

Находим корни этого уравнения: λ = 1,λ = 2,λ = − 1

y₁ = e^t,

y₂ = e^2t,

y₃ = e ^{− t}

Решение уравнения (1) -- это линейная комбинация y_i,i = 1,2,3:

y = C₁y₁ + C₂y₂ + C₃y₃