Основы Кибернетики, Алгоритмы решения задач/Задачи на ДНФ
Материал из eSyr's wiki.
По заданной ФАЛ построить ее сокращенную ДНФ, ДНФ Квайна, ДНФ сумма тупиковых, все тупиковые ДНФ
Определения
Функция алгебры логики
Функция алгебры логики — функция, переводящая вектор из n-элементов множества B = {0, 1} в элемент множества B. То есть, для каждого набора нулей и единиц у функции определено значение, равное нулю или единице.
Построение сокращённой ДНФ
Определения
Буква xσ
Есть алфавит X(n) = {x1, … xn}. Буква xiσ есть xi, если σ = 1, и x̅i, если σ = 0.
Конъюнкция ранга r
Конъюнкция ранга r K = xi1σ1…xirσr, 0 ≤ r ≤ n; K = 0 при r = 0.
Элементарная конъюнкция
Элементарная конъюнкция — конъюнкция, у которой все переменные в буквах различны: xikσl ≠ xilσl при k ≠ l
Импликанта
Элементарная конъюнкция К называется импликантой f, если K ∨ f = f.
Простая импликанта
Импликанта К функции f называется простой импликантой, если при вычёркивании любой буквы K получается элементарная конъюнкция, которая не является импликантой f.
Сокращённая ДНФ
Сокращённая ДНФ — дизъюнкция всех простых импликант f
Геометрический метод (с использованием единичного куба)
- Рисуем единичный куб (для 6 и более переменных это уже затруднительно)
| Единичный куб для двух переменных | Единичный куб для трёх переменных | Единичный куб для четырёх переменных |
|---|---|---|

| 
| 
|
| Единичный куб для пяти переменных | ||

| ||
- Отмечаем все грани максимальной размерности, во всех точках которых функция равна единице
- Отмечаем все грани размерности на единицу меньше, во всех точках которых функция равна единице
- …
- Отмечаем все вершины, в которых функция равна единице
Таким образом, мы наглядно получаем максимальные грани, видим местоположение ядровых точек и т. п.
Пример
Построить сокращённую ДНФ для функции f = (0110 1111). С использованием единичного куба.
Решение. Размеченный куб представлен справа. Как видно из иллюстрации, можно выделить следующие максимальные грани:
- (1 − −) → x1
- (− 1 0) → x2x3
- (− 0 1) → x2x3
В реузльтате получим сокращённую ДНФ x1 ∨ x2x3 ∨ x2x3
Метод Блейка
Пусть у нас имеется произвольная ДНФ функции f. Определим два преобразования:
- xA ∨ xB → xA ∨ xB ∨ AB
- A ∨ AB → A
Тогда, если сначала применять к имеющейся ДНФ первое преобразование, пока это возможно, а потом — второе, то получим сокращённую ДНФ.
Пример
Построить сокращённую ДНФ по имеющейся ДНФ
x1x2x3 ∨ x1x2x3 ={применяем первое правило}= x1x2x3 ∨ x1x2x3 ∨ x1x3 ={применяем второе правило дважды}= x1x3
Метод Нельсона
Метод Нельсона использует КНФ функции f. Для построения сокращённой ДНФ по КНФ достаточно раскрыть скобки и привести подобные методом поглощения (A ∨ AB → A)
Пример
Построить сокращённую ДНФ по имеющейся КНФ f(x1,x2,x3)=(x3 ∨ x1)(x1 ∨ x2 ∨ x3)
f = x3x1 ∨ x3x2 ∨ x3x3 ∨ (x1x1) ∨ x1x2 ∨ x1x3
= x3 ∨ x3x1 ∨ x3x2 ∨ x1x3 ∨ x1x2
= x3 ∨ x1x2
Метод с использованием карт Карно
Данный метод удобен для функций от 4 переменных (его также можно использовать для функций от 3 переменных, но для них обычно используются другие методы). Он основан на нахождении блоков единиц на построенной специальном образом карте значений функции. Карта строится следующим образом: по вертикали выписываются переменные x1, x2; по горизонатли — x3, x4. Пары переменых выписываются в порядке (00), (01), (11), (10). После чего в таблицу заносятся значения функции для данных значений переменных. Рассмотрим построение карты для функции f = (f0000f0001f0010f0011 f0100f0101f0110f0111 f1000f1001f1010f1011 f1100f1101f1110f1111):
| x3 | 0 | 0 | 1 | 1 | ||
|---|---|---|---|---|---|---|
| x4 | 0 | 1 | 1 | 0 | ||
| x1 | x2 | |||||
| 0 | 0 | f0000 | f0001 | f0011 | f0010 | |
| 0 | 1 | f0100 | f0101 | f0111 | f0110 | |
| 1 | 1 | f1100 | f1101 | f1111 | f1110 | |
| 1 | 0 | f1000 | f1001 | f1011 | f1010 | |
Далее на полученной карте находим все максимально возможные блоки единиц вида 2k × 2l; k, l ∈ N, учитывая тот факт, что карта закольцована. Блоки могут пересекаться, но не должны включать друг друга. Далее для каждого блока выписывается вектор, в котором в случае, если переменная в пределах этого блока меняла значение, знак «–», если же не меняет, то её значение в пределах блока. Для позиций вектора i, в которых стоит знак σ ∈ {0, 1}? в ЭК добавляется xiσ. Дизъюнкция всех полученных ЭК и есть сокращённая ДНФ.
Пример
Найдём сокращённую ДНФ для функции f = (1010 0110 0111 1101) методом карт Карно.
На основании карты получаем следующие блоки:
- (0 0 − 0) = x1x2x4
- (0 − 1 0) = x1x3x4
- (− 0 1 0) = x2x3x4
- (− 1 0 1) = x2x3x4
- (1 1 0 −) = x1x2x3
- (1 0 1 −) = x1x2x3
- (1 − − 1) = x1x4
В результате получаем сокращённую ДНФ x1x2x4 ∨ x1x3x4 ∨ x2x3x4 ∨ x2x3x4 ∨ x1x2x3 ∨ x1x2x3 ∨ x1x4
нужно обьединить в прямоугольник единицу (с координатами [1;1]) с единицей ,у которой координаты [4;1] нужно обьединить в прямоугольник единицу (с координатами [4;1]) с единицей ,у которой координаты [4;4] прокомментировал getbraine e-mail v000du@gmail.com
Построение сокращенной ДНФ по совершенной ДНФ при помощи алгоритма Квайна
Алгоритм Квайна построения сокращенной ДНФ по совершенной ДНФ: 0) i:=1 1)Пока возможно к слагаемым ранга n-i+1 применять неполное склеивание:
xK v (not x)K = xK v (not x)K v K
2)пока возможно поглощение 3) i++; if (i<=n) goto 1
Построение ДНФ Квайна
ДНФ, которую получают путем выбрасывания всех простых импликант, соответствующих максимальным граням, которые покрываются ядром, называется ДНФ Квайна.
Алгоритм построения ДНФ Квайна:
1. получить сокращенную ДНФ;
2. найти ядровые грани;
3. удалить импликанты, покрываемые ядром.
Полученная ДНФ, является ДНФ Квайна.
Построение ДНФ ΣT (суммы тупиковых)
см ниже
Построение всех тупиковых ДНФ
Пусть мы ищем все тупиковые решения для ФАЛ f. Выпишем таблицу M(таблицу Квайна), в которой столбцам соответствуют элементы из Nf (наборы, на которых функция принимает значение 1), строкам соответствуют максимальные грани. В ячейке стоит 1, если грань, соответствующая строке содержит набор, соответствующий столбцу.
Затем выписываем КНФ функции покрытия следующим образом:
Пусть каждой строке соответствует некоторая переменая yi.
Для каждого столбца, переменные, соотвествующие строкам в которых в данном столбце стоит 1, запишем через логическое или. Функция покрытия равна произведению таких сумм для каждого столбца.
Пример
Есть функция g: Ng = {α1 = (100), α2 = (110), α3 = (010), α4 = (011), α5 = (001), α6 = (101) }.
Множество максимальных граней = {N1,…,N6}, где Ni={αi,αi+1}, причем α7=α1.
Таблица Квайна:
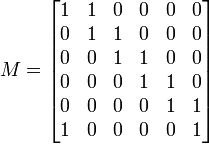
ФАЛ покрытия: F(y) = (y6 ∨ y1)(y1 ∨ y2)(y2 ∨ y3)(y3 ∨ y4)(y4 ∨ y5)(y5 ∨ y6).
Раскрывая скобки и приводя подобные, получаем:
F(y) = y1y3y5 ∨ y2y4y6 ∨ y1y2y4y5 ∨ y2y3y5y6 ∨ y1y3y4y5.
Это соответствет тупиковым покрытиям 1 = N1N3N5; 2 = N2N4N6; и т.д.
Пример
Построить все тупиковые ДНФ для ФАЛ f = (1010 0110 0111 1101).
Решение.
Сокращённая ДНФ для данной функции есть x1x2x4 ∨ x1x3x4 ∨ x2x3x4 ∨ x2x3x4 ∨ x1x2x3 ∨ x1x2x3 ∨ x1x4 (как было получено ранее). Выпишем все точки, где ЭК принимают значение, равное единице, следующим образом:
| ЭК | x1x2x4 | ∨ | x1x3x4 | ∨ | x2x3x4 | ∨ | x2x3x4 | ∨ | x1x2x3 | ∨ | x1x2x3 | ∨ | x1x4 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| αi | α1 = (0000) α2 = (0010) | α2 = (0010) α3 = (0110) | α2 = (0010) α4 = (1010) | α5 = (0101) α6 = (1101) | α7 = (1100) α6 = (1101) | α4 = (1010) α8 = (1011) | α9 = (1001) α8 = (1011) α6 = (1101) α10 = (1111) |
Построим таблицу (таблицу Квайна), у которой по строкам указаны ЭК, а по столбцам — точки, где функция принимает значение, равное единице. На пересечении ЭК и точки будет стоять значение ЭК в этой точке (фактически, входит ли данная точка в характеристическое множество данной ЭК, или нет). Для наглядности, единицы выделены.
| α1 | α2 | α3 | α4 | α5 | α6 | α7 | α8 | α9 | α10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| K1 = x1x2x4 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| K2 = x1x3x4 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| K3 = x2x3x4 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| K4 = x2x3x4 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| K5 = x1x2x3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| K6 = x1x2x3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| K7 = x1x4 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
Далее, определим ядровые точки, то есть те αi, у которых в столбце только одна единица. Таковыми являются α1, α3, α5, α7, α9, α10. Соответственно, ядровыми гранями являются те грани, которые соответствуют конъюнкциям, которым принадлежат ядровые вершины (смотрим на строки, в которых хотя бы для одного из выбранных столбцов αi стоит единица), то есть K1, K2, K4, K5, K7. Дизъюнкция этих конъюнкций есть пересечение тупиковых.
Для нахождения всех тупиковых ДНФ построим КНФ, элементарныё дизъюнкции которой будут состоять из БП, соответствующих тем конъюнкциям, в которые входит рассматриваемая точка αi (то есть, всего дизъюнкций столько же, сколько есть точек, где фугкция принимает единичное значение, причём первая дизъюнкция будет содержать те БП, которые соответствуют тем ЭК, которым принадлежит α1 (в данном примере это K1), вторая — те, которые соответствуют ЭК, которым принадлежит α2 (K1, K2, K3), и так далее):
K1 & (K1 ∨ K2 ∨ K3) & K2 & (K3 ∨ K6) & K4 & (K4 ∨ K5 ∨ K7) & K5 & (K6 ∨ K7) & K7 & K7
После раскрытия и приведения подобных получим ДНФ, состоящих из ЭК, которые будут соответствовать тупиковым ДНФ, причём БП в ЭК будут соответствовать ЭК, входящим в тупиковую ДНФ:
K1 & (K1 ∨ K2 ∨ K3) & K2 & (K3 ∨ K6) & K4 & (K4 ∨ K5 ∨ K7) & K5 & (K6 ∨ K7) & K7 & K7 = K1K2K4K5K7 & (K1 ∨ K2 ∨ K3) & (K3 ∨ K6) & (K4 ∨ K5 ∨ K7) & (K6 ∨ K7) = K1K2K4K5K3K7 ∨ K1K2K4K5K6K7
ДНФ K1K2K3K4K5K7 ∨ K1K2K4K5K6K7 соответствует тупиковым ДНФ
| K1 ∨ K2 ∨ K3 ∨ K4 ∨ K5 ∨ K7 | x1x2x4 ∨ x1x3x4 ∨ x2x3x4 ∨ x2x3x4 ∨ x1x2x3 ∨ x1x4 |
|---|---|
| K1 ∨ K2 ∨ K4 ∨ K5 ∨ K6 ∨ K7 | x1x2x4 ∨ x1x3x4 ∨ x2x3x4 ∨ x1x2x3 ∨ x1x2x3 ∨ x1x4 |




