Методы Оптимизации, Теормин

Материал из eSyr's wiki.

Перейти к: навигация, поиск

Содержание

Введение в теорию сложности

Индивидуальная и массовая задачи, кодировка задачи, алгоритм решения массовой задачи, временная сложность алгоритма.

Массовая задача Π:

  • список свободных параметров;
  • формулировка свойств, которым должно удовлетворять решение задачи.

Π есть множество индивидуальных задач 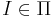I \in \Pi. Индивидуальная задача получается, если всем параметрам присвоить конкретные значения.

Пусть E - конечный алфавит, а E* - множество слов в этом алфавите. Отображение e: 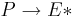P \rightarrow E* называется кодировкой задачи П.

Алгоритм A решает массовую задачу Π, если для любой индивидуальной задачи 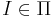I \in \Pi :

  • A применим к I, то есть останавливается за конечное число шагов
  • A дает решение I

Кодировка задачи P -- такое отобраение 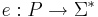e: P \rightarrow \Sigma^* , обладающее следующими свойствами:

  • Возможность однозначно декодировать, то есть у двух различных ИЗ не может быть одинаковых кодировок.
  • e,e − 1 -- полиномиально вычислимы
  • Кодировка не избыточна, то есть для любой другой кодировки e1, удовлетворяющей 1 и 2 условиям справедливо:

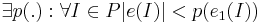
\exists p(.): \forall I \in P |e(I)| < p(e_{1}(I))

Язык массовой задачи -- это множество правильных слов, то есть слов, соответствующих ИЗ, имеющим положительный ответ(подразумевается задача распознавания): 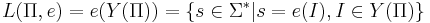L(\Pi, e) = e(Y(\Pi)) = \{s \in \Sigma^*| s = e(I), I \in Y(\Pi)\}

Язык алгоритма -- множество слов, принимаемых A, то есть таких, на которых алгоритм останавливается в состоянии qY, что соответсвует "да": 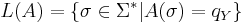L(A) = \{\sigma \in \Sigma^* | A(\sigma) = q_Y\}

Алгоритм A решает массовую задачу Π, с кодировкой e, если L(e,Π) = L(A)

tA(s) -- число шагов алгоритма A для входа 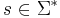s \in \Sigma^*.

Временная сложность 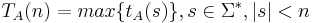T_{A}(n) = max \{t_{A}(s)\}, s \in \Sigma^*, |s| < n .

Задачи распознавания свойств. Классы P и NP.

Задача распознавания свойств -- массовая задача, предполагающая ответ "да" или "нет", в качестве своего решения.

  • D(Π) -- множество всех возможных значений параметров массовой задачи.
  • Y(Π) -- множество всех индивидуальных задач, ответом на которые является "да".

Класс полиномиально разрешимых задач (P) -- это такие задачи, временной сложность алгоритма решения которых ограниченна полиномом:

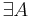  • \exists A такой, что A решает массовую задачу Π с кодировкой e
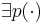  • \exists p(\cdot) -- полином такой, что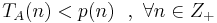 T_A(n) < p(n)~~,~\forall n \in Z_{+}

Примеры неполиномиальных задач:

  • алгоритмически неразрешимые задачи: 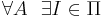\forall A ~~ \exists I \in \Pi такая, что A не применим к I, например,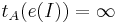 t_A(e(I)) = \infty
    • 10-я проблема Гильберта: по данному многочлену g с целыми коэффициентами выяснить, имеет ли уравнение g = 0 целочисленное решение
  • задачи, для которых длина записи выхода превышает любой наперед заданный полином от длины входа
    • найти все маршруты в задаче коммивояжёра

Класс недетерменированно полиномиальных задач (NP) -- это такие задачи, для которых существует алгоритм решения на недерменированной машине Тьюринга:

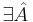  • \exists \hat{A} для НДМТ такой, что 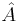\hat{A} решает массовую задачу Π с кодировкой e
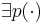  • \exists p(\cdot) -- полином такой, что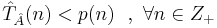 \hat{T}_{\hat{A}}(n) < p(n)~~,~\forall n \in Z_{+}

Теорема об экспоненциальной временной оценке для задач из класса NP.

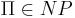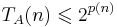Для любой \Pi \in NP существует ДМТ A, решающая ее с не более чем экспоненциальной временной сложностью: T_A(n) \leqslant 2^{p(n)} .

Класс co-NP. Пример задачи, допускающей хорошую характеризацию. Доказательство утверждения о взаимоотношении классов NPC и co-NP.

Дополнительная задача 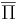\overline\Pi к массовой задаче Π -- задача, получаемая из Π путем введения альтернативного вопроса. То есть если в Π спрашиваем "верно ли x", то в 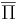\overline\Pi спрашиваем "верно ли, что \neg x"

  • D(\overline{\Pi}) = D(\Pi)
  • Y(\overline{\Pi}) = D(\Pi) \setminus Y(\Pi)

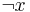Класс co-P -- 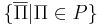\{\overline{\Pi} | \Pi \in P\}

  • co-P = P.

Класс co-NP -- 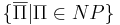\{\overline{\Pi} | \Pi \in NP\}.

  • co-NP = NP пока не удалось ни доказать, ни опровергнуть.
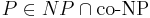
  • P \in NP \cap \text{co-NP}

Массовая задача Π допускает хорошую характеристику, если 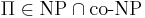\Pi \in \text{NP} \cap \text{co-NP}

  • пример такой задачи -- это задача определения простоты числа.
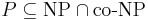
  • P \subseteq \text{NP} \cap \text{co-NP}

Массовая задача Π' с кодировкой e' полиномиально сводится к задаче Π с кодировкой e, если любая индивидуальная задача 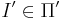I' \in \Pi' может быть сведена за полиномиальное от её длины время к некоторой задаче 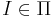I \in \Pi с сохранением ответа.

Массовая задача Π называется NP-полной (универсальной), если

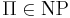
  • принадлежит классу NP: \Pi \in \text{NP}
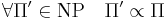
  • любая задача из NP полиномиально сводится к Π: \forall \Pi' \in \text{NP} ~~~ \Pi' \propto \Pi

Класс NPC (NP-complete) -- множество всех NP-полных задач.

Критерий NP-полноты. Д-во NP-полноты задачи ЦЛН

Д-во NP-полноты задачи 3-выполнимость. NP-трудные задачи

Взаимоотношение классов P, NP и NPC, NP и co-NP. Класс PSPACE

Гипотеза. 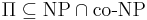\Pi \subseteq \text{NP} \cap \text{co-NP}

Гипотеза. Если для некоторой NP-полной задачи Π дополнительная к ней задача 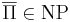\overline{\Pi} \in \text{NP}, то NP = co-NP

Класс PSPACE массовых задач -- класс алгоритмов, требующих не более, чем полиномиальной памяти.

Гипотеза. 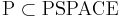\text{P} \subset \text{PSPACE}. При этом NP-полные, NP-трудные, NP-эквивалентные задачи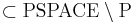 \subset \text{PSPACE} \setminus \text{P}

Псевдополиномиальные алгоритмы. Пример для задачи о рюкзаке

Псевдополиномиальный алгоритм - полиномиальный алгоритм, проявляющий экспоненциальный характер только при очень больших значениях числовых параметров.

Пусть M(I) -- некоторая функция, задающая значение числового параметра индивидуальной задачи I. Если таких параметров несколько, в качестве M(I) можно взять или максимальное, или среднее значение, а если задача вовсе не имеет числовых параметров (например, раскраска графа, шахматы и т.п.), то M(I) = 0. Алгоритм называется псевдополиномиальным, если он имеет оценку трудоемкости Tmax(I) = O(p( | I | ,M(I))), где 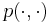p(\cdot, \cdot) -- некоторый полином от двух переменных.

Сильная NP-полнота. Теорема о связи сильной NP-полноты задачи с существованием псевдополиномиального алгоритма ее решения

Основы линейного программирования

Определение озЛП. Принцип граничных решений. Алгебраическая и битовая сложность ЛП. Результаты о сложности для задач, близких к ЛП

ЛП:

(1)Ax < = b,x = {xi},i = 1...n, существует ли 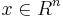x \in R^{n}, удовлетворяющий данной системе линейных неравентсв

озЛП:

найти такой 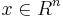x \in R^{n} -- решение (1) и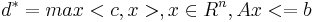 d^{*} = max<c, x>, x \in R^{n}, Ax <= b


Утверждение (принцип граничных решений). Если озЛП имеет решение, то найдется такая подматрица AI матрицы А, что любое решение системы уравнений AIx = bI реализует максимум c(x).

Алгебраическая сложность - количество арифметических операций.

Битовая сложность - количество операций с битами. Битовая сложность задач ЛП, ЛН полиномиальна. 

Вопрос о существовании алгебраически-полиномиального алгоритма для ЛП остается открытым.

Теорема о границах решений задач ЛП с целыми коэффициентами

dt(D) = max | det(D1) | , где D_1 -- квадратная подматрица D

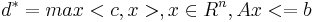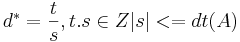
Если задача озЛп d^{*} = max<c, x>, x \in R^{n}, Ax <= b размерности (n, m) с целыми коэффициентами разрешима, что у нее существует рацональное рашение x * в шаре: || x^{*} || <= \sqrt{n} dt([A|b]) и d^{*} = \frac{t}{s}, t. s \in Z | s | <= dt(A)


Теорема о мере несовместности систем линейных неравенств с целыми коэффициентами

Определение. xε -- ε-приближенное решение системы ЛН, если < ai,xε > < = bi + ε

Теорема. Если система линейных неравенств имеет ε1 приближенное решение (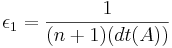\epsilon_1 = \frac{1}{(n+1)(dt(A))}), то эта система разрешима, то есть имеет точное решение.

Описание метода эллипсоидов

Лемма1.Если система Ax <= b совместна,то в шаре || x || <= \sqrt{n} dt([A|b]) найдется ее решение.

Таким образом получаем, что если система совместна, то эта лемма позволяет локализовать хотбы бы 1 из ее решений

Получено с http://esyr.org/wiki/%D0%9C%D0%B5%D1%82%D0%BE%D0%B4%D1%8B_%D0%9E%D0%BF%D1%82%D0%B8%D0%BC%D0%B8%D0%B7%D0%B0%D1%86%D0%B8%D0%B8%2C_%D0%A2%D0%B5%D0%BE%D1%80%D0%BC%D0%B8%D0%BD
Личные инструменты
Разделы