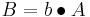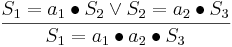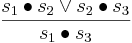ВПнМ, 01 лекция (от 08 февраля)
Материал из eSyr's wiki.
Оригинальная презентация: http://savenkov.lvk.cs.msu.su/mc/lect1.ppt
Верификация программ на моделях, Верификация моделей программ, Model checking.
В курсе матлогики, который нам очень понравился, на последней лекции рассматривали два подхода к верификации: верификация теорем и верификация моделей программ. Между двумя курсами есть различие: в курсе матлогики была внутренняя логика и математичкий формализм, этот же курс направлен на практическую сторону.
В качестве инструментального средства будем использовать программу Spin.
По курсу будет практикум, проходить он будет в 758 комнате.
Содержание |
План лекции
- Правильность программ
- Актуальность верификации
- Формальные методы
- Автоматизация
- История развития и области применения
- Обзор курса
- Практикум
Эта лекция вводная. Лектор расскажет, что такое правильность программ, почему её надо проверять строгими методами. Сделает небольшой обзор методов проверки правильности программ, расскажет, как развивалась эта область, и то, как будет устроен практикум и зачёт по этому курсу. Будет экзамен. Зачёт лектор отменил, допущены будут все.
Разработка программы
Ошибки появляются в ходе разработки программы. Существуют различные модели жизненного цикла, но можно выделить основные этапы:
- Анализ
- Проектирование, в ходе которого разрабатывается архитектура системы
- Реализация
- Тестирование
- Эксплуатация, в ходе которой внедряется система, используется
Ошибки могут появляться на всех этих этапах. В ходе анализа можно не так понять пользователя, в ходе разработки архитектуры, есть ошибки в ходе тестирования и эксплуатации.
Наибольшее количество ошибок вносится на этапах проектирования и реализации. Обнаруживаются на этапе тестирования, особенно сборочного. Выглядит всё неплохо, но цена ошибки резко возрастает в ходе эксплуатации.
Правильность программ
Что такое ошибка? Ошибка --- несоответствие требованиям. Если нет требований к программе, то нет неправильности. Программа не может быть ни правильной, ни неправильной в таком случае, она может быть забавной.
Ошибки бывают в формулировке требований и в их соблюдении.
Ошибки в формулировке: реализовано вроде всё правильно, а пользователь скажет, что здесь ошибка. Такие ошибки выявляются в ходе процесса, называемого валидация.
Все другие ошибки, которые есть, выявляются во время разработки программы. Процесс поиска этих ошибок --- процесс верификации: проверка, соответствует ли реализация спецификации. При этом считается, что спецификация правильная.
В ходе верификации/валидации нужно найти ошибки, или доказать, что их нет.
Когда средство создаётся, средств на тестирование обычно нет. Но существуют другие системы, в которых ошибок не должно быть ни при каких обстоятельствах. Это системы с повышенными требованиями к надёжности. Это системы либо с большой ценой ошибки, либо приводящие к невосполнимым потерям.
Примеры:
- Ariana-5. Июнь 1996, взрыв ракеты спустя 40 секунд после старта. Ущерб --- 500 млн., стоимость разработки --- 7 млрд., причина ошибки: преобразования 64-bit float в 16-bit int
- Patriot: округление 24-bit fixed
- Sleipner A. Причина — ошибка округления при моделировании платформы.
Соответственно, для проверки правильности систем с повышенными требованиями к надёжности выборочное тестирование не подходит, и, как сказал Дейкстра, тестирование может выявить ошибки, но не показать, что их нет.
Тестирование направлено на выявление частых ошибок. Формальные методы направлены на поиск критических ошибок. Соотвтественно, редкие безвредные ошибки никого не интересуют.
Задача верификации программ в общем случае алгоритмически неразрешима. Таким образом, применение формальных методов, несмотря на общее мнение, что там что-то доказывается, что невозможно, там приводится обоснование, что их нет.
В абсолютном большинстве встречающиеся в природе системы таковы, что их ошибочность можно доказать, и это признак хорошего дизайна. По английки это называется probably correct.
Формальные методы
ФМ — использование математического аппарата, реализованного в языках, методах и средствах спецификации и верификации программ.
- Методы формальной спецификации
- Верификация
- Доказательство теорем
- Верификация на моделях
Методы верификации
- Полное тестирование. Тестирование, в ходе которого при построении тестового набора приводится обоснование, что набор полный.
- Имитационное тестирование. Это то же тестирование, только оно помогает избежать в том случае, например, если система ещё не готова.
- Доказательство теорем
- Статический анализ
- Верификация на моделях
Тестирование
Грубо разделим эти методы на методы чёрного ящика, которые основываются на полном покрытии входных данных, и метод прозрачного ящика,который основывается на полном покрытии кода.
Плюсы:
- Проверяется та программа, которая будет использоваться
- Для проведения теста не требуется дополнительных инструментальных средств
- Удобная локализация ошибки. Средства тестирования и отладки очень хорошо позволяют найти место в коде, где она находится
Минусы:
- Не всегда есть условия для тестирования системы
- Проблема с воспроизводимостью тестов. Ошибка должна быть воспроизводима для понимания и отладки. Если речь идёт про системы взаимодействия с реальным окружением или когда она связана с историей взаимодействия, то в этих случаях ошибка может быть не воспроизводима.
Эти минусы решаются применением имитационного моделирования: имитация окружения, и т. д.
Обоснование полноты тестового покрытия:
- ЧЯ: для последовательных программ сложно перебрать все входные данные
- ЧЯ: для параллельных дополнительно возникают цепочки взаимодействия и перестановки
- ЧЯ: для динамических структур, взаимодействующих с окружением --- невозможно
- ПЯ: большой размер покрытия, растёт экспоненциально с размером
- Часто невозможно построение 100% покрытия, например, в случае наличия недостижимого кода.
- Полное покрытие не гарантирует отсутствие ошибков.
Пример: полное покрытие для ЧЯ:
- Поиск выигрышной стратегии в шашках — 1014 операций (?)
Пример невозможности построения полного покрытия для прозрачного ящика:
int x = 1;
if (x == 1) {
std::cout << "Okay" << std::endl;
} else {
std::cout << "Error" << std::endl;
}
Для этой программы нельзя построить полное покрытие — ветвь else ни при каких условиях не выполнится.
Полное тестовое покрытие — не панацея. Пусть у нас имеется функция с двумя ошибками:
int strlen(const char * p) {
int len = 0;
do {
++len;
} while (*p++);
return len;
}
Для неё можно построить покрытие "a", "bbb", но оно не выявит ни одну из ошибок.
Итоги:
- Полный перебор входных данных — невозможен
- Полнота покрытия кода не гарантирует правильности
Реактивные программы
Кроме традиционных программ, которые завершаются по окончании работы, описываются в терминах «вход/выход» и число состояний которых зависит только от входных данных и переменных, также существуют так называемые реактивные программы.
Эти программы работают в бесконечном цикле и взаимодействуют с окружением. Эти программы работают в терминах стимул/реакция. Здесь и возникает цепочка взаимодействия, которая резко увеличивает количество состояний системы, и обойти их тестированием не представляется возможным.
Реактивные программы это не пыльный ... на задворках программистких технологий, и ошибки там гораздо менее очевидны. Пример — системы с разделением ресурсов.
Системы с разделением ресурсов
- Дорожный трафик. Пример с дедлоком на перекрёстке
- Телефонные сети. Если два человека звонят друг другу одновременно, то возникает блокировка.
- ОС. Пример с дедлоком
- ...
Параллельные системы
Новый источник ошибок --- совместная работа проверенных компонентов.
Обычно считается, что программы надо строить из небольших компонент. Потом их интегрируем и всё работает. Однако, возникают ошбки на другом уровне: в 1993 году аэробус садился на мокрую полосу, нужно было включить реверс, но он включился поздно, потому что для его включения нужно, чтобы крутились колёса,были выпущены шасси и было давление на колёса, что случилось не сразу.
Дополнительную сложность вносит одновременная работа.
Доказательство теорем
Есть система, свойства, есть аксиомы и правила вывода, и с помощью последних доказываются свойства.
Пример:
Пусть у нас имеется система:
И нам необходимо проверить свойство:
-
 ?
?
то есть, выполнится ли c после a. Используя следующие правила вывода:
С помощью этих правил вывода мы можем показать, что правило выполняется.
К достоинствам относится тот факт, что можно доказывать свойства для систем с бесконечным количеством состояний. Также этот подход даёт более глубокое понимание системы, даже более глубокое, чем нужно.
Недостатки: медленная работа, требуется помощь человека, неполнота аксиом в общем случае.
Статический анализ
- Анализ текста программы без его выполнения. Можно сказать, что здесь обходим граф потока управления. В общем случае задача достижимости неразрешима, и в общем случае статический анализ представляет компромисс между возможностями и потребностями. Кроме того, удобные инженерные конструкции очень плохо поддаются статическому анализу.
Однако есть достаточно узкие области, где статический анализ хорошо применим. Рассмотрим пример:
int min(int * arr, int n) {
int m;
if (n > 0) {
m = arr[0];
} //←
int i = 0;
while (i < n) {
if (m > arr[i]) {
m = arr[i];
}
i++;
}
return m;
}
Проверим, инициализирована ли переменная m в месте, отмеченном стрелочкой. Для этого расширяем множество значениий m неинициализированным состоянием (еще можно посмотреть эту лекцию спецкурса Чернова — 83.237.57.184):
- dom(m) = Int + { ω } — возможные состояния m — множество значений Int и «пустое» состояние
- NI = { ω } — неинициализированные состояния — пустое состояние
- I = Int — инициализированные состояния — состояние из множества Int
- v = Expr → {NI, I} — возможные состояния в данной точке программы
Начальное состояние — неинициализированное. И далее вычисляем отображение для каждой точки программы.
int min(int * arr, int n) {
int m; < v = { NI } >
if (n > 0) { < v = { NI } >
m = arr[0]; < v = { I } >
} //← < v = { NI, I } > (!)
int i = 0; < v = { NI, I } >
while (i < n) { < v = { NI, I } >
if (m > arr[i]) { < v = { NI, I } >
m = arr[i]; < v = { I } >
}
i++; < v = { NI, I } >
}
return m; < v = { NI, I } >
}
Видим, что переменная инициализируется только при размере массива больше 0.
Достоинства статического моделирования: высокая скорость; ответу, если он дан, можно верить. Из минусов — узкая область применения, а также ручная настройка при изменении проверяемых свойств.
Верификация программ на моделях
Можно построить модель с конечным количеством состояний, сформулировать свойства, последовательность значений предикатов и выполнить поиск по прост. состояниям, что даст ответ на вопрос, выполняются свойства или нет. Доказывается, что либо свойства выполняются на всех состояниях модели, либо свойства не выполняются.
Что нам важно:
- программа может находится в состоянии открыта/закрыта
- Состояния меняются в двух местах
Итого 4 состояния.
Контрпример — ошибка в процессе. Нашли ошибку.
Процесс верификации состоит из 3 этапов:
- Моделирование. Строим адекватную корректную модель. Цель моделирования --- объяснить. У нас есть программа, есть инструментальное средство верификации. У него есть свой язык. Иногда это делается путём трансляции с языка написания программы на входной язык средства. Но при этом может получиться слишком сложная модель. Тогда необходима абстракция, которая упрощает модель. Модель при этом должна быть корректной и адекватной. Более детально это будет рассматриваться на следующих лекциях. Корректная модель корректно моделирует, а адекватная корректно экстраполирует свойства на систему. Поскольку мы от чего-то абстрагируемся, оставляя то, что нужно, нужно знать, что нужно; модель без задачи не имеет смысла. Но обычно здесь формулируется класс свойств, например, корректна ли программа работает с разделяемыми ресурсами. Тогда построим модель программы, которая работает с разделяемыми ресурсами, от остального абстрагируемся.
- Спецификация свойств. Это темпоральная логика плюс с некоторыми добавками, которые использует Spin. Вопрос полноты свойств здесь не затрагивается. Это вопрос валидации и мы считаем, что свойства полны.
- Верификация. Мы передаём модель и свойства в инстр. систему, нажимаем на кнопку проверить, и получаем контрпример. Дальше нужно понять, о чём контрпример говорит, анализ контрпримеров --- это прерогатива человека, который разбирается, что произошло: некорректная модель, модель не подходит для свойств, неправильная модель. Однако, если контрпример подтверждается, то мы нашли ошибку. Исправляем её и запускаем заново. Если модель конечная адекватна, то мы гарантированно получим ответ. Она позволяет выявлять редкие ошибки, которые обычно тестированием не выявляются.
Недостаток: работает только для конечных моделей. Бывают такие программы и свойства, которые нельзя проверить с помощью конечной модели. Если кто-то захочет проверить самоприменимость, то никакая верификация не поможет.
Автоматизируемость
- Автоматизированное тестирование — автоматизированное выполнение тестов, это было давно. Автоматического тестирования нет.
- Доказательство теорем — участие человека существенно
- Статический анализ полностью автомат. в данной области и для данного свойства
- Верификация - участие человека сводится к построению модели и анализу контрпримеров. Проблема --- комбинаторный взрыв.
История развития
- Флойд, 1967. Ф. предложил использовать assertions, и выдвинул гипотезу, что если у нас для некоторого ЯП описаны assertions, то, с учётом того, как влияет оно на выполнение, можно доказать, что программа корректна
- Хоар ввёл триплеты (P | S | Q) и ввёл логический вывод, и в первое время это делалось вручную.
- Первый автоматический прувер --- 1971
- Дейкстра, 1975 описал язык, который более удачно позволял доказывать корректность программ. Каждому оператору сопоставлялся guard, причём если было условие, то гарды выполнялись недетерменированно.
- Хоар, 1978 описал CSP --- взаимодействующие последовательно процессы, это позволило доказывать корректность распределенных программ
Развитие методов
- Пнуэли, 1977 --- темпоральная логика, LTL. Стало возможным описывать свойства подмножеством языка и выполнимость словами языка (?)
- Пнуэли, 1981 --- предложена логика ветвящегося времени, которая лучше подходит для тонких свойств параллельных программ
- Клар, Эмерсон, 1981 --- предложен model checking, когда представляет программу в виде автомата с конечным числом состояний, обходим достижимые состояния и проверяем свойства.
- Варди и Вольпер, 1986 -- анализ конформности в model checking, это снимает ограничение на конечность числа состояний.
В основном курсе будет уделять ся первому моделчекингу
- Хольцман, 1981. Построен верификатор Spin
Проблема комбинаторного взрыва
- Бриан, 1989. Двоичные решающие диаграммы (BDD) --- мы строим пространство состояний, и склеиваем ветви согласно ряду правил
- МакМиллан, 1993. Верификатор SMV, использующий BDD
- Хольцман, Пелед, 1994 --- верификация параллельных систем.. Довольно часто бывает так, что порядок обмена не важен, тогда можно рассмотреть один из возможных --- редукция част. порядков
- 1995. Редукция част. порядков в Spin
После этого стало возможным применять верификаторы в промышленности.
Дальнейшее развитие
Было направлено на решение задачи комбинаторного взрыва
- Кларк, 1992 --- абстракция для уменьшения модели
- Эльсаиди, 1994 --- семантическая минимизация
- Пелед, 1996 Бир, 1998 --- верификация на лету, подгрузка по мере анализа и удаление просмотренного куска дерева из памяти
- Расси, 2000 - анализ достижимости с учётом спецификации --- выбор эвристики на основании свойств
- Эмерсон и Прасад, 1994 --- симметрия
Области применения верификации на моделях
- Сетевые и криптографические протоколы
- Протоколы работы кэш-памяти
- Интегральные схемы
- Стандарты
- Встроенные системы
- Драйвера
- Вообще программы на С. Для Spin есть конвертер из C в его внутренний язык
Верификация программ на моделях
Календарь
| пт | пт | пт | пт | пт | |
Февраль
| 08 | 15 | 22 | 29 | |
Март
| 14 | 21 | 28 | ||
Апрель
| 04 | 11 | 18 |
Материалы по курсу
Список вопросов к экзамену | Примеры задач: 1 2 3 4 5 | Теормин