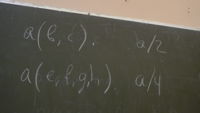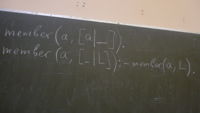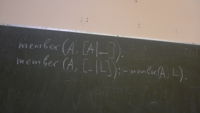Парадигмы программирования, 07 лекция (от 05 ноября)
Материал из eSyr's wiki.
- Аудиозапись: http://esyr.org/lections/audio/paradigms_2009_winter/avst_prolog.ogg, http://esyr.org/lections/audio/paradigms_2009_winter/paradigms_09_11_05.ogg
parent(john, mary). parent(john, george) parent(george, tom) sex(male,john). sex(male,mary). sex(female,geroge). sex(male,tom). brother(X, Y): sex(male, X), parent(Z, X), parent(Z, Y). ?- brother(george, A) A=mary; A=geroge; No
Таким образом, george является братом себе. Как это исправить?
brother(X, Y): sex(male, X), parent(Z, X), parent(Z, Y), X =\= Y.
В этом случае второго паразитнрого решения не будет.
Всё, конечно, хорошо, но можно заметить одну особенность: формально, они связываются конъюнкцией. Но если мы переставим X =\= Y в начало, то работать не будет, будет только для констант. Потому, что значение Y неизвестно. Поскольку нельзя перебрать бесконечность. В этом случае порядок существенен.
Получается, что есть неоторое ограничение. Совсем другео дело -- datalog, он если не может зарезолвить, то запоминает и идёт дальше. Он умеет переставлять выражения, но там поиск вширь и там нет динамических структур данных.
После того, как посмотрели пример, посмотрим более строго. Какими данными оперирует Пролог: прологовские данные, на самом деле, очень похожи на s-выр, понятно, почему: его авторы знали лисп. Пролог придуман всё для того же --- решать задачи ИИ. Ещё бы кто сказал, что это такое, есть некое интуитивное понимание.
Структуры данных, данные в языке пролог. Как и влиспе, бывают атомарные и неатомарные, сложные. Единственное, что --- в прологе неатомарных большн.
- Атомы
- Числа. Насколько помнит лектор, - не являются частью выражения.
- Идентификаторы, набранные с маленькой буквы. В прологе они называются атомами. Можно и с большой, можно и пробелы, можно вообще что угодно, только нужно взять в апострофы.: mary, john, parent, 'This is an atom, too'. В те времена, когда придумывался Пролог, ещё, видимо, не устоялись парадигмы, и небыло понимания, что имени иднтификаторов. Пролог вообще компилируемый, и одна из задач компиляции --- избавить программу от идент., введённых программистом. Но в прологе ещё одна роль атомов --- роль строк. Можно ли работать со строками иначе? Да, есть строки в дв. кавычках, но они неатомарные, это список из кодов символов. Н так работать со строками, вообще говоря, не очень эфективно. Поэтому приходится работать так.
- Структуры. Это уже дин. данные. это иден., скобка, и далее уже другие арг., в том числе структуры: triangle(point(0,0), point(1,1), point(2,0)). triangle --- функтор. Они исп. для объед. трёх разных сущностей. Треугольник --- тренарная структура, точки --- бинарные. Интересно, что есть. спец. случай функтора, который наз. точка: .(a,b) Она исп. для того же, для чего и в лиспе --- для форм. списков. В прологе они выгл. неск. иначе: [a, b, c, d] Можно ещё отделить головуот хвоста: [a,b,c|d]. [a,b,c,d] предст. как .(a, .(b, .(c, .(d, [])))) . Но здесь это не единст., а доин из многоих способов городить списки. Более того, здесь можно менять число арг. у функторов. Казалось бы, средства богаче, но ничто не мешает написать в лиспе
(triangle (point 0 0) (point 1 1) (point 2 0) )
Но это более громоздко. Зачем это сделали в Прологе? Вероятно, для удобства. Аналогично -1 --- -(1), 2+3 --- +(2, 3). Другое дело, что вычисляться оно не будет само.
Как работает пролог? Есть ключевое для пролога понятие: унификация. Это сопоставление двух термов. Под термами понимается произв. прологовское выражение. Есть два терма, их можно скормить на вход унификатору. У нас есть нек. количество перем., некоторые из них могут иметь (а могут не иметь) знач. к нач. унифик. счто явл. рез-том:
- Термы унифиц. нельзя
- Да, можно, для этого нужно, чтобы переменные приняли такие-то значения.
Переменные предст. собой контекст. После работы унифик. контекст может дополниться.
Как работает унификатор:
- Два атома унифиц., если они одинаковые. В противном случае они не унифиц.
- 1 1 => OK
- 1 2 => ∅
- mary mary => OK
- Если имеются две структуры, то первыми унифиц. функторы структуры. Если они унифиц., то идём дальше. Сравниваем арность. Если не равно, то прекращаем это дело, если арность одинаковая, то идём дальше и унфиц. аргументы. Во время унифик. могут появл. новые зн. переменных.
- Переменная. Если с одной стороны стоит переменная. Первый вариант --- она связана. Тогда унифик. происз. так, как если бы вместо перем. стояло её знач. Несвязанная перем. унифиц. с чем угодно.
Как работает пролог-решатель. Программа на прологе состоит из процедур. Предикат пролога сост. из предложений(?). Если переменных в предл. нет, то это факт, в противном случае --- не факт. Например, parent('Lord', X) --- не факт.
Кроме заголовка у процедуры есть ещё предложения. Чем объединены меджу собой: у них одинак. имя функтора и арность. Например,
a(b,c). a/2 a(e,f,g,h) a/4
Они принадл. к разным процедурам.
Как работает решательЖ Видя цель, решатель пытается найти в программе процедуру, которая соотв. именем и арносттю цели. Если не найдена такая процедура --- неуспех. Если нашли, что что делаем: мы последовательно перебираем предложения и пытаемся цель унифиц. с головой предлож. по описанному ранее алгоритму. Если не унифиц., то неуспех, если унифиц., то нач. вычисл. цели предлож, одну за другой. Интересно вот что: в каждом случае может получиться неск. решений (предложений-то несколько). Если известно, что дальше есть другие предложения, то появл. точки развилки (они, кстати, отъедают память).
Так пролог и работает. Фактически перебором.
На прологе очень хорошо решаются переборные задачи. Например: классич. задача о 8 ферзях. Понятно, что если доска n×n, то больше n досок быть не может. На прологе пишется строк в 15.
Пролог стоит изучить даже несмотря на то, что он редко где используется. Если на лиспе можно указать проекты и людей, которые на нём пишут, то для пролога Лектор это сделать не готов.
С другой стороны, есть достойные реализации --- swi prolog.
Рассмотрим пару примеров. Коли есть списки, напишем пример на списки. Является ли заданныцй элемент элементом заданного списка?
member(a, [a|_]). member(a, [_|L]) :- member(a,L).
Как это будет вычисляться? (хреново будет вычисляться, потому что a маленькая --- ManMachine)
member(A, [A|_]). member(A, [_|L]) :- member(A,L).
цель:member(1, [2, 3, 1])
member(A, [A|_]). --- унификация не удалась
member(A, [_|L]) :- member(A,L). --- унификация при A1=1, L1=[3,1]
цель: member(1, [3, 1])
member(A, [A|_]). --- унификация не удалась
member(A, [_|L]) :- member(A,L). --- унификация при A2=1, L2=[1]
цель: member(1, [1])
member(A, [A|_]). --- унификация при A3=1, _=[]
OK
OK
OK
При этом возникнет развилка, будет попытка зарезолвить member(1, []), но оно ни во что не унифицируется.
Гораздо интереснее, если мы сделаем вот так вот:
member(X, [2, 3, 1])
Здесь каждый раз будут появляться развилки. И каждый раз унификация будет проходить:
цель:member(X, [2, 3, 1])
member(A, [A|_]). --- унификация при X=2
развилка
member(A, [_|L]) :- member(A,L). --- унификация при A1=X, L1=[3,1]
цель: member(X, [3, 1])
member(A, [A|_]). --- унификация при X=3
развилка
member(A, [_|L]) :- member(A,L). --- унификация при A2=X, L2=[1]
цель: member(X, [1])
member(A, [A|_]). --- унификация при X=1
развилка
member(A, [_|L]) :- member(A,L). --- унификация при A3=X, L3=[]
цель: member(X, [])
унификация не удалась для обоих предложений.
OK
OK
OK
Введение в парадигмы программирования
01 02 03 04 05 06 07 08 09 10 11
Календарь
Сентябрь
| 24 | ||||
Октябрь
| 01 | 08 | 15 | 22 | 29 |
Ноябрь
| 05 | 12 | 19 | 26 | |
Декабрь
| 03 |
Экзамен по курсу пройдёт 10 декабря 2009 года в 18:00 в аудитории 524. | Список экзаменационных вопросов