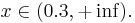МОТП, Контрольная 2013
Материал из eSyr's wiki.
Содержание |
Задача 1
Рассматривается задача классификации объектов на два класса по одному признаку. Предполагается, что значение признака x для объектов из классов K1, K2 распределено по закону Рэлея:
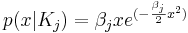
Пусть β1 = 7.3 β2 = 1.3. Требуется найти области значений признака x, соответствующие отнесению объектов в каждый из двух классов байесовским классификатором, если априорные вероятности классов равны, соответственно, 0.3 и 0.7.
Решение
По определению баесовского классификатора:
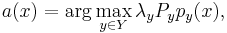
где x - классифицируемый пример, a(x) - классификатор, Y - множество классов (K1,K2), λy - цена ошибки (λ1 = λ2), Py - вероятность появления объекта класса y (априорная вероятность), py(x) - плотность распределения класса y в точке x.
Построим множество, на котором 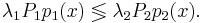 Для этого решим уравнение:
Для этого решим уравнение:
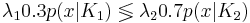
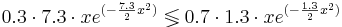
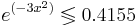
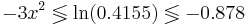
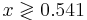
Таким образом, при x > 0.541 классификатор отнесёт объект в класс K2, при x < 0.541 - в класс K1
Задача 2
Имеется задача распознавания с 4-мя классами и одним признаком. Предполагается, что с использованием метода "Линейная машина" для каждого класса найдены следующие линейные разделяющие функции:
f1(x) = 4.8 − 2.3x
f2(x) = − 4.6 − 2.6x
f3(x) = 4.5 − 2.3x
f4(x) = 4.2 − 0.4x
Требуется изобразить на графике области, соответствующие отнесению к каждому из четырех классов.
Решение
Для нахождения требуемых областей, решим системы неравенств:
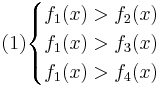
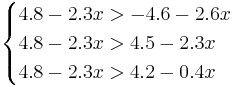
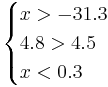
Таким образом, объект будет отнесён в класс 1 при 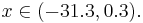
Аналогично:
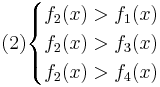
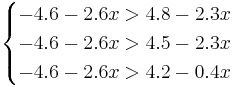
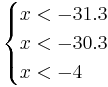
Oбъект будет отнесён в класс 2 при 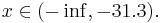
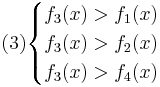
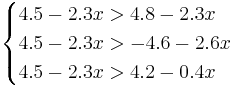
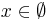 , поэтому никакой объект не будет отнесён к классу 3.
, поэтому никакой объект не будет отнесён к классу 3.
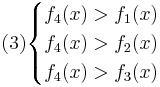
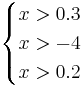
Oбъект будет отнесён в класс 4 при