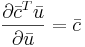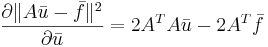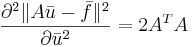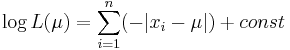МОТП, Задачи на экзамене
Материал из eSyr's wiki.
Математические основы теории прогнозирования
Материалы по курсу
Билеты (2009) | Примеры задач (2009) | Примеры задач контрольной работы (2013) | Определения из теории вероятностей
За нерешение данных задач оценка снижается на балл. — Д. П. Ветров
Содержание |
Задача 1. Вывод формул для векторного дифференцирования
Вывести (считаем все матрицы вещественными):
Решение
Формула 1
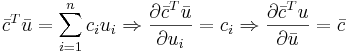
Формула 2
Далее через 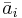 всюду обозначен столбец матрицы A с номером i.
всюду обозначен столбец матрицы A с номером i.
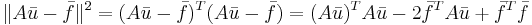
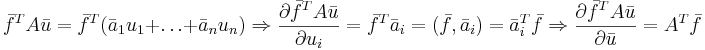
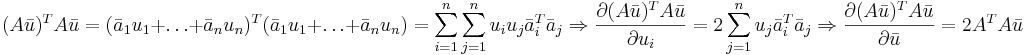
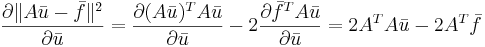
Формула 3
Далее через 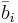 всюду обозначен столбец матрицы B с номером i.
всюду обозначен столбец матрицы B с номером i.
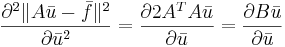
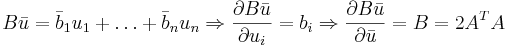
Задача 3. Метод главных компонент (PCA)
Даны р точек в двухмерном пространстве. Найти методом главных компонент первую главную компоненту.
Решение
Рассмотрим следующую задачу: p = 5, x1 = (1,1), x2 = (1,2), x3 = (3,2), x4 = (4,1), x5 = (6,4).
Находим 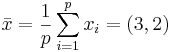 .
.
Находим 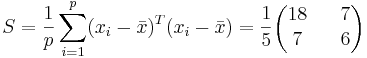
Решаем 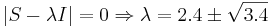 .
.
Находим собственный вектор, соответствующий 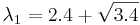 , решая
, решая 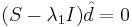 . Получаем
. Получаем 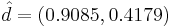 — собственный вектор, соответствующий максимальному собственному значению матрицы ковариации. Он и будет являться первой главной компонентой.
— собственный вектор, соответствующий максимальному собственному значению матрицы ковариации. Он и будет являться первой главной компонентой.
Задача 4. Метод максимального правдоподобия (ММП)
Как метко заметил Оверрайдер, будут задачки на поиск оценки максимального правдоподобия. Не сложные, но чтобы было интереснее, не с нормальным распределением. Что-нибудь типа найти оценку МП на параметр распределения Лапласа.
Решение
Плотность распределения Лапласа: 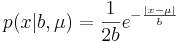 , μ - сдвиг, b - масштаб (подробнее в википедии).
, μ - сдвиг, b - масштаб (подробнее в википедии).
Вариант 1: неизвестный сдвиг, единичный масштаб
Пусть есть распределение Лапласа с неизвестным матожиданием и единичным параметром масштаба. Дана выборка, взятая из этого распределения: 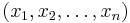 . Оценим параметр μ.
. Оценим параметр μ.
Функция распределения запишется так: 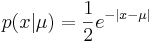
Функция правдоподобия: 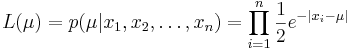
Покажем, что эта функция достигает максимума в точке 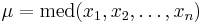 -- когда параметр равен медиане выборки.
-- когда параметр равен медиане выборки.
Упорядочим выборку по возрастанию. Пусть теперь она выглядит так: 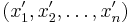 . Рассмотрим последнюю функцию на интервалах вида
. Рассмотрим последнюю функцию на интервалах вида 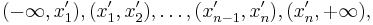 . На первом из них все функции под знаком суммы возрастают, итоговая производная равна n, на втором -- одна убывает, остальные возрастают, производная равна (n-2), и т.д. Переломный момент наступает в середине -- в одной точке перегиба (если n нечётно), или на центральном интервале производная равна 0 (если n чётно). После этого функция только убывает. Там и достигается максимум правдоподобия. Короче, нужно нарисовать график, и всё будет понятно: максимум правдоподобия достигается в точке, равной медиане выборки.
. На первом из них все функции под знаком суммы возрастают, итоговая производная равна n, на втором -- одна убывает, остальные возрастают, производная равна (n-2), и т.д. Переломный момент наступает в середине -- в одной точке перегиба (если n нечётно), или на центральном интервале производная равна 0 (если n чётно). После этого функция только убывает. Там и достигается максимум правдоподобия. Короче, нужно нарисовать график, и всё будет понятно: максимум правдоподобия достигается в точке, равной медиане выборки.
Вариант 2: нулевой сдвиг, неизвестный масштаб
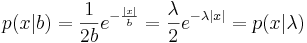
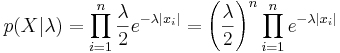
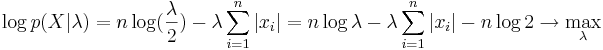
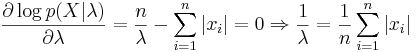
Задача 5. Линейная регрессия
Даны 3-4 точки в двухмерном пространстве - одна координата, это х, другая - t. Задача построить по ним линейную регрессию вида 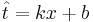 , т.е. найти коэффициенты k и b.
, т.е. найти коэффициенты k и b.
Решение
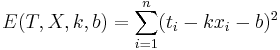
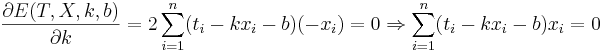
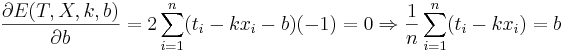
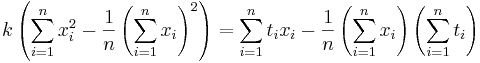
Подставляем значения для xi и ti, получаем k, затем b. Решение проверено на нескольких наборах данных в MATLAB.
Еще один вариант - посчитать напрямую (k,b) = (XTX) − 1XTY, где X - матрица, первый столбец которой составлен из xi, второй - из единиц, а Y - столбец из ti.
Задача 6. Правило множителей Лангранжа
Обязательно кому-то дам задачку на условную максимизацию квадратичной функции с линейным ограничением в виде равенства. Писанины там немного, но вот без правила множителей Лагранжа обойтись вряд ли удастся.
Решение
Пусть нам необходимо максимизировать функцию f(x,y) = − 5x2 + 2xy − 3y2 при условии x − y + 1 = 0.
Запишем функцию Лагранжа 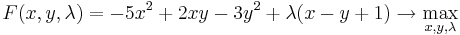 .
.
Приравняем частные производные к нулю:
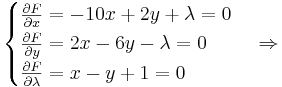
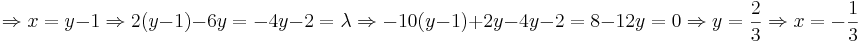 .
.
(По-моему, гораздо проще без функции Лагранжа: y = x + 1;f(x) = − 6x2 − 4x − 3;x = − b / 2a = − 4 / 12 = − 1 / 3)
Задача 11.
Решение
P(a=0) = 0.6 ; P(b=0) = 0.592 ; P(a=0 & b=0) = 0.336
Вероятности получены сложение значений вероятностей всех комбинаций, где выполняется условие. Если бы a и b были независимы, то по определению, третья вероятность была бы произведением первых двух, но это не так, поэтому a и b не независимы.
Однако a и b независимы при с=0:
P(a=0 | c=0) = P(a=0 & c=0)/P(c=0) = 0.5 (определение условной вероятности) P(b=0 | c=0) = 0.8 P(a=0 & b=0 | c=0) = P(a=0 & b=0 & c=0)/P(c=0) = 0.4 = P(a=0 | c=0) * P(b=0 | c=0)
Все остальные соотношения проверяются аналогично.
Задача 13.
all.pdf, страницы 168-169.
Оценка МП %pi - значение первой скрытой переменной, оно нам дано, поэтому вероятность P(t11 = 1) = 1,P(t12 = 1) = 0.
Оценка МП для матрицы A записана на странице 169. Содержательно эта формула означает следующее. Элемент A[i,j] - вероятность прехода из состояния i в состояние j. Оценка МП - отношение количества известных нам переходов из i в j к количеству раз, которые наблюдали систему в состоянии i. В данной задаче мы наблюдали состояние 1 100 раз, состояние 2 - 99 раз (последний раз не считается). Переход 1->2 наблюдали 25 раз, переход 1->1 - 75 раз, переход 2->1 - 24 раза, переход 2->2 - 75 раз.
Итого матрица A:
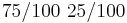
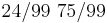
Математические основы теории прогнозирования
Материалы по курсу
Билеты (2009) | Примеры задач (2009) | Примеры задач контрольной работы (2013) | Определения из теории вероятностей