МОТП, Задачи на экзамене
Материал из eSyr's wiki.
м («Задачи на экзамене» переименована в «МОТП, Задачи на экзамене») |
(→Метод максимального правдоподобия (ММП)) |
||
| Строка 35: | Строка 35: | ||
Покажем, что эта функция достигает максимума в точке <math>\mu = \mbox{med}(x_1, x_2, \dots, x_n )</math> -- когда параметр равен медиане выборки. | Покажем, что эта функция достигает максимума в точке <math>\mu = \mbox{med}(x_1, x_2, \dots, x_n )</math> -- когда параметр равен медиане выборки. | ||
| - | Упорядочим выборку по возрастанию. Пусть теперь она выглядит так: <math>(x_1', x_2', \dots, x_n' )</math>. Рассмотрим последнюю функцию на интервалах вида <math>(-\infty, x_1'), (x_1', x_2'), \dots, (x_{n-1}', x_n'), (x_n', +\infty),</math>. На первом из них все функции под знаком суммы возрастают, итоговая производная равна ''n'', на втором -- одна убывает, остальные возрастают, производная равна (''n''-2), и т.д. Переломный | + | Упорядочим выборку по возрастанию. Пусть теперь она выглядит так: <math>(x_1', x_2', \dots, x_n' )</math>. Рассмотрим последнюю функцию на интервалах вида <math>(-\infty, x_1'), (x_1', x_2'), \dots, (x_{n-1}', x_n'), (x_n', +\infty),</math>. На первом из них все функции под знаком суммы возрастают, итоговая производная равна ''n'', на втором -- одна убывает, остальные возрастают, производная равна (''n''-2), и т.д. Переломный момент наступает в середине -- в одной точке перегиба (если ''n'' нечётно), или на центральном интервале производная равна 0 (если ''n'' чётно). После этого функция только убывает. Там и достигается максимум правдоподобия. ''Короче, нужно нарисовать график, и всё будет понятно:'' максимум правдоподобия достигается в точке, равной медиане выборки. |
==Правило множителей Лангранжа== | ==Правило множителей Лангранжа== | ||
Версия 08:23, 26 мая 2009
За нерешение данных задач оценка снижается на балл. — Д. П. Ветров
Содержание |
Метод главных компонент (PCA)
1. Даны р точек в двухмерном пространстве (буду прямо их ручкой у вас на листочке задавать). Найти методом главных компонент первую главную компоненту. Так что вспоминайте как матрицу 2х2 к главным осям приводить и ковариации считать.
Решение:
Рассмотрим следующую задачу: p = 5, x1 = (1,1), x2 = (1,2), x3 = (3,2), x4 = (4,1), x5 = (6,4).
Находим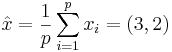 .
.
Находим 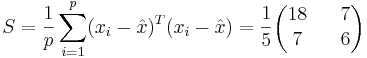
Решаем 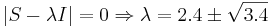
Находим собственный вектор, соответствующий 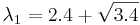 , решая
, решая 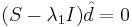 . Получаем
. Получаем 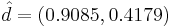 - собственный вектор, соответствующий максимальному собственному значению матрицы ковариации. Он и будет являться первой главной компонентой.
- собственный вектор, соответствующий максимальному собственному значению матрицы ковариации. Он и будет являться первой главной компонентой.
Подробные вычисления не приведены. Можете сами повторить и сверить результаты. Однако сильно не надейтесь найти ошибку, решение проверено в MATLAB.
Метод максимального правдоподобия (ММП)
2. Как метко заметил Оверрайдер, будут задачки на поиск оценки максимального правдоподобия. Не сложные, но чтобы было интереснее, не с нормальным распределением. Что-нибудь типа найти оценку МП на параметр распределения Лапласа.
Решение:
Пусть есть распределение Лапласа Laplace(μ,0) с неизвестным матожиданием и единичным параметром масштаба (о нём можно узнать из википедии). Дана выборка, взятая из этого распределения:  . Оценим параметр μ.
. Оценим параметр μ.
Функция распределения запишется так: 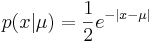
Функция правдоподобия: 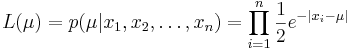
Покажем, что эта функция достигает максимума в точке 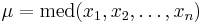 -- когда параметр равен медиане выборки.
-- когда параметр равен медиане выборки.
Упорядочим выборку по возрастанию. Пусть теперь она выглядит так: 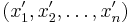 . Рассмотрим последнюю функцию на интервалах вида
. Рассмотрим последнюю функцию на интервалах вида 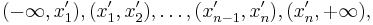 . На первом из них все функции под знаком суммы возрастают, итоговая производная равна n, на втором -- одна убывает, остальные возрастают, производная равна (n-2), и т.д. Переломный момент наступает в середине -- в одной точке перегиба (если n нечётно), или на центральном интервале производная равна 0 (если n чётно). После этого функция только убывает. Там и достигается максимум правдоподобия. Короче, нужно нарисовать график, и всё будет понятно: максимум правдоподобия достигается в точке, равной медиане выборки.
. На первом из них все функции под знаком суммы возрастают, итоговая производная равна n, на втором -- одна убывает, остальные возрастают, производная равна (n-2), и т.д. Переломный момент наступает в середине -- в одной точке перегиба (если n нечётно), или на центральном интервале производная равна 0 (если n чётно). После этого функция только убывает. Там и достигается максимум правдоподобия. Короче, нужно нарисовать график, и всё будет понятно: максимум правдоподобия достигается в точке, равной медиане выборки.
Правило множителей Лангранжа
3. Обязательно кому-то дам задачку на условную максимизацию квадратичной функции с линейным ограничением в виде равенства. Писанины там немного, но вот без правила множителей Лагранжа обойтись вряд ли удастся.
Решение:
Линейная регрессия
4. Даны 3-4 точки в двухмерном пространстве - одна координата, это х, другая - t. Задача построить по ним линейную регрессию вида 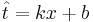 , т.е. найти коэффициенты k и b.
, т.е. найти коэффициенты k и b.
Решение:
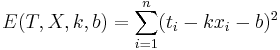
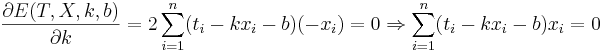
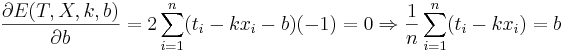
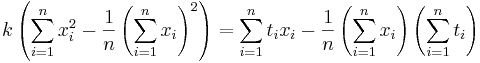
Подставляем значения для xi и ti, получаем k, затем b. Решение проверено на нескольких наборах данных в MATLAB.
Еще один вариант - посчитать напрямую (k,b) = (XTX) − 1XTY, где X - матрица, первый столбец которой составлен из xi, второй - из единиц, а Y - столбец из ti.