Основы кибернетики, Теормин
Материал из eSyr's wiki.
(Содержимое страницы заменено на «== From Ebaums Inc to MurkLoar. == We at EbaumsWorld consider you as disgrace of human race. Your faggotry level exceeded any imaginab...») |
(Отмена правки № 1280 участника 166.70.207.2 (обсуждение)) |
||
| Строка 1: | Строка 1: | ||
| - | == | + | == Представление функций с помощью дизъюнктивных нормальных форм. Тесты для таблиц == |
| - | + | ||
| - | + | === Определение <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span>, его цепи, антицепи, длины и ширины === | |
| - | + | * Отношение, обладающее свойствами рефлексивности, транзитивности, антисимметричности — ''отношение частичного порядка'' | |
| + | * Если τ — отношение частичного порядка на множестве А, то пара (А,τ) — ''частично упорядоченное множество (<span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span>)'' | ||
| + | * Для <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span> (А, τ) множество, состоящее из попарно сравнимых/несравнимых элементов а ∈ А называется ''цепью/антицепью'' | ||
| + | * Максимальная мощность цепей/антицепей <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span> называется его ''длиной/шириной'' | ||
| + | * Цепь С ⊆ А <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span> (А, τ) — ''неуплотняемая'', если С представляет собой максимальное по включению множество соответствующего типа | ||
| + | * <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span> (А, τ) длины t (|A| = t) называется ''ранжированным <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span>'', если все его неуплотняемые цепи имеют мощность t | ||
| + | |||
| + | === Определение ранжированного <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span> и утверждение о его ширине === | ||
| + | * <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span> (А,τ) длины t (|A| = t) называется ''ранжированным <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span>'', если все его неуплотняемые цепи имеют мощность t. | ||
| + | |||
| + | '''Утверждение'''. Если в ранжированном частично упорядоченном множестве (A,τ) через каждые два элемента одного и того же яруса проходит одинаковое число неуплотняемых цепей, то ширина частично упорядоченного множества (A,τ) равна максимальной мощности его ярусов. | ||
| + | |||
| + | '''Следствие'''. Ширина <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span> (B<sup>n</sup>, ≤) равна [[Изображение:Semialigned_width.png|32px]] | ||
| + | |||
| + | === Определение импликанты, простой импликанты и сокращенной <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> === | ||
| + | * <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ ''имплицирует'' <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ''g'' (или, иначе, <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ''g'' ''поглощает'' <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ) если N<sub>ƒ</sub> ⊆ N<sub>''g''</sub>, то есть импликация (ƒ → ''g'') тождественно равна 1 | ||
| + | * <span title="элементарная конъюнкция" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЭК</span>, которая имплицирует <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ, называется ''импликантой'' этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> | ||
| + | * Импликанта К <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ называется ''простой импликантой'' этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>, если она не поглощается никакой другой отличной от нее импликантой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ | ||
| + | * Дизъюнкция всех простых импликант <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ называется ее ''сокращенной'' <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> | ||
| + | |||
| + | === Тождество поглощения и определение неприводимой <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> === | ||
| + | * Тождество поглощения: ''x''<sub>1</sub> ∨ ''x''<sub>1</sub>''x''<sub>2</sub> = ''x''<sub>1</sub> | ||
| + | * <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> ''U'' вида ''U'' = ''K''<sub>1</sub> ∨ ... ∨ ''K''<sub>s</sub> называется ''неприводимой'', если соответствующее ей покрытие является неприводимым, т.е. ни одна из граней ''N<sub>K<sub>1</sub></sub>'',...,''N<sub>K<sub>s</sub></sub>'' не содержится ни в одной из других граней покрытия ''N<sub>ƒ</sub>'' = ''N<sub>K<sub>1</sub></sub>'' ∪ ... ∪ ''N<sub>K<sub>s</sub></sub>'' | ||
| + | |||
| + | === Формулировка утверждения, связанного с построением сокращенной <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> из какой-либо КНФ === | ||
| + | '''Утверждение'''. Если неприводимая <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> ''U'' получается из КНФ ''B'' <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ в результате раскрытия скобок и приведения подобных, то ''U'' — сокращенная <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ. | ||
| + | |||
| + | === Тождество обобщенного склеивания и определение нерасширяемой <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> === | ||
| + | Тождество обобщенного склеивания: ''x<sub>i</sub>K''‘ ∨ ''<span style="text-decoration:overline;">x</span><sub>i</sub>K''" = ''x<sub>i</sub>K''‘ ∨ ''<span style="text-decoration:overline;">x</span><sub>i</sub>K''" ∨ ''K''‘''K''" | ||
| + | |||
| + | * ''t''<sup>ОС</sup>: ''x''<sub>1</sub> & ''x''<sub>2</sub> ∨ <span style="border-top:solid 1px">''x''</span><sub>1</sub> & ''x''<sub>3</sub> = ''x''<sub>1</sub> & ''x''<sub>2</sub> ∨ <span style="border-top:solid 1px">''x''</span><sub>1</sub> & ''x''<sub>3</sub> ∨ ''x''<sub>2</sub> & ''x''<sub>3</sub> | ||
| + | |||
| + | === Формулировка утверждения, связанного с построением сокращенной <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> из какой-либо <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> === | ||
| + | '''Утверждение'''. Из любой <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> А <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ можно получить сокращенную <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> в результате построения последовательных строгих расширений и приведения подобных до получения неприводимой <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span>, не имеющей строгих расширений. | ||
| + | |||
| + | === Определение тупиковой, кратчайшей и минимальной <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> === | ||
| + | * <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> A, реализующая <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ называется ''тупиковой'', если ƒ ≠ A' для любой A', полученной из A удалением некоторых букв или целых <span title="элементарная конъюнкция" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЭК</span>. | ||
| + | * ''Минимальная'' (''кратчайшая'') <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> — <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span>, которая имеет наименьший ранг (длину) среди всех <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> реализующих <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ. | ||
| + | |||
| + | === Определение ядровой точки, ядровой грани и <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> Квайна === | ||
| + | * Набор ''α, α'' ∈ ''B<sup>n</sup>'', называется ''ядровой точкой'' <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ''ƒ(x<sub>1</sub>,...,x<sub>n</sub>)'', если ''α'' ∈ ''N''<sub>ƒ</sub> и ''α'' входит только в одну максимальную грань <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ. | ||
| + | * Грань ''N<sub>K</sub>'', являющаяся максимальной гранью <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ и содержащая ядровую точку ''α'', называется ''ядровой гранью''.<br> | ||
| + | * Совокупность всех различных ядровых граней <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ называется ''ядром'' <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ.<br> | ||
| + | * <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span>, получающаяся из сокращенной <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ удалением тех <span title="элементарная конъюнкция" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЭК</span> ''К'', для которых грань ''N<sub>K</sub>'' покрывается ядром <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ, но не входит в него, называется ''<span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> Квайна'' этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>. | ||
| + | |||
| + | === Определение пучка, регулярной точки и регулярной грани === | ||
| + | * Множество всех проходящих через α ( α ∈ N<sub>ƒ</sub> ) максимальных граней <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ называется ''пучком'' <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ через точку α (обозначается Π<sub>α</sub>(ƒ)). | ||
| + | * Точка α, α ∈ N<sub>ƒ</sub> называется ''регулярной точкой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ'', если существует такая точка β, что β ∈ N<sub>ƒ</sub> и Π<sub>β</sub>(f) ⊂ Π<sub>α</sub>(ƒ). | ||
| + | * Грань N<sub>K</sub> <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ называется регулярной гранью этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>, если все точки N<sub>K</sub> регулярны. | ||
| + | |||
| + | === Определение <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> сумма тупиковых и критерий вхождения в нее простых импликант === | ||
| + | * ''<span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> сумма тупиковых <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> f'' - дизъюнкция всех тех различных простых импликант этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>, которые входят хотябы в одну тупиковую <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ''f''. | ||
| + | |||
| + | '''Утверждение'''. Простая импликанта К <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> f входит в <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> ∑T тогда и только тогда, когда грань N<sub>K</sub> не является регулярной гранью этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>. | ||
| + | |||
| + | === Определение <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> пересечения тупиковых и критерий вхождения в неё простых импликант === | ||
| + | * ''<span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> пересечение тупиковых <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>'' ƒ - дизъюнкция всех тех различных простых импликант этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>, которые входят в любую тупиковую <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ. | ||
| + | |||
| + | '''Утверждение'''. <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> пересечение тупиковых <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ состоит из тех простых импликант <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ, которые соответствуют ядровым граням этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>. | ||
| + | |||
| + | === Определение линейной <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> и особенности её <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> === | ||
| + | |||
| + | * Линейная <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> — это <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ ∈ P<sub>2</sub>(n) вида ƒ(''x''<sub>1</sub>...''x''<sub>n</sub>) = α<sub>1</sub>''x''<sub>1</sub> ⊕ ... ⊕ α<sub>n</sub>''x''<sub>n</sub> ⊕ α<sub>0</sub>, где α<sub>0</sub>,...,α<sub>n</sub> — булевы константы. | ||
| + | |||
| + | '''Утверждение'''. Совершенная <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> линейной существенной функции является единственной <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> от её существенных БП. | ||
| + | |||
| + | === Необходимые и достаточные условия единственности представления <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> в виде <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> === | ||
| + | '''Утверждение'''. Совершенная <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ из P<sub>2</sub>(n) является ее единственной <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> тогда и только тогда, когда во множестве N<sub>ƒ</sub> нет соседних наборов. | ||
| + | |||
| + | === Определение монотонной <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> и её нижней единицы. Особенности простых импликант монотонной <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> === | ||
| + | * <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ (x<sub>1</sub>,...,x<sub>n</sub>) называется ''монотонной'', если ƒ(α) ≤ ƒ(β) для любых наборов α,β ∈ B<sup>n</sup> таких, что α ≤ β. | ||
| + | * Набор α ∈ B<sup>n</sup> называется ''нижней единицей'' монотонной <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ, ƒ ∈ P<sub>2</sub>(n), если α ∈ N<sub>ƒ</sub> и ƒ(β) = 0 для любого отличного от α набора β такого, что β ≤ α. | ||
| + | * Если <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ(x<sub>1</sub>,...,x<sub>n</sub>) монотонно зависит от БП x<sub>i</sub>, то ни одна из ее простых импликант не может содержать букву ¬x<sub>i</sub> | ||
| + | |||
| + | === Определение монотонной <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>, формулировка утверждения об особенностях <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> для монотонных <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> === | ||
| + | |||
| + | * <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ(''x''<sub>1</sub>...''x''<sub>n</sub>) называется ''монотонной'', если ƒ(α) ≤ ƒ(β) для любых наборов α и β куба ''B'' <sup>n</sup> таких, что α ≤ β | ||
| + | |||
| + | '''Утверждение'''. Сокращенная <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> ''U'' монотонной <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ, ƒ ∈ P<sub>2</sub>(n), является единственной тупиковой <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> этой <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> и имеет вид: ''U''(''x''<sub>1</sub>...''x''<sub>n</sub>) = ∨<sub>β∈''N''<sub>ƒ</sub><sup>+</sup></sub> ''K''<sub>β</sub><sup>+</sup>(''x''<sub>1</sub>...''x''<sub>n</sub>) | ||
| + | |||
| + | === Определение цепной и циклической <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>. Особенности <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> циклической <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>, используемые в теореме Журавлева о <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> сумма минимальных === | ||
| + | * Функция ƒ(x<sub>1</sub>,...,x<sub>n</sub>) называется ''цепной'' (''циклической'') функцией длины t, если ее сокращенная <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> с "геометрической" точки зрения представляет собой цепь (соответственно цикл) из t полседовательно соединенных ребер N<sub>1</sub>, N<sub>2</sub>, ..., N<sub>t</sub> куба B<sup>n</sup>. | ||
| + | |||
| + | * Цепная <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ нечетной длины t = 2k - 1 ≥ 3 имеет единственную минимальную <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span>, которая совпадает с ее <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> ΣM и соответствует покрытию N<sub>1</sub> ∪ N<sub>3</sub> ∪ ... ∪ N<sub>t</sub> | ||
| + | |||
| + | === Формулировка теоремы Журавлева о <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> сумма минимальных === | ||
| + | '''Утверждение (теорема Журавлева)'''. При любом n ∈ Ν, n ≥ 3, в P<sub>2</sub>(n) существуют <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ƒ' и ƒ", имеющие общую простую импликанту К, которая входит в <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> ∑M одной, но не входит в <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> ∑M другой из этих <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> и для которой S<sub>n-3</sub>(N<sub>K</sub>,ƒ') = S<sub>n-3</sub>(N<sub>K</sub>,ƒ"). | ||
| + | |||
| + | === Определение <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> покрытия матрицы и ее свойства, утверждение о КНФ для <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> покрытия === | ||
| + | * Пусть N = {α<sub>1</sub>,...α<sub>s</sub>,} - конечное множество, а П = (N<sub>1</sub>,...,N<sub>p</sub>) - система его подмножеств, образующих покрытие множества N. Сопоставим паре (N,П) матрицу M ∈ B<sup>p,s</sup>, для которой M<nowiki><i,j></nowiki> = 1 ⇔ α<sub>j</sub> ∈ N<sub>i</sub>. Будем говорить, что i-я строка матрицы М ''покрывает'' ее j-й столбец, если M<nowiki><i,j></nowiki> = 1 и что система строк с номерами из I, I ⊆ [1,p], образует ''покрытие матрицы М'', если каждый ее столбец покрывается хотябы одной строкой с номером из I, то есть система подмножеств {N<sub>i</sub>}<sub>i ∈ I</sub> задает покрытие множества N. | ||
| + | * Пусть M ∈ B<sup>p,s</sup> - матрица без нулевых столбцов. Сопоставим i-й строке матрицы М БП y<sub>i</sub>, а каждому набору β ∈ B<sup>p</sup> значений этих переменных y = (y<sub>1</sub>,...,y<sub>p</sub>) - множество строк матрицы М с намерами из множества I = I(β) ⊆ [1,p], где i ∈ I(β) ⇔ β<nowiki><i></nowiki> = 1. ФАЛ F(y), для которой F(β) = 1 ⇔ система строк матрицы М с номерами из I(β) образует ее покрытие, будем называть ''функцией покрытия'' матрицы М. | ||
| + | '''Свойства ФАЛ покрытия матрицы'''<br> | ||
| + | * монотонность | ||
| + | * ее "нижние единицы" соответствуют тупиковым покрытиям | ||
| + | '''Утверждение.''' Функция покрытия F(y<sub>1</sub>,...,y<sub>p</sub>) матрицы M ∈ B<sup>p,s</sup> без нулевых столбцов задается КНФ вида: [[Изображение:Func pokr.jpg]] (*)<br> | ||
| + | '''Следствие.''' В результате раскрытия скобок и приведения подобных из КНФ (*) можно получить сокращенную ДНФ ФАЛ F(y), простые импликанты которой взаимно однозначно соответствуют тупиковым покрытиям матрицы М. | ||
| + | |||
| + | === Градиентный алгоритм покрытия матрицы и утверждение о длине градиентного покрытия === | ||
| + | |||
| + | * Градиентный алгоритм: На каждом шаге алгоритма в матрице выбирается и включается в покрытие такая строка, которая покрывает наибольшее число ещё не покрытых столбцов (если таких строк несколько, из них выбирается строка с наименьшим номером). Алгоритм заканчивается свою работу после того шага, на котором получилось покрытие. | ||
| + | |||
| + | '''Утверждение'''. Пусть для действительного γ, 0 < γ ≤ 1, в каждом столбце матрицы ''M'', ''M'' ∈ ''B''<sup>p,s</sup>, имеется не меньше чем γ•''p'' единиц. Тогда покрытие матрицы ''M'', получаемое с помощью градиентного алгоритма, имеет длину не больше, чем [[Изображение:OcenkaProtikaniya.jpg]], где ln<sup>+</sup>x = ln x, если x ≥ 1 и ln<sup>+</sup>x = 0, если 0 < x ≤ 1. | ||
| + | |||
| + | === Определение протыкающего множества для граней единичного куба и верхняя оценка его мощности. === | ||
| + | * Пусть N = {α<sub>1</sub>,...α<sub>s</sub>,} - конечное множество, а П = (N<sub>1</sub>,...,N<sub>p</sub>) - система его подмножеств. Множество, протыкающее систему П - такое подмножество множества N,в котором ∀ i ∈ [1,p] имеется хотябы один элемент из N<sub>i</sub>. | ||
| + | '''Утверждение.''' При любых натуральных n и m, m ≤ n, в кубе B<sup>n</sup> всегда найдется множество мощности не более, чем n×2<sup>m</sup>, протыкающее все грани ранга m. | ||
| + | |||
| + | === Определение функции Шеннона R(n) для ранга <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> и ее значение. === | ||
| + | |||
| + | *R(n) = max<sub>ƒ∈P<sub>2</sub>(n)</sub> R(ƒ); | ||
| + | *R(n) = n × 2<sup>n − 1</sup> | ||
| + | |||
| + | === Определение функции Шеннона λ(n) для длины <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> и ее значение. === | ||
| + | *λ(n) = max<sub>ƒ∈P<sub>2</sub>(n)</sub> λ(ƒ); | ||
| + | *λ(n) = 2<sup>n − 1</sup> | ||
| + | |||
| + | === Определение длины <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> ''λ(ƒ)'' для <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ''ƒ'' и ее оценки для почти всех <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ''ƒ'' от ''n'' переменных === | ||
| + | * ''λ(ƒ)'' = min<sub>ДНФ U, реализующим f</sub> ''λ''(U) | ||
| + | * Для почти всех ФАЛ из P<sub>2</sub>(n) ''λ(ƒ)''<~ (3/4)*2<sup>n − 1</sup> | ||
| + | |||
| + | === Определение ранга <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span> R(f) для <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ''ƒ'' и ее оценки для почти всех <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> ''ƒ'' от ''n'' переменных === | ||
| + | * R(f) = min<sub>ДНФ U, реализующим f</sub> R(U) | ||
| + | * Для почти всех ФАЛ из P<sub>2</sub>(n) R(f)<~ (3/4)*n*2<sup>n − 1</sup> | ||
| + | |||
| + | === Определение проверяющего теста матрицы и его <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span>, утверждение и КНФ для <span title="функция алгебры логики" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ФАЛ</span> проверяющего теста === | ||
| + | Пусть есть схема Σ<sub>1</sub>, которая реализует ФАЛ ''f''<sub>1</sub>. Пусть есть источник помех И. Под действием источника И схема Σ может переходить в одно из неисправных состояний Σ<sub>2</sub>, …, Σ<sub>''s''</sub>, каждое из которых реализует ФАЛ ''f''<sub>''i''</sub>, ''i'' = <span style="border-top:solid 1px">2, s</span>. | ||
| + | |||
| + | Пусть (Σ, И) — модель ненадёжной схемы Σ с возможными состояниями Σ<sub>1</sub>, …, Σ<sub>''s''</sub>, в которых реализуются ФАЛ ''f''<sub>1</sub>, …, ''f''<sub>''s''</sub>, определённые на множестве наборов ''A'' = {α<sub>1</sub>, …, α<sub>''p''</sub>} ⊆ ''B''<sup>''n''</sup>. Рассмотрим матрицу ''M'' ∈ ''B''<sup>''p'', ''s''</sup>, ''M''[i, j] = ''f''<sub>''j''</sub>(α<sub>''i''</sub>). Множество строк матрицы ''M'' с номерами из ''T'' ⊆ [1, p] называется проверяющим тестом матрицы ''M'', если для ∀''j'' ∈ <span style="border-top:solid 1px">1, s</span>, ∃''t'' ∈ ''T'' такое, что ''M''[''t'', 1] ≠ M[''t'', ''j'']. | ||
| + | |||
| + | '''Утверждение'''. Функция проверяющего теста ''f''(''y''<sub>1</sub>, …, ''y''<sub>''p''</sub>) для отделимой по столбцам матрицы ''M'' ∈ ''B''<sup>''p'', ''s''</sup> может быть задана с помощью КНФ | ||
| + | <center>[[Изображение:Check text.png|400px]]</center> | ||
| + | где '''N''' = {(1, j) | j ∈ <span style="border-top:solid 1px">1, s</span>} | ||
| + | |||
| + | === Утверждение об оценке длины диагностического теста для произвольной таблицы с заданным числом столбцов === | ||
| + | '''Утверждение'''. Длина любого тупикового диагностического теста для отделимой по столбцам матрицы из множества ''B''<sup>p,s</sup> заключена в пределах от ⌈log s⌉ до (s − 1) | ||
| + | |||
| + | === !!! Описание <span title="частично упорядоченное множество" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ЧУМ</span>, антицепями которого являются тупиковые <span title="дизъюнктивная нормальная форма" style="text-decoration:none; border-bottom:1px dotted #C0C0C0;">ДНФ</span>. === | ||
| + | Ранжированное множество длины (n+1) всех граней n-мерного единичного куба с отношением вложения. (не точно, стр. 63) | ||
| + | |||
| + | == Основные классы дискретных управляющих систем. Структурные представления и эквивалентные преобразования схем, оценка их числа == | ||
| + | |||
| + | === Индуктивное определение формулы и реализуемой ею ФАЛ === | ||
| + | Любая переменная x<sub>j</sub> из ''X'' считается ''формулой глубины 0'' над множеством Б, которая реализует функцию x<sub>j</sub>. Если φ(x<sub>1</sub>,...,x<sub>k</sub>) ∈ Б и для каждого i, | ||
| + | i ∈ [1,k], определена формула ''F''<sub>i</sub> глубины q<sub>i</sub> над множеством Б, которая реализует функцию ƒ<sub>i</sub> из P<sub>A</sub>, то запись ''F'' вида | ||
| + | |||
| + | ''F'' = φ(''F''<sub>1</sub>,...,''F''<sub>k</sub>) | ||
| + | |||
| + | является ''формулой глубины q'' = max{q<sub>1</sub>,...,q<sub>k</sub>} + 1 над Б, которая реализует функцию ƒ вида ƒ = φ(ƒ<sub>1</sub>,...,ƒ<sub>k</sub>). | ||
| + | |||
| + | === Индуктивное определение π-схемы и нахождение реализуемой ею ФАЛ === | ||
| + | Простейшей π-схемой считается любая (1,1)-КС, которая состоит из одного контакта, соединяющего полюса. Если π-схемы ∑<sub>1</sub> и ∑<sub>2</sub> уже определены, то (1,1)-КС ∑<sub>1</sub>(∑<sub>2</sub>), которая получается в результате их последовательного (параллельного) соединения тоже является π-схемой. | ||
| + | |||
| + | === Определение разделительной по входам (выходам) КС и формулировка леммы Шеннона === | ||
| + | КС разделительна по входам (выходам), если ФАЛ проводимости для ∀ различных входов (выходов) ≡ 0. | ||
| + | |||
| + | '''Лемма Шеннона''': Пусть Σ = Σ''(Σ') - результат стыковки ⇒ F ≥ F' × F''. F = F' × F'', если Σ'' разделительна по входам, или Σ' разделительна по выходам. | ||
| + | |||
| + | === Определение подсхемы Σ' КС ∑ с указанием особенностей, связанных с объявлением вершин Σ' её полюсами. Основное тождество t<sub>4</sub> (введение фиктивной переменной) и вспомогательное тождество t<sub>11</sub> (лемма о звезде); обобщенные тождества t<sub>4</sub><sup>(n)</sup> и t<sub>11</sub><sup>(n)</sup> === | ||
| + | Определение подсхемы Σ' КС Σ:<br> | ||
| + | Σ' — подсхема схемы Σ ⇔<br> | ||
| + | # V(Σ') ⊆ V(Σ) | ||
| + | # E(Σ') ⊆ E(Σ) | ||
| + | # | ||
| + | #* ∀ полюс Σ, вошедший в Σ' — полюс Σ' | ||
| + | #* ∀ вершина Σ', инцидентная контакту Σ\Σ' - полюс Σ' | ||
| + | #* ∀ другая вершина м. б. полюсом Σ'.<br> | ||
| + | |||
| + | {| | ||
| + | !t<sub>4</sub> | ||
| + | |[[Изображение:Contact scheme t4.png|188px]] | ||
| + | |- | ||
| + | !t<sub>11</sub> | ||
| + | |[[Изображение:Contact scheme t11.png|199px]] | ||
| + | |} | ||
| + | |||
| + | === Канонический вид КС от БП x<sub>1</sub>,...,x<sub>n</sub> и формулировка утверждения о приведении КС от БП x<sub>1</sub>,...,x<sub>n</sub> к каноническому виду с помощью основных тождеств. === | ||
| + | ∑^ <i>/*здесь и далее крышка пишется над сигмой*/</i> - схема канонического вида ⇔ | ||
| + | 1) ∀ контакт ∑^ лежит на стандартной цепи порядка n, явл. подсхемой ∑^ с полюсами в конечных вершинах цепи. | ||
| + | 2) ∀ внутренняя вершина ∑^ - внутренняя вершина стандартной цепи | ||
| + | 3) в ∑^ отсутствуют висячие циклы и || стандартные цепи | ||
| + | 4) в ∑^ нет существенных транзитивных проводимостей | ||
| + | <i>/*вопрос +-, комментарий лектора: отсутствует утверждение о переходе к КВ*/</i> | ||
| + | |||
| + | ∑^ получается из ∑ удалением ∑' (подсхемы) и заменой ∑' на ∑' ' с соотв. присоединением полюсов, эквив. ∑ (принцип эквивалентной замены). | ||
| + | |||
| + | === Определение величины ||''U''<sup>c</sup>(''L'', ''n'')|| и её верхняя оценка === | ||
| + | * ''U''<sup>c</sup>(''L'', ''n'') — множество приведенных СФЭ Σ = Σ(''x''<sub>1</sub>, …, ''x''<sub>n</sub>; z<sub>1</sub>) над базисом Б<sub>0</sub>, для которых ''L''(Σ) ≤ ''L''. | ||
| + | * ||''U''<sup>c</sup>(''L'', ''n'')|| — число попарно неэквивалентных схем в ''U''<sup>c</sup>(''L'', ''n'') | ||
| + | |||
| + | '''Утверждение.''' Для любых натуральных ''n'' и ''L'' выполняется неравенство: ||''U''<sup>c</sup>(''L'', ''n'')|| ≤ (8(''L'' + ''n''))<sup>''L'' + 1</sup>. | ||
| + | |||
| + | === Определение тождества для формул и его подстановки === | ||
| + | Подстановка - вместо переменных функции F(x<sub>1</sub>, ... , x<sub>n</sub>) подставляем функции: F(F<sub>1</sub>, ... ,F<sub>n</sub>)<br> | ||
| + | Тождество - t^: F(x)' = F(x)'' (1)<br> | ||
| + | Если к правой и левой частям (1) применить подстановку, то получим тождество: | ||
| + | <center>t^ : F^' = F^'' /*здесь и далее ^ стоит над буквой ей предшествующей.*/</center> | ||
| + | где F^' = F^'(F<sub>1</sub>, ... ,F<sub>n</sub>) и F^'' = F^''(F<sub>1</sub>, ... ,F<sub>n</sub>), которое называется подстановкой для тождества t. | ||
| + | |||
| + | === Минимальный набор тождеств, входящих в расширенную основную систему, с помощью которого можно любую формулу преобразовать в формулу с поднятыми отрицаниями === | ||
| + | В расширенную основную систему входят следующие тождества: | ||
| + | r~<sup>осн</sup> = {r<sup>M</sup>, r<sup>A</sup>, r<sup>К</sup>, r<sup>ОП</sup>, r<sup>D</sup>, r<sup>ПК</sup>, t<sup>П</sup>} /* как обычно, ~ стоит над r */ | ||
| + | * r<sup>A</sup> = {t<sup>A</sup><sub>&</sub>,t<sup>A</sup><sub>∨</sub>} | ||
| + | * r<sup>K</sup> = {t<sup>K</sup><sub>&</sub>,t<sup>K</sup><sub>∨</sub>} | ||
| + | * r<sup>ОП</sup> = {t<sup>ОП</sup><sub>&</sub>,t<sup>ОП</sup><sub>∨</sub>} | ||
| + | * r<sup>D</sup> = {t<sup>D</sup><sub>&</sub>,t<sup>D</sup><sub>∨</sub>} | ||
| + | * r<sup>ПК</sup> = {t<sup>ПК</sup><sub>0, &</sub>, t<sup>ПК</sup><sub>0, ∨</sub>, t<sup>ПК</sup><sub>1, &</sub>, t<sup>ПК</sup><sub>1, ∨</sub>} | ||
| + | |||
| + | все тождества описаны [[Основы Кибернетики, Алгоритмы решения задач/Задачи на эквивалентные преобразования и структурное моделирование#Для формул|тут]]. | ||
| + | |||
| + | === !!! Определение КС от БП ''x<sub>1</sub>'',...,''x<sub>n</sub>'' как помеченного графа и ФАЛ проводимости между её вершинами === | ||
| + | |||
| + | (параграф 6 главы 2) | ||
| + | |||
| + | === Формулировка утверждения о связи между π-схемами и формулами с поднятыми отрицаниями === | ||
| + | Любой π-схеме можно сопоставить эквивалентную ей формулу ''F'' из U<sup>Ф</sup> с поднятыми отрицаниями такую, что R(''F'') = L(Σ) и обратно. | ||
| + | |||
| + | === !!! Определение эквивалентности КС Σ', Σ" и соответствующего тождества. Основное тождество ''t<sub>2</sub>'' (перестановка контактов в цепочке) и вспомогательное тождество ''t<sub>8</sub>'' ("расклейка" двух цепочек длины 2 с общим контактом); обобщенные тождества ''t<sub>2</sub><sup>(n)</sup>'' и ''t<sub>8</sub><sup>(n)</sup>'' === | ||
| + | (параграф 7 главы 2, в самом начале) | ||
| + | |||
| + | === !!! Определение суммарного цикломатического числа КС от БП ''x<sub>1</sub>'',...,''x<sub>n</sub>'' и формулировка утверждения о его изменениях при применении основных тождеств === | ||
| + | (глава 2, стр 72) | ||
| + | |||
| + | === Определение структуры CФЭ как графа специального вида и изоморфных СФЭ === | ||
| + | |||
| + | Под "абстрактной" схемой понимается сеть, часть пометок которой составляют входные переменные и в | ||
| + | каждой вершине которой реализуется функция (столбец из функций) от этих переменных. | ||
| + | При этом считается, что сама схема реализует систему (матрицу), состоящую из | ||
| + | функций (соответственно столбцов функций), реализованных на её выходах. В качестве | ||
| + | выходных пометок схемы используются, как правило, специальные выходные переменные, | ||
| + | а схема Sigma с входными переменными (входами) x<sub>1</sub>,..x<sub>n</sub> и выходными переменными | ||
| + | z<sub>1</sub>,..z<sub>m</sub> записывается в виде Sigma=Sigma(x<sub>1</sub>,..x<sub>n</sub>; z<sub>1</sub>,..z<sub>n</sub>). | ||
| + | |||
| + | Две СФЭ считаются изоморфными, если они изоморфны как помеченные графы, и эквивалентными, | ||
| + | если они реализуют равные системы ФАЛ. | ||
| + | |||
| + | === Определение ранга, сложности и глубины формулы, утверждение о соотношениях между ними === | ||
| + | |||
| + | * ''R''(''F'') — ранг формулы ''F'' — число листьев, связанного с ней дерева | ||
| + | * ''L''(''F'') — сложность формулы ''F'' — число остальных вершин, связанного с ней дерева (не листьев) | ||
| + | * ''D''(''F'') — глубина формулы ''F'' — глубина корня, связанного с ней дерева | ||
| + | * ''R''(''F'') ≤ ''L''(''F'') + 1 ≤ 2<sup>''D''(''F'')</sup> | ||
| + | |||
| + | === !!! Понятие подформулы и применение тождества к формуле === | ||
| + | |||
| + | === Минимальный набор тождеств, входящих в расширенную основную систему, с помощью которого формулу с поднятыми отрицаниями можно преобразовать в формулу со следующим порядком применения базисных функций: ¬, &, ∨ === | ||
| + | |||
| + | * Дистрибутивность ''t''<sub>&, ∨</sub><sup>D</sup>: ''x''<sub>1</sub> & (''x''<sub>2</sub> ∨ ''x''<sub>3</sub>) = (''x''<sub>1</sub> & ''x''<sub>2</sub>) ∨ (''x''<sub>1</sub> & ''x''<sub>3</sub>) | ||
| + | * Коммутативность коньюнкции ''t''<sub>&</sub><sup>К</sup>: ''x''<sub>1</sub> & ''x''<sub>2</sub> = ''x''<sub>2</sub> & ''x''<sub>1</sub> | ||
| + | |||
| + | === !!! Определение матрицы ФАЛ, реализуемой КС с ''p'' входами и ''q'' выходами, определение и свойства матрицы, реализемой КС с ''m'' неразделенными полюсами === | ||
| + | |||
| + | Глава 2, стр. 57-58 | ||
| + | |||
| + | === Определение величины ''||U<sup>π</sup>(L,n)||'' и ее верхняя оценка === | ||
| + | |||
| + | * ||U<sup>π</sup>(L,n)|| - число попарно не эквивалентных приведенных π-схем от БП x<sub>1</sub>,...,x<sub>n</sub> сложности ≤ ''L'' | ||
| + | |||
| + | * ||U<sup>π</sup>(L,n)|| ≤ (16n)<sup>L</sup> | ||
| + | |||
| + | === !!! Определение подстановки тождества для КС, связанной с управляющими БП, и ее применение к КС. Основное тождество ''t<sub>3</sub>'' (цепь из противоположных контактов) и вспомогательные тождество ''t<sub>10</sub>'' (замыкание по транзитивности); обобщенные тождества ''t<sub>3</sub><sup>(n)</sup>'' и ''t<sub>10</sub><sup>(n)</sup>'' === | ||
| + | |||
| + | === !!! Примеры моделирования основных тождеств для формул в классе СФЭ, примеры тождеств ветвления и снятия для ФЭ и входов СФЭ. Формулировка утверждения о переходе от КПСТ для ЭП формул к КПСТ для ЭП СФЭ === | ||
| + | |||
| + | == Синтез, сложность и надежность управляющих систем == | ||
| + | |||
| + | === !!! Определение сложности ''L<sup>C</sup>(F)'' системы ФАЛ ''F = (ƒ<sub>1</sub>,...,ƒ<sub>m</sub>)'' и ее тривиальная нижняя оценка для некоторых систем ФАЛ === | ||
| + | |||
| + | === Определение функции Шеннона ''L<sup>C</sup>(n)'' и ее верхние оценки, получаемые методом Шеннона и методом О. Б. Лупанова === | ||
| + | |||
| + | * ''L<sup>C</sup>(n)'' = max<sub>ƒ∈P<sub>2</sub>(n)</sub>''L<sup>C</sup>(ƒ)'' | ||
| + | * Метод Шеннона: ''L<sup>C</sup>(n)'' <∼ 8•2<sup>n</sup>/n | ||
| + | * Метод Лупанова: ''L<sup>C</sup>(n)'' ≤ (2<sup>n</sup>/n)•(1 + (5log''n'' + ''O''(1))/n) | ||
| + | |||
| + | === Нижняя оценка функции Шеннона ''L<sup>π</sup>(n)'' и то мощностное соотношение, из которого она выводится === | ||
| + | * ''L<sup>π</sup>(n)'' ≥ ''2<sup>n</sup>'' / ''log<sub>2</sub>n '' (Асимптотически больше) | ||
| + | * ''||U<sup>π</sup>(L,n)|''| ≤ ''(16n)<sup>L</sup>'' | ||
| + | |||
| + | === Определение мультиплексорной ФАЛ ''M<sub>n</sub>'' порядка ''n'', утверждение о сложности ее реализации в классах ''π''-схем и формул === | ||
| + | |||
| + | Функция вида | ||
| + | µ<sub>n</sub>(x<sub>1</sub>,..x<sub>n</sub>,y<sub>0</sub>,..y<sub>2<sup>n</sup>-1</sub>) = U <sub>(a=(a<sub>1</sub>,..a<sub>n</sub>))</sub> x<sub>1</sub><sup>a<sub>1</sub></sup>...x<sub>n</sub><sup>a<sub>n</sub></sup>y<sub>v(a)</sub> | ||
| + | называется мультиплексорной функцией (мультиплексором) порядка n, а переменные | ||
| + | x=(x<sub>1</sub>,..x<sub>n</sub>) называются адресными, | ||
| + | y=(y<sub>0</sub>,..y<sub>2<sup>n</sup>-1</sub>) - информационными БП мультиплексора µ<sub>n</sub>. | ||
| + | |||
| + | L<sup>п</sup>(µ<sub>n</sub>) <= 3*2<sup>n</sup>-2, | ||
| + | L<sup>Ф</sup>(µ<sub>n</sub>) <= 2<sup>n+2</sup>-3; | ||
| + | |||
| + | === !!! Определение сложности ''L<sup>K</sup>(ƒ)'' ФАЛ ''ƒ(x<sub>1</sub>...x<sub>n</sub>)'' в классе КС и её тривиальные нижние оценки для ФАЛ ''ƒ'', существенно зависящей от всех своих переменных (с учетом характера этой зависимости) === | ||
| + | |||
| + | L<sup>K</sup> (f) > n для ФАЛ f, существенно зависящей от всех своих переменных. | ||
| + | |||
| + | === Определение функции Шеннона ''L<sup>π</sup>(n)'' и её верхняя оценка, получаемая с помощью моделирования совершенной ДНФ на основе контактного дерева === | ||
| + | |||
| + | * L<sup>π</sup>(n) = max<sub>ƒ∈P<sub>2</sub>(n)</sub>L<sup>π</sup>(ƒ) | ||
| + | * L<sup>π</sup>(n) ≤ 2<sup>n + 1</sup> − 2 //FIXME | ||
| + | |||
| + | === Нижняя оценка функции Шеннона ''L<sup>c</sup>(n)'' и то мощностное соотношение, из которого она выводится === | ||
| + | |||
| + | * L<sup>C</sup>(n) ≥ 2<sup>n</sup> / n (Асимптотически больше) | ||
| + | * ||U<sup>C</sup>(L,n)|| ≤ (8(L + n))<sup>L + 1</sup> | ||
| + | |||
| + | === Определение ДУМ и формулировка утверждения о свойствах стандартного ДУМ === | ||
| + | |||
| + | * Дизъюнктивно-универсальное множество (ДУМ) ''G'' порядка ''n'' и ранга ''p'' ⇔ ∀ ''g ∈ P<sub>2</sub>(n) ∃ g<sub>1</sub>,...,g<sub>p</sub> ∈ G : g = g<sub>1</sub>∪...∪g<sub>p</sub>'' | ||
| + | |||
| + | '''Утверждение'''. Пусть ''m'', ''S'', ''p'' ∈ ''N'': ''p * S ≥ 2<sup>m</sup>'', тогда ∃ ДУМ ''G'' порядка ''m'' и ранга ''p'': | ||
| + | # |G| ≤ p * 2<sup>S</sup> | ||
| + | # В ''G'' ∃ система из ''p'' ортогональных функций ψ<sub>1</sub>,...,ψ<sub>p</sub> : ∀ g ∈ G имплицирует одну из них. | ||
| + | |||
| + | === Регулярные разбиения единичного куба и моделирование ФАЛ с помощью БП. Асимптотика сложности контактного дешифратора === | ||
| + | |||
| + | Множество δ, δ ⊆ B<sup>q</sup>, называется m-регулярным множеством наборов | ||
| + | куба B<sup>q</sup>, если m < q, |δ| = 2<sup>m</sup> и все префиксы длины m наборов из δ различны. | ||
| + | |||
| + | m-регулярное разбиение куба B<sup>q</sup> — разбиение этого куба, состоящее из m-регулярных множеств δ<sub>1</sub>, …, δ<sub>q − m</sub>. (???) | ||
| + | |||
| + | моделирование ФАЛ с помощью БП - ??? | ||
| + | |||
| + | L<sup>K</sup> (Q<sub>n</sub>) ~ 2<sup>n</sup> | ||
| + | |||
| + | === !!! Асимптотически наилучший метод синтеза КС === | ||
| + | |||
| + | === !!! Построение самокорректирующихся КС === | ||
| + | |||
| + | === !!! Асимптотически наилучший метод синтеза формул в В<sub>0</sub>. Поведение функции Шеннона для глубины ФАЛ === | ||
| + | |||
| + | === !!! Задача синтеза схем для ФАЛ из специальных классов и индивидуальных ФАЛ. Методы получения верхних и нижних оценок сложности, минимальность некоторых схем === | ||
| + | |||
| + | === Определение ''m''-регулярного множества наборов === | ||
| + | Множество δ, δ ⊆ B<sup>q</sup>, называется ''m-регулярным'' множеством наборов куба B<sup>q</sup>, если m < q, |δ| = 2<sup>m</sup> и все префиксы длины m наборов из δ различны. | ||
| + | |||
| + | === !!! Определение (p, q)-самокорректирующейся КС. Утверждение о сложности самокорректирующейся КС, получаемой дублированием === | ||
| + | |||
| + | {{Курс Основы Кибернетики}} | ||
Версия 17:51, 3 февраля 2008
Представление функций с помощью дизъюнктивных нормальных форм. Тесты для таблиц
Определение ЧУМ, его цепи, антицепи, длины и ширины
- Отношение, обладающее свойствами рефлексивности, транзитивности, антисимметричности — отношение частичного порядка
- Если τ — отношение частичного порядка на множестве А, то пара (А,τ) — частично упорядоченное множество (ЧУМ)
- Для ЧУМ (А, τ) множество, состоящее из попарно сравнимых/несравнимых элементов а ∈ А называется цепью/антицепью
- Максимальная мощность цепей/антицепей ЧУМ называется его длиной/шириной
- Цепь С ⊆ А ЧУМ (А, τ) — неуплотняемая, если С представляет собой максимальное по включению множество соответствующего типа
- ЧУМ (А, τ) длины t (|A| = t) называется ранжированным ЧУМ, если все его неуплотняемые цепи имеют мощность t
Определение ранжированного ЧУМ и утверждение о его ширине
- ЧУМ (А,τ) длины t (|A| = t) называется ранжированным ЧУМ, если все его неуплотняемые цепи имеют мощность t.
Утверждение. Если в ранжированном частично упорядоченном множестве (A,τ) через каждые два элемента одного и того же яруса проходит одинаковое число неуплотняемых цепей, то ширина частично упорядоченного множества (A,τ) равна максимальной мощности его ярусов.
Следствие. Ширина ЧУМ (Bn, ≤) равна ![]()
Определение импликанты, простой импликанты и сокращенной ДНФ
- ФАЛ ƒ имплицирует ФАЛ g (или, иначе, ФАЛ g поглощает ФАЛ ƒ) если Nƒ ⊆ Ng, то есть импликация (ƒ → g) тождественно равна 1
- ЭК, которая имплицирует ФАЛ ƒ, называется импликантой этой ФАЛ
- Импликанта К ФАЛ ƒ называется простой импликантой этой ФАЛ, если она не поглощается никакой другой отличной от нее импликантой ФАЛ ƒ
- Дизъюнкция всех простых импликант ФАЛ ƒ называется ее сокращенной ДНФ
Тождество поглощения и определение неприводимой ДНФ
- Тождество поглощения: x1 ∨ x1x2 = x1
- ДНФ U вида U = K1 ∨ ... ∨ Ks называется неприводимой, если соответствующее ей покрытие является неприводимым, т.е. ни одна из граней NK1,...,NKs не содержится ни в одной из других граней покрытия Nƒ = NK1 ∪ ... ∪ NKs
Формулировка утверждения, связанного с построением сокращенной ДНФ из какой-либо КНФ
Утверждение. Если неприводимая ДНФ U получается из КНФ B ФАЛ ƒ в результате раскрытия скобок и приведения подобных, то U — сокращенная ДНФ ФАЛ ƒ.
Тождество обобщенного склеивания и определение нерасширяемой ДНФ
Тождество обобщенного склеивания: xiK‘ ∨ xiK" = xiK‘ ∨ xiK" ∨ K‘K"
- tОС: x1 & x2 ∨ x1 & x3 = x1 & x2 ∨ x1 & x3 ∨ x2 & x3
Формулировка утверждения, связанного с построением сокращенной ДНФ из какой-либо ДНФ
Утверждение. Из любой ДНФ А ФАЛ ƒ можно получить сокращенную ДНФ этой ФАЛ в результате построения последовательных строгих расширений и приведения подобных до получения неприводимой ДНФ, не имеющей строгих расширений.
Определение тупиковой, кратчайшей и минимальной ДНФ
- ДНФ A, реализующая ФАЛ ƒ называется тупиковой, если ƒ ≠ A' для любой A', полученной из A удалением некоторых букв или целых ЭК.
- Минимальная (кратчайшая) ДНФ — ДНФ, которая имеет наименьший ранг (длину) среди всех ДНФ реализующих ФАЛ ƒ.
Определение ядровой точки, ядровой грани и ДНФ Квайна
- Набор α, α ∈ Bn, называется ядровой точкой ФАЛ ƒ(x1,...,xn), если α ∈ Nƒ и α входит только в одну максимальную грань ФАЛ ƒ.
- Грань NK, являющаяся максимальной гранью ФАЛ ƒ и содержащая ядровую точку α, называется ядровой гранью.
- Совокупность всех различных ядровых граней ФАЛ ƒ называется ядром ФАЛ ƒ.
- ДНФ, получающаяся из сокращенной ДНФ ФАЛ ƒ удалением тех ЭК К, для которых грань NK покрывается ядром ФАЛ ƒ, но не входит в него, называется ДНФ Квайна этой ФАЛ.
Определение пучка, регулярной точки и регулярной грани
- Множество всех проходящих через α ( α ∈ Nƒ ) максимальных граней ФАЛ ƒ называется пучком ФАЛ ƒ через точку α (обозначается Πα(ƒ)).
- Точка α, α ∈ Nƒ называется регулярной точкой ФАЛ ƒ, если существует такая точка β, что β ∈ Nƒ и Πβ(f) ⊂ Πα(ƒ).
- Грань NK ФАЛ ƒ называется регулярной гранью этой ФАЛ, если все точки NK регулярны.
Определение ДНФ сумма тупиковых и критерий вхождения в нее простых импликант
- ДНФ сумма тупиковых ФАЛ f - дизъюнкция всех тех различных простых импликант этой ФАЛ, которые входят хотябы в одну тупиковую ДНФ ФАЛ f.
Утверждение. Простая импликанта К ФАЛ f входит в ДНФ ∑T тогда и только тогда, когда грань NK не является регулярной гранью этой ФАЛ.
Определение ДНФ пересечения тупиковых и критерий вхождения в неё простых импликант
- ДНФ пересечение тупиковых ФАЛ ƒ - дизъюнкция всех тех различных простых импликант этой ФАЛ, которые входят в любую тупиковую ДНФ ФАЛ ƒ.
Утверждение. ДНФ пересечение тупиковых ФАЛ ƒ состоит из тех простых импликант ФАЛ ƒ, которые соответствуют ядровым граням этой ФАЛ.
Определение линейной ФАЛ и особенности её ДНФ
- Линейная ФАЛ — это ФАЛ ƒ ∈ P2(n) вида ƒ(x1...xn) = α1x1 ⊕ ... ⊕ αnxn ⊕ α0, где α0,...,αn — булевы константы.
Утверждение. Совершенная ДНФ линейной существенной функции является единственной ДНФ этой ФАЛ от её существенных БП.
Необходимые и достаточные условия единственности представления ФАЛ в виде ДНФ
Утверждение. Совершенная ДНФ ФАЛ ƒ из P2(n) является ее единственной ДНФ тогда и только тогда, когда во множестве Nƒ нет соседних наборов.
Определение монотонной ФАЛ и её нижней единицы. Особенности простых импликант монотонной ФАЛ
- ФАЛ ƒ (x1,...,xn) называется монотонной, если ƒ(α) ≤ ƒ(β) для любых наборов α,β ∈ Bn таких, что α ≤ β.
- Набор α ∈ Bn называется нижней единицей монотонной ФАЛ ƒ, ƒ ∈ P2(n), если α ∈ Nƒ и ƒ(β) = 0 для любого отличного от α набора β такого, что β ≤ α.
- Если ФАЛ ƒ(x1,...,xn) монотонно зависит от БП xi, то ни одна из ее простых импликант не может содержать букву ¬xi
Определение монотонной ФАЛ, формулировка утверждения об особенностях ДНФ для монотонных ФАЛ
- ФАЛ ƒ(x1...xn) называется монотонной, если ƒ(α) ≤ ƒ(β) для любых наборов α и β куба B n таких, что α ≤ β
Утверждение. Сокращенная ДНФ U монотонной ФАЛ ƒ, ƒ ∈ P2(n), является единственной тупиковой ДНФ этой ФАЛ и имеет вид: U(x1...xn) = ∨β∈Nƒ+ Kβ+(x1...xn)
Определение цепной и циклической ФАЛ. Особенности ДНФ циклической ФАЛ, используемые в теореме Журавлева о ДНФ сумма минимальных
- Функция ƒ(x1,...,xn) называется цепной (циклической) функцией длины t, если ее сокращенная ДНФ с "геометрической" точки зрения представляет собой цепь (соответственно цикл) из t полседовательно соединенных ребер N1, N2, ..., Nt куба Bn.
- Цепная ФАЛ ƒ нечетной длины t = 2k - 1 ≥ 3 имеет единственную минимальную ДНФ, которая совпадает с ее ДНФ ΣM и соответствует покрытию N1 ∪ N3 ∪ ... ∪ Nt
Формулировка теоремы Журавлева о ДНФ сумма минимальных
Утверждение (теорема Журавлева). При любом n ∈ Ν, n ≥ 3, в P2(n) существуют ФАЛ ƒ' и ƒ", имеющие общую простую импликанту К, которая входит в ДНФ ∑M одной, но не входит в ДНФ ∑M другой из этих ФАЛ и для которой Sn-3(NK,ƒ') = Sn-3(NK,ƒ").
Определение ФАЛ покрытия матрицы и ее свойства, утверждение о КНФ для ФАЛ покрытия
- Пусть N = {α1,...αs,} - конечное множество, а П = (N1,...,Np) - система его подмножеств, образующих покрытие множества N. Сопоставим паре (N,П) матрицу M ∈ Bp,s, для которой M<i,j> = 1 ⇔ αj ∈ Ni. Будем говорить, что i-я строка матрицы М покрывает ее j-й столбец, если M<i,j> = 1 и что система строк с номерами из I, I ⊆ [1,p], образует покрытие матрицы М, если каждый ее столбец покрывается хотябы одной строкой с номером из I, то есть система подмножеств {Ni}i ∈ I задает покрытие множества N.
- Пусть M ∈ Bp,s - матрица без нулевых столбцов. Сопоставим i-й строке матрицы М БП yi, а каждому набору β ∈ Bp значений этих переменных y = (y1,...,yp) - множество строк матрицы М с намерами из множества I = I(β) ⊆ [1,p], где i ∈ I(β) ⇔ β<i> = 1. ФАЛ F(y), для которой F(β) = 1 ⇔ система строк матрицы М с номерами из I(β) образует ее покрытие, будем называть функцией покрытия матрицы М.
Свойства ФАЛ покрытия матрицы
- монотонность
- ее "нижние единицы" соответствуют тупиковым покрытиям
Утверждение. Функция покрытия F(y1,...,yp) матрицы M ∈ Bp,s без нулевых столбцов задается КНФ вида: 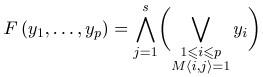 (*)
(*)
Следствие. В результате раскрытия скобок и приведения подобных из КНФ (*) можно получить сокращенную ДНФ ФАЛ F(y), простые импликанты которой взаимно однозначно соответствуют тупиковым покрытиям матрицы М.
Градиентный алгоритм покрытия матрицы и утверждение о длине градиентного покрытия
- Градиентный алгоритм: На каждом шаге алгоритма в матрице выбирается и включается в покрытие такая строка, которая покрывает наибольшее число ещё не покрытых столбцов (если таких строк несколько, из них выбирается строка с наименьшим номером). Алгоритм заканчивается свою работу после того шага, на котором получилось покрытие.
Утверждение. Пусть для действительного γ, 0 < γ ≤ 1, в каждом столбце матрицы M, M ∈ Bp,s, имеется не меньше чем γ•p единиц. Тогда покрытие матрицы M, получаемое с помощью градиентного алгоритма, имеет длину не больше, чем ![]() , где ln+x = ln x, если x ≥ 1 и ln+x = 0, если 0 < x ≤ 1.
, где ln+x = ln x, если x ≥ 1 и ln+x = 0, если 0 < x ≤ 1.
Определение протыкающего множества для граней единичного куба и верхняя оценка его мощности.
- Пусть N = {α1,...αs,} - конечное множество, а П = (N1,...,Np) - система его подмножеств. Множество, протыкающее систему П - такое подмножество множества N,в котором ∀ i ∈ [1,p] имеется хотябы один элемент из Ni.
Утверждение. При любых натуральных n и m, m ≤ n, в кубе Bn всегда найдется множество мощности не более, чем n×2m, протыкающее все грани ранга m.
Определение функции Шеннона R(n) для ранга ДНФ и ее значение.
- R(n) = maxƒ∈P2(n) R(ƒ);
- R(n) = n × 2n − 1
Определение функции Шеннона λ(n) для длины ДНФ и ее значение.
- λ(n) = maxƒ∈P2(n) λ(ƒ);
- λ(n) = 2n − 1
Определение длины ДНФ λ(ƒ) для ФАЛ ƒ и ее оценки для почти всех ФАЛ ƒ от n переменных
- λ(ƒ) = minДНФ U, реализующим f λ(U)
- Для почти всех ФАЛ из P2(n) λ(ƒ)<~ (3/4)*2n − 1
Определение ранга ДНФ R(f) для ФАЛ ƒ и ее оценки для почти всех ФАЛ ƒ от n переменных
- R(f) = minДНФ U, реализующим f R(U)
- Для почти всех ФАЛ из P2(n) R(f)<~ (3/4)*n*2n − 1
Определение проверяющего теста матрицы и его ФАЛ, утверждение и КНФ для ФАЛ проверяющего теста
Пусть есть схема Σ1, которая реализует ФАЛ f1. Пусть есть источник помех И. Под действием источника И схема Σ может переходить в одно из неисправных состояний Σ2, …, Σs, каждое из которых реализует ФАЛ fi, i = 2, s.
Пусть (Σ, И) — модель ненадёжной схемы Σ с возможными состояниями Σ1, …, Σs, в которых реализуются ФАЛ f1, …, fs, определённые на множестве наборов A = {α1, …, αp} ⊆ Bn. Рассмотрим матрицу M ∈ Bp, s, M[i, j] = fj(αi). Множество строк матрицы M с номерами из T ⊆ [1, p] называется проверяющим тестом матрицы M, если для ∀j ∈ 1, s, ∃t ∈ T такое, что M[t, 1] ≠ M[t, j].
Утверждение. Функция проверяющего теста f(y1, …, yp) для отделимой по столбцам матрицы M ∈ Bp, s может быть задана с помощью КНФ
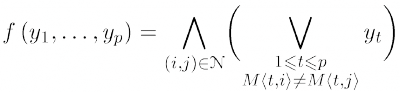
где N = {(1, j) | j ∈ 1, s}
Утверждение об оценке длины диагностического теста для произвольной таблицы с заданным числом столбцов
Утверждение. Длина любого тупикового диагностического теста для отделимой по столбцам матрицы из множества Bp,s заключена в пределах от ⌈log s⌉ до (s − 1)
!!! Описание ЧУМ, антицепями которого являются тупиковые ДНФ.
Ранжированное множество длины (n+1) всех граней n-мерного единичного куба с отношением вложения. (не точно, стр. 63)
Основные классы дискретных управляющих систем. Структурные представления и эквивалентные преобразования схем, оценка их числа
Индуктивное определение формулы и реализуемой ею ФАЛ
Любая переменная xj из X считается формулой глубины 0 над множеством Б, которая реализует функцию xj. Если φ(x1,...,xk) ∈ Б и для каждого i, i ∈ [1,k], определена формула Fi глубины qi над множеством Б, которая реализует функцию ƒi из PA, то запись F вида
F = φ(F1,...,Fk)
является формулой глубины q = max{q1,...,qk} + 1 над Б, которая реализует функцию ƒ вида ƒ = φ(ƒ1,...,ƒk).
Индуктивное определение π-схемы и нахождение реализуемой ею ФАЛ
Простейшей π-схемой считается любая (1,1)-КС, которая состоит из одного контакта, соединяющего полюса. Если π-схемы ∑1 и ∑2 уже определены, то (1,1)-КС ∑1(∑2), которая получается в результате их последовательного (параллельного) соединения тоже является π-схемой.
Определение разделительной по входам (выходам) КС и формулировка леммы Шеннона
КС разделительна по входам (выходам), если ФАЛ проводимости для ∀ различных входов (выходов) ≡ 0.
Лемма Шеннона: Пусть Σ = Σ''(Σ') - результат стыковки ⇒ F ≥ F' × F''. F = F' × F'', если Σ'' разделительна по входам, или Σ' разделительна по выходам.
Определение подсхемы Σ' КС ∑ с указанием особенностей, связанных с объявлением вершин Σ' её полюсами. Основное тождество t4 (введение фиктивной переменной) и вспомогательное тождество t11 (лемма о звезде); обобщенные тождества t4(n) и t11(n)
Определение подсхемы Σ' КС Σ:
Σ' — подсхема схемы Σ ⇔
- V(Σ') ⊆ V(Σ)
- E(Σ') ⊆ E(Σ)
-
- ∀ полюс Σ, вошедший в Σ' — полюс Σ'
- ∀ вершина Σ', инцидентная контакту Σ\Σ' - полюс Σ'
- ∀ другая вершина м. б. полюсом Σ'.
| t4 | |
|---|---|
| t11 | 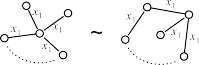
|
Канонический вид КС от БП x1,...,xn и формулировка утверждения о приведении КС от БП x1,...,xn к каноническому виду с помощью основных тождеств.
∑^ /*здесь и далее крышка пишется над сигмой*/ - схема канонического вида ⇔ 1) ∀ контакт ∑^ лежит на стандартной цепи порядка n, явл. подсхемой ∑^ с полюсами в конечных вершинах цепи. 2) ∀ внутренняя вершина ∑^ - внутренняя вершина стандартной цепи 3) в ∑^ отсутствуют висячие циклы и || стандартные цепи 4) в ∑^ нет существенных транзитивных проводимостей /*вопрос +-, комментарий лектора: отсутствует утверждение о переходе к КВ*/
∑^ получается из ∑ удалением ∑' (подсхемы) и заменой ∑' на ∑' ' с соотв. присоединением полюсов, эквив. ∑ (принцип эквивалентной замены).
Определение величины ||Uc(L, n)|| и её верхняя оценка
- Uc(L, n) — множество приведенных СФЭ Σ = Σ(x1, …, xn; z1) над базисом Б0, для которых L(Σ) ≤ L.
- ||Uc(L, n)|| — число попарно неэквивалентных схем в Uc(L, n)
Утверждение. Для любых натуральных n и L выполняется неравенство: ||Uc(L, n)|| ≤ (8(L + n))L + 1.
Определение тождества для формул и его подстановки
Подстановка - вместо переменных функции F(x1, ... , xn) подставляем функции: F(F1, ... ,Fn)
Тождество - t^: F(x)' = F(x) (1)
Если к правой и левой частям (1) применить подстановку, то получим тождество:
где F^' = F^'(F1, ... ,Fn) и F^ = F^(F1, ... ,Fn), которое называется подстановкой для тождества t.
Минимальный набор тождеств, входящих в расширенную основную систему, с помощью которого можно любую формулу преобразовать в формулу с поднятыми отрицаниями
В расширенную основную систему входят следующие тождества: r~осн = {rM, rA, rК, rОП, rD, rПК, tП} /* как обычно, ~ стоит над r */
- rA = {tA&,tA∨}
- rK = {tK&,tK∨}
- rОП = {tОП&,tОП∨}
- rD = {tD&,tD∨}
- rПК = {tПК0, &, tПК0, ∨, tПК1, &, tПК1, ∨}
все тождества описаны тут.
!!! Определение КС от БП x1,...,xn как помеченного графа и ФАЛ проводимости между её вершинами
(параграф 6 главы 2)
Формулировка утверждения о связи между π-схемами и формулами с поднятыми отрицаниями
Любой π-схеме можно сопоставить эквивалентную ей формулу F из UФ с поднятыми отрицаниями такую, что R(F) = L(Σ) и обратно.
!!! Определение эквивалентности КС Σ', Σ" и соответствующего тождества. Основное тождество t2 (перестановка контактов в цепочке) и вспомогательное тождество t8 ("расклейка" двух цепочек длины 2 с общим контактом); обобщенные тождества t2(n) и t8(n)
(параграф 7 главы 2, в самом начале)
!!! Определение суммарного цикломатического числа КС от БП x1,...,xn и формулировка утверждения о его изменениях при применении основных тождеств
(глава 2, стр 72)
Определение структуры CФЭ как графа специального вида и изоморфных СФЭ
Под "абстрактной" схемой понимается сеть, часть пометок которой составляют входные переменные и в каждой вершине которой реализуется функция (столбец из функций) от этих переменных. При этом считается, что сама схема реализует систему (матрицу), состоящую из функций (соответственно столбцов функций), реализованных на её выходах. В качестве выходных пометок схемы используются, как правило, специальные выходные переменные, а схема Sigma с входными переменными (входами) x1,..xn и выходными переменными z1,..zm записывается в виде Sigma=Sigma(x1,..xn; z1,..zn).
Две СФЭ считаются изоморфными, если они изоморфны как помеченные графы, и эквивалентными, если они реализуют равные системы ФАЛ.
Определение ранга, сложности и глубины формулы, утверждение о соотношениях между ними
- R(F) — ранг формулы F — число листьев, связанного с ней дерева
- L(F) — сложность формулы F — число остальных вершин, связанного с ней дерева (не листьев)
- D(F) — глубина формулы F — глубина корня, связанного с ней дерева
- R(F) ≤ L(F) + 1 ≤ 2D(F)
!!! Понятие подформулы и применение тождества к формуле
Минимальный набор тождеств, входящих в расширенную основную систему, с помощью которого формулу с поднятыми отрицаниями можно преобразовать в формулу со следующим порядком применения базисных функций: ¬, &, ∨
- Дистрибутивность t&, ∨D: x1 & (x2 ∨ x3) = (x1 & x2) ∨ (x1 & x3)
- Коммутативность коньюнкции t&К: x1 & x2 = x2 & x1
!!! Определение матрицы ФАЛ, реализуемой КС с p входами и q выходами, определение и свойства матрицы, реализемой КС с m неразделенными полюсами
Глава 2, стр. 57-58
Определение величины ||Uπ(L,n)|| и ее верхняя оценка
- ||Uπ(L,n)|| - число попарно не эквивалентных приведенных π-схем от БП x1,...,xn сложности ≤ L
- ||Uπ(L,n)|| ≤ (16n)L
!!! Определение подстановки тождества для КС, связанной с управляющими БП, и ее применение к КС. Основное тождество t3 (цепь из противоположных контактов) и вспомогательные тождество t10 (замыкание по транзитивности); обобщенные тождества t3(n) и t10(n)
!!! Примеры моделирования основных тождеств для формул в классе СФЭ, примеры тождеств ветвления и снятия для ФЭ и входов СФЭ. Формулировка утверждения о переходе от КПСТ для ЭП формул к КПСТ для ЭП СФЭ
Синтез, сложность и надежность управляющих систем
!!! Определение сложности LC(F) системы ФАЛ F = (ƒ1,...,ƒm) и ее тривиальная нижняя оценка для некоторых систем ФАЛ
Определение функции Шеннона LC(n) и ее верхние оценки, получаемые методом Шеннона и методом О. Б. Лупанова
- LC(n) = maxƒ∈P2(n)LC(ƒ)
- Метод Шеннона: LC(n) <∼ 8•2n/n
- Метод Лупанова: LC(n) ≤ (2n/n)•(1 + (5logn + O(1))/n)
Нижняя оценка функции Шеннона Lπ(n) и то мощностное соотношение, из которого она выводится
- Lπ(n) ≥ 2n / log2n (Асимптотически больше)
- ||Uπ(L,n)|| ≤ (16n)L
Определение мультиплексорной ФАЛ Mn порядка n, утверждение о сложности ее реализации в классах π-схем и формул
Функция вида µn(x1,..xn,y0,..y2n-1) = U (a=(a1,..an)) x1a1...xnanyv(a) называется мультиплексорной функцией (мультиплексором) порядка n, а переменные x=(x1,..xn) называются адресными, y=(y0,..y2n-1) - информационными БП мультиплексора µn.
Lп(µn) <= 3*2n-2, LФ(µn) <= 2n+2-3;
!!! Определение сложности LK(ƒ) ФАЛ ƒ(x1...xn) в классе КС и её тривиальные нижние оценки для ФАЛ ƒ, существенно зависящей от всех своих переменных (с учетом характера этой зависимости)
LK (f) > n для ФАЛ f, существенно зависящей от всех своих переменных.
Определение функции Шеннона Lπ(n) и её верхняя оценка, получаемая с помощью моделирования совершенной ДНФ на основе контактного дерева
- Lπ(n) = maxƒ∈P2(n)Lπ(ƒ)
- Lπ(n) ≤ 2n + 1 − 2 //FIXME
Нижняя оценка функции Шеннона Lc(n) и то мощностное соотношение, из которого она выводится
- LC(n) ≥ 2n / n (Асимптотически больше)
- ||UC(L,n)|| ≤ (8(L + n))L + 1
Определение ДУМ и формулировка утверждения о свойствах стандартного ДУМ
- Дизъюнктивно-универсальное множество (ДУМ) G порядка n и ранга p ⇔ ∀ g ∈ P2(n) ∃ g1,...,gp ∈ G : g = g1∪...∪gp
Утверждение. Пусть m, S, p ∈ N: p * S ≥ 2m, тогда ∃ ДУМ G порядка m и ранга p:
- |G| ≤ p * 2S
- В G ∃ система из p ортогональных функций ψ1,...,ψp : ∀ g ∈ G имплицирует одну из них.
Регулярные разбиения единичного куба и моделирование ФАЛ с помощью БП. Асимптотика сложности контактного дешифратора
Множество δ, δ ⊆ Bq, называется m-регулярным множеством наборов куба Bq, если m < q, |δ| = 2m и все префиксы длины m наборов из δ различны.
m-регулярное разбиение куба Bq — разбиение этого куба, состоящее из m-регулярных множеств δ1, …, δq − m. (???)
моделирование ФАЛ с помощью БП - ???
LK (Qn) ~ 2n
!!! Асимптотически наилучший метод синтеза КС
!!! Построение самокорректирующихся КС
!!! Асимптотически наилучший метод синтеза формул в В0. Поведение функции Шеннона для глубины ФАЛ
!!! Задача синтеза схем для ФАЛ из специальных классов и индивидуальных ФАЛ. Методы получения верхних и нижних оценок сложности, минимальность некоторых схем
Определение m-регулярного множества наборов
Множество δ, δ ⊆ Bq, называется m-регулярным множеством наборов куба Bq, если m < q, |δ| = 2m и все префиксы длины m наборов из δ различны.
!!! Определение (p, q)-самокорректирующейся КС. Утверждение о сложности самокорректирующейся КС, получаемой дублированием


