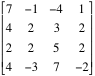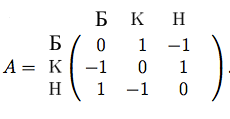Тигры, контрольная 1
Материал из eSyr's wiki.
| Строка 2: | Строка 2: | ||
в 2012 году лектор дал всего две задачи. В обеих был параметр '''N''', который на самом деле мало на что влиял. Его надо было посчитать как сумму длин составляющих вашего ФИО, то есть для '''Потапенко Виктор Алексеевич''' '''N''' = 25. Оценка складывалась из 2 за присутствие и по 1,5 за каждую из задач (за каждый из трех подпунктов первой задачи по 0,5). При неправильно посчитанном '''N''' лектор ставил 2. В проходе аудитории (П8) стоял стол, который мешал ходить, и, возможно поэтому, лектор не ходил и не проверял валидность конспектов, отсутствие телефонов и пр. На все давалось примерно 20 минут | в 2012 году лектор дал всего две задачи. В обеих был параметр '''N''', который на самом деле мало на что влиял. Его надо было посчитать как сумму длин составляющих вашего ФИО, то есть для '''Потапенко Виктор Алексеевич''' '''N''' = 25. Оценка складывалась из 2 за присутствие и по 1,5 за каждую из задач (за каждый из трех подпунктов первой задачи по 0,5). При неправильно посчитанном '''N''' лектор ставил 2. В проходе аудитории (П8) стоял стол, который мешал ходить, и, возможно поэтому, лектор не ходил и не проверял валидность конспектов, отсутствие телефонов и пр. На все давалось примерно 20 минут | ||
| - | + | ==Теория== | |
'''Седловая точка''' матрицы - это формально такой элемент матрицы, что в своем столбце он самый большой (один из самых больших, т.е. не строго >), а в своей строке он один из самых маленьких. Например в матрице | '''Седловая точка''' матрицы - это формально такой элемент матрицы, что в своем столбце он самый большой (один из самых больших, т.е. не строго >), а в своей строке он один из самых маленьких. Например в матрице | ||
| Строка 8: | Строка 8: | ||
[[Изображение:Tig2.png]] | [[Изображение:Tig2.png]] | ||
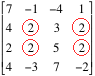
| - | седловая точка - это элемент в первом столбце второй строке, так как он >= всех остальных элементов первого столбца и <= всех остальных элементов второй строки | + | седловая точка - это элемент в первом столбце второй строке, так как он >= всех остальных элементов первого столбца и <= всех остальных элементов второй строки. Довольно просто показать, что если у матрицы несколько седловых точек, то все их значения равны. Для поиска всех седловых точек в матрицах большой размерности не нужно рассматривать каждый элемент отдельно, можно воспользоваться алгоритмом, опирающимся на вспомогательную теорему. Работу алгоритма покажем на примере поиска всех седловых точек матрицы |
| + | |||
| + | [[Изображение:Tig3.png]] | ||
| + | |||
| + | Соберем наименьшие значения по всем строкам, получим '''(-4, 2, 2, -3)'''. Также соберем наибольшие значения по всем столбцам '''(7, 2, 7, 2)'''. Проверим, равно ли наибольшее из чисел первого набора наименьшему числу из второго набора. В нашем случае это так и это число 2. Если бы оказалось, что максимум первого набора меньше, чем минимум второго, то седловых точек не было бы. А ситуации, что максимум первого набора больше минимума второго вообще быть не может, доказывается отдельно. Итак, теперь посмотрим, на каких позициях стоят 2-ки в наших наборах. В первом это '''{2, 3}''', а во втором это '''{2, 4}'''. На произведении этих множеств и располагаются все седловые точки (то есть '''{2, 3}''' X '''{2, 4}''' = { '''{2, 2}''', '''{3, 2}''', '''{2, 4}''', '''{3, 4}''' } ) | ||
| + | |||
| + | [[Изображение:Tig4.png]] | ||
| + | |||
| + | Но причем здесь теория игр? Дело в том что при игре один-на-один, когда интересы игроков прямо противоположны мы пользуемся матрицами стратегий и понятием седловых точек. Например при игре в "камень ножницы бумага" матрица стратегий выглядит так | ||
| + | |||
| + | [[Изображение:Tig5.png]] | ||
| + | |||
| + | где стратегия - это непосредственно выбор камня, ножниц или бумаги, а на пересечениях стратегий выигрыш первого игрока. первый игрок выбирает строку, второй выбирает столбец. | ||
Версия 23:12, 6 октября 2012
Описание
в 2012 году лектор дал всего две задачи. В обеих был параметр N, который на самом деле мало на что влиял. Его надо было посчитать как сумму длин составляющих вашего ФИО, то есть для Потапенко Виктор Алексеевич N = 25. Оценка складывалась из 2 за присутствие и по 1,5 за каждую из задач (за каждый из трех подпунктов первой задачи по 0,5). При неправильно посчитанном N лектор ставил 2. В проходе аудитории (П8) стоял стол, который мешал ходить, и, возможно поэтому, лектор не ходил и не проверял валидность конспектов, отсутствие телефонов и пр. На все давалось примерно 20 минут
Теория
Седловая точка матрицы - это формально такой элемент матрицы, что в своем столбце он самый большой (один из самых больших, т.е. не строго >), а в своей строке он один из самых маленьких. Например в матрице
седловая точка - это элемент в первом столбце второй строке, так как он >= всех остальных элементов первого столбца и <= всех остальных элементов второй строки. Довольно просто показать, что если у матрицы несколько седловых точек, то все их значения равны. Для поиска всех седловых точек в матрицах большой размерности не нужно рассматривать каждый элемент отдельно, можно воспользоваться алгоритмом, опирающимся на вспомогательную теорему. Работу алгоритма покажем на примере поиска всех седловых точек матрицы
Соберем наименьшие значения по всем строкам, получим (-4, 2, 2, -3). Также соберем наибольшие значения по всем столбцам (7, 2, 7, 2). Проверим, равно ли наибольшее из чисел первого набора наименьшему числу из второго набора. В нашем случае это так и это число 2. Если бы оказалось, что максимум первого набора меньше, чем минимум второго, то седловых точек не было бы. А ситуации, что максимум первого набора больше минимума второго вообще быть не может, доказывается отдельно. Итак, теперь посмотрим, на каких позициях стоят 2-ки в наших наборах. В первом это {2, 3}, а во втором это {2, 4}. На произведении этих множеств и располагаются все седловые точки (то есть {2, 3} X {2, 4} = { {2, 2}, {3, 2}, {2, 4}, {3, 4} } )
Но причем здесь теория игр? Дело в том что при игре один-на-один, когда интересы игроков прямо противоположны мы пользуемся матрицами стратегий и понятием седловых точек. Например при игре в "камень ножницы бумага" матрица стратегий выглядит так
где стратегия - это непосредственно выбор камня, ножниц или бумаги, а на пересечениях стратегий выигрыш первого игрока. первый игрок выбирает строку, второй выбирает столбец.