Методы Оптимизации, Теормин
Материал из eSyr's wiki.
(→Определения индивидуальной и массовой задачи, кодировки задачи, алгоритма решения массовой задачи, временной сложности алгоритма.) |
(→Определения индивидуальной и массовой задачи, кодировки задачи, алгоритма решения массовой задачи, временной сложности алгоритма.) |
||
| Строка 8: | Строка 8: | ||
P есть множество индивидуальных задач <math>I \in P</math>. Индивидуальная задача получается, всем всем параметрам присвоить конкретные значения. | P есть множество индивидуальных задач <math>I \in P</math>. Индивидуальная задача получается, всем всем параметрам присвоить конкретные значения. | ||
| + | |||
Пусть E - конечный алфавит, а E* - множество слов в этом алфавите. Отображение e: <math>P \rightarrow E*</math> называется кодировкой задачи П. | Пусть E - конечный алфавит, а E* - множество слов в этом алфавите. Отображение e: <math>P \rightarrow E*</math> называется кодировкой задачи П. | ||
| + | |||
'''Алгоритм А решает массовую задачу''' П, если для любой <math>I \in P</math> : А применим к I, то есть останавливается за конечное число шагов . | '''Алгоритм А решает массовую задачу''' П, если для любой <math>I \in P</math> : А применим к I, то есть останавливается за конечное число шагов . | ||
| - | Кодировка задачи P: | + | '''Кодировка задачи P''': |
| - | Отобраение | + | Отобраение <math>e: P \rightarrow E* </math>, обладающее следующими свойствами: |
| + | |||
| + | * Возможность однозначно декодировать, то есть у двух различных ИЗ не может быть одинаковых кодировок. | ||
| + | * <math>e, e^{-1}</math> -- полиномиально вычислимы | ||
| + | * Кодировка не избыточна, то есть для любой другой кодировки <math>e_1</math>, удовлетворяющей 1 и 2 условиям справедливо: | ||
| + | <math>\exists p(.): \forall I 'in P |e(I)| < p(e_{1}(I))</math> | ||
| + | |||
| + | '''Язык массовой задачи''' -- это множество правильных слов, то есть слов, соответствующих ИЗ, имеющим положительный ответ(подразумевается задача распознавания): | ||
| + | <math>L(P, e) = e(Y(P)) = {\sigma \in E*| \sigma = e(I), I \n Y(I)}</math> | ||
| + | |||
| + | '''Язык алгоритма''' -- множество слов, принимаемых А | ||
| + | |||
| + | Алгоритм A '''решает''' массовую задачу П, с кодировкой e, если <math>L(e, P) = L(A)</math> | ||
| + | |||
| + | <math>t{A}(\sigma)</math> - число шагов алгоритма А для входа<math>\sigma \in E*</math> (число шагов). | ||
| - | + | Временная сложность <math>TA(n) = max {tA(\sigma)} \sigma /in E*& |\sigma| < n</math>. | |
Версия 06:35, 7 июня 2009
Теормин
Определения индивидуальной и массовой задачи, кодировки задачи, алгоритма решения массовой задачи, временной сложности алгоритма.
Массовая задача П:
- список свободных параметров;
- формулировка свойств, которым должно удовлетворять решение задачи.
P есть множество индивидуальных задач 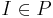 . Индивидуальная задача получается, всем всем параметрам присвоить конкретные значения.
. Индивидуальная задача получается, всем всем параметрам присвоить конкретные значения.
Пусть E - конечный алфавит, а E* - множество слов в этом алфавите. Отображение e: 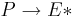 называется кодировкой задачи П.
называется кодировкой задачи П.
Алгоритм А решает массовую задачу П, если для любой 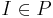 : А применим к I, то есть останавливается за конечное число шагов .
: А применим к I, то есть останавливается за конечное число шагов .
Кодировка задачи P:
Отобраение  , обладающее следующими свойствами:
, обладающее следующими свойствами:
- Возможность однозначно декодировать, то есть у двух различных ИЗ не может быть одинаковых кодировок.
- e,e − 1 -- полиномиально вычислимы
- Кодировка не избыточна, то есть для любой другой кодировки e1, удовлетворяющей 1 и 2 условиям справедливо:
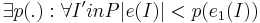
Язык массовой задачи -- это множество правильных слов, то есть слов, соответствующих ИЗ, имеющим положительный ответ(подразумевается задача распознавания): Невозможно разобрать выражение (неизвестная ошибка\n): L(P, e) = e(Y(P)) = {\sigma \in E*| \sigma = e(I), I \n Y(I)}
Язык алгоритма -- множество слов, принимаемых А
Алгоритм A решает массовую задачу П, с кодировкой e, если L(e,P) = L(A)
tA(σ) - число шагов алгоритма А для входа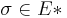 (число шагов).
(число шагов).
Временная сложность Невозможно разобрать выражение (неизвестная ошибка): TA(n) = max {tA(\sigma)} \sigma /in E*& |\sigma| < n .


