МОТП, Задачи на экзамене
Материал из eSyr's wiki.
(Новая: За нерешение данных задач оценка снижается на балл. 1. Даны р точек в двухмерном пространстве (буду пр...) |
|||
| Строка 2: | Строка 2: | ||
1. Даны р точек в двухмерном пространстве (буду прямо их ручкой у вас на листочке задавать). Найти методом главных компонент первую главную компоненту. Так что вспоминайте как матрицу 2х2 к главным осям приводить и ковариации считать. | 1. Даны р точек в двухмерном пространстве (буду прямо их ручкой у вас на листочке задавать). Найти методом главных компонент первую главную компоненту. Так что вспоминайте как матрицу 2х2 к главным осям приводить и ковариации считать. | ||
| + | |||
'''Решение:''' | '''Решение:''' | ||
2. Как метко заметил Оверрайдер, будут задачки на поиск оценки максимального правдоподобия. Насложные, но чтобы было интереснее, не с нормальным распределением. Что-нибудь типа найти оценку МП на параметр распределения Лапласа. | 2. Как метко заметил Оверрайдер, будут задачки на поиск оценки максимального правдоподобия. Насложные, но чтобы было интереснее, не с нормальным распределением. Что-нибудь типа найти оценку МП на параметр распределения Лапласа. | ||
| + | |||
'''Решение:''' | '''Решение:''' | ||
3. Обязательно кому-то дам задачку на условную максимизацию квадратичной функции с линейным ограничением в виде равенства. Писанины там немного, но вот без правила множителей Лагранжа обойтись вряд ли удастся. | 3. Обязательно кому-то дам задачку на условную максимизацию квадратичной функции с линейным ограничением в виде равенства. Писанины там немного, но вот без правила множителей Лагранжа обойтись вряд ли удастся. | ||
| + | |||
'''Решение:''' | '''Решение:''' | ||
| - | 4. Даны 3-4 точки в двухмерном пространстве - одна координата, это х, другая - t. Задача построить по ним линейную регрессию вида \hat{t}=kx+b, т.е. найти коэффициенты k и b. | + | 4. Даны 3-4 точки в двухмерном пространстве - одна координата, это х, другая - t. Задача построить по ним линейную регрессию вида <math>\hat{t}=kx+b</math>, т.е. найти коэффициенты <math>k</math> и <math>b</math>. |
| + | |||
'''Решение:''' | '''Решение:''' | ||
| + | |||
| + | <math>E(T,X,k,b)=\sum_{i=1}^n(t_i-kx_i-b)^2</math> | ||
| + | |||
| + | <math>\frac{\partial E(T,X,k,b)}{\partial k}=2\sum_{i=1}^n(t_i-kx_i-b)(-x_i)=0</math> | ||
| + | |||
| + | <math>\frac{\partial E(T,X,k,b)}{\partial b}=2\sum_{i=1}^n(t_i-kx_i-b)(-1)=0</math> | ||
| + | |||
| + | <math>\frac{1}{n}\sum_{i=1}^n(t_i-kx_i)=b</math> | ||
| + | |||
| + | <math>\sum_{i=1}^n(t_i-kx_i)x_i=0</math> | ||
| + | |||
| + | <math>k \left(\sum_{i=1}^nx_i^2-\frac{1}{n}\left(\sum_{i=1}^nx_i\right)^2\right)=\sum_{i=1}^nt_ix_i-\frac{1}{n}\left(\sum_{i=1}^nx_i\right)\left(\sum_{i=1}^nt_i\right)</math> | ||
| + | |||
| + | Подставляем значения для <math>x_i</math> и <math>t_i</math>, получаем <math>k</math>, затем <math>b</math>. Другой вариант - посчитать напрямую <math>(k,b)=(X^TX)^{-1}X^TY</math>, где <math>X</math> - матрица, первый столбец которой составлен из <math>x_i</math>, второй - из единиц, а <math>Y</math> - столбец из <math>t_i</math>. | ||
Версия 21:56, 25 мая 2009
За нерешение данных задач оценка снижается на балл.
1. Даны р точек в двухмерном пространстве (буду прямо их ручкой у вас на листочке задавать). Найти методом главных компонент первую главную компоненту. Так что вспоминайте как матрицу 2х2 к главным осям приводить и ковариации считать.
Решение:
2. Как метко заметил Оверрайдер, будут задачки на поиск оценки максимального правдоподобия. Насложные, но чтобы было интереснее, не с нормальным распределением. Что-нибудь типа найти оценку МП на параметр распределения Лапласа.
Решение:
3. Обязательно кому-то дам задачку на условную максимизацию квадратичной функции с линейным ограничением в виде равенства. Писанины там немного, но вот без правила множителей Лагранжа обойтись вряд ли удастся.
Решение:
4. Даны 3-4 точки в двухмерном пространстве - одна координата, это х, другая - t. Задача построить по ним линейную регрессию вида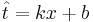 
, т.е. найти коэффициенты k и b.
Решение:
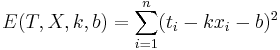
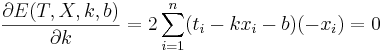
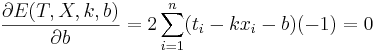
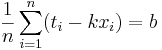
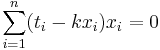
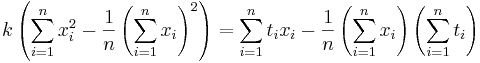
Подставляем значения для xi и ti, получаем k, затем b. Другой вариант - посчитать напрямую (k,b) = (XTX) − 1XTY, где X - матрица, первый столбец которой составлен из xi, второй - из единиц, а Y - столбец из ti.
