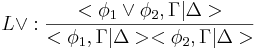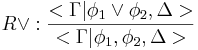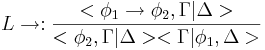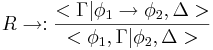Математическая Логика, решение задач/variant 2004
Материал из eSyr's wiki.
(→Задача 4) |
(→Задача 6) |
||
| (6 промежуточных версий не показаны.) | |||
| Строка 42: | Строка 42: | ||
φ<sub>2</sub> = ∃ p (A(p, y) & (p ≤ 0)) | φ<sub>2</sub> = ∃ p (A(p, y) & (p ≤ 0)) | ||
| - | ∀ y (S(y) & φ<sub>1</sub> → φ<sub>2</sub>) | + | ∀ y (S(y) & φ<sub>1</sub> & (S(y) & φ<sub>1</sub> → φ<sub>2</sub>)) |
=== Задача 5 === | === Задача 5 === | ||
''Каковы бы ни были две последовательности действительных чисел такие, что первая одна из них → 0, а другая ограничена, тогда из произведение тоже → 0.'' | ''Каковы бы ни были две последовательности действительных чисел такие, что первая одна из них → 0, а другая ограничена, тогда из произведение тоже → 0.'' | ||
| - | φ<sub>1</sub> = ∀ n (N(n) & ∃ x | + | φ<sub>1</sub> = ∃ M (R(M) & ∀ n (N(n) & ∃ x (R(x) & E(x, n, y) & (|x| < M)))) |
φ<sub>2</sub> = ∃ y<sub>3</sub> (S(y<sub>3</sub>) & ∀ n (N(n) ∃ x<sub>1</sub> ∃ x<sub>2</sub> ∃ x<sub>3</sub> (E(x<sub>1</sub>, n, y<sub>1</sub>) & E(x<sub>2</sub>, n, y<sub>2</sub>) & E(x<sub>3</sub>, n, y<sub>3</sub>) & (x<sub>3</sub> = x<sub>1</sub> × x<sub>2</sub>)))) | φ<sub>2</sub> = ∃ y<sub>3</sub> (S(y<sub>3</sub>) & ∀ n (N(n) ∃ x<sub>1</sub> ∃ x<sub>2</sub> ∃ x<sub>3</sub> (E(x<sub>1</sub>, n, y<sub>1</sub>) & E(x<sub>2</sub>, n, y<sub>2</sub>) & E(x<sub>3</sub>, n, y<sub>3</sub>) & (x<sub>3</sub> = x<sub>1</sub> × x<sub>2</sub>)))) | ||
| Строка 55: | Строка 55: | ||
''Нет такой сходящейся последовательности, что ее нельзя было бы представить как сумму двух сходящихся последовательностей.'' | ''Нет такой сходящейся последовательности, что ее нельзя было бы представить как сумму двух сходящихся последовательностей.'' | ||
| - | φ<sub>1</sub>(y) = S(y) & ∃ m (R(m) & (m, y)) | + | φ<sub>1</sub>(y) = S(y) & ∃ m (R(m) & M(m, y)) |
| - | φ<sub>2</sub>(y<sub>1</sub>, y<sub>2</sub>, y<sub>3</sub>) = (S(y<sub>3</sub>) & ∀ n (N(n) ∃ x<sub>1</sub> ∃ x<sub>2</sub> ∃ x<sub>3</sub> (E(x<sub>1</sub>, n, y<sub>1</sub>) & E(x<sub>2</sub>, n, y<sub>2</sub>) & E(x<sub>3</sub>, n, y<sub>3</sub>) & (x<sub>3</sub> = x<sub>1</sub> | + | φ<sub>2</sub>(y<sub>1</sub>, y<sub>2</sub>, y<sub>3</sub>) = (S(y<sub>3</sub>) & ∀ n (N(n) ∃ x<sub>1</sub> ∃ x<sub>2</sub> ∃ x<sub>3</sub> (E(x<sub>1</sub>, n, y<sub>1</sub>) & E(x<sub>2</sub>, n, y<sub>2</sub>) & E(x<sub>3</sub>, n, y<sub>3</sub>) & (x<sub>3</sub> = x<sub>1</sub> + x<sub>2</sub>)))) |
| - | ¬(∃ y (φ<sub>1</sub>(y) & ∀ y<sub>1</sub> ∀ y<sub>2</sub> (φ<sub>1</sub>(y<sub>1</sub>) & φ<sub>1</sub>(y<sub>2</sub>) & ¬φ<sub>2</sub>(y<sub>1</sub>, y<sub>2</sub>, y)))) | + | ¬(∃ y<sub>3</sub> (φ<sub>1</sub>(y) & ∀ y<sub>1</sub> ∀ y<sub>2</sub> (φ<sub>1</sub>(y<sub>1</sub>) & φ<sub>1</sub>(y<sub>2</sub>) & ¬φ<sub>2</sub>(y<sub>1</sub>, y<sub>2</sub>, y<sub>3</sub>)))) |
== Табличный вывод == | == Табличный вывод == | ||
Текущая версия
Содержание |
[править] Построение предиката по утверждению
[править] Условные обозначения
- почти все = все, кроме конечного числа;
[править] Доступные предикаты
- R(x) — вещественное число;
- N(x) — натуральное число;
- S(y) — y — последовательность действительных чисел;
- E(x, n, y) — x — элемент y с номером n;
- A(p, y) — p — предельная точка последовательности y;
- M(x, y) — x — предел последовательности y;
- x < y, x = y — сравнение и равенство.
[править] Задача 1
Какова бы ни была последовательность действительных чисел и отрезок [a, b] действительных чисел, если бесконечно много элементов этой последовательности содержится в данном отрезке, то хотя бы одна предельная точка данной последовательности также сожержится в этом отрезке.
φ1 = (R(a) & R(b) & (a ≤ b)) φ2 = ∀ n1 (N(n1) & ∃ n2 (N(n2) & (n2 ≥ n1) & ∃ x1 (E(x1, n2, y) & ((a ≤ x1) & (x1 ≤ b)))) φ3 = ∃ p (A(p, y) & ((a ≤ p) & (p ≤ b))) ∀ a ∀ b ∀ y (S(y) & φ1 & φ2 & (S(y) & φ1 & φ2 → φ3))
[править] Задача 2
Какова бы ни была последовательность действительных чисел, найдется отрезок, содержащий все ее предельные точки.
∀ y S(y) & ∃ a ∃ b (R(a) & R(b) & (a ≤ b) ∀ p (A(p, y) & (a ≤ p) & (p ≤ b))))
[править] Задача 3
Каков бы ни был отрезок [a,b] действительных чисел, если почти все элементы произвольной последовательности действительных чисел лежат вне этого отрезка, то и все предельные точки этой последовательности лежат вне этого отрезка.
φ1 = (R(a) & R(b) & (a ≤ b)) φ2 = ∃ n1 (N(n1) & ∀ n2 (N(n2) & (n2 ≥ n1) & ∀ x1 (E(x1, n2, y) & ((a > x1) ∨ (x1 > b)))) φ3 = ∀ p (A(p, y) & ((a > p) & (p > b))) ∀ a ∀ b ∀ y (S(y) & φ1 & φ2 & (S(y) & φ1 & φ2 → φ3))
[править] Задача 4
Какова бы ни была последовательность действительных чисел, если эта последовательность содержит отрицательный элемент, то найдется хотя бы одна неположительная предельная точка этой последовательности.
φ1 = ∃ x ∃ n (R(x) & N(n) & E(x, n, y) & (x < 0)) φ2 = ∃ p (A(p, y) & (p ≤ 0)) ∀ y (S(y) & φ1 & (S(y) & φ1 → φ2))
[править] Задача 5
Каковы бы ни были две последовательности действительных чисел такие, что первая одна из них → 0, а другая ограничена, тогда из произведение тоже → 0.
φ1 = ∃ M (R(M) & ∀ n (N(n) & ∃ x (R(x) & E(x, n, y) & (|x| < M)))) φ2 = ∃ y3 (S(y3) & ∀ n (N(n) ∃ x1 ∃ x2 ∃ x3 (E(x1, n, y1) & E(x2, n, y2) & E(x3, n, y3) & (x3 = x1 × x2)))) ∀ y1 ∀ y2 (S(y1) & S(y2) & M(0, y1) & φ1 & φ2 & (S(y1) & S(y2) & M(0, y) & φ1 & φ2 → M(0, y3)))
[править] Задача 6
Нет такой сходящейся последовательности, что ее нельзя было бы представить как сумму двух сходящихся последовательностей.
φ1(y) = S(y) & ∃ m (R(m) & M(m, y)) φ2(y1, y2, y3) = (S(y3) & ∀ n (N(n) ∃ x1 ∃ x2 ∃ x3 (E(x1, n, y1) & E(x2, n, y2) & E(x3, n, y3) & (x3 = x1 + x2)))) ¬(∃ y3 (φ1(y) & ∀ y1 ∀ y2 (φ1(y1) & φ1(y2) & ¬φ2(y1, y2, y3))))
[править] Табличный вывод
[править] Правила
[править] Дополнительные правила
-
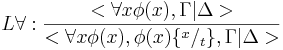 , при условии, что переменная x свободна в φ(x) для терма t.
, при условии, что переменная x свободна в φ(x) для терма t.
-
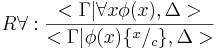 , где c — константа, которая не содержитсяв Γ, Δ или φ(x)
, где c — константа, которая не содержитсяв Γ, Δ или φ(x)
-
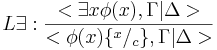 , где c — константа, которая не содержитсяв Γ, Δ или φ(x)
, где c — константа, которая не содержитсяв Γ, Δ или φ(x)
-
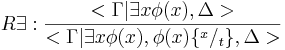 , при условии, что переменная x свободна в φ(x) для терма t.
, при условии, что переменная x свободна в φ(x) для терма t.
[править] Задача 1
С помощью метода семантических таблиц установить, общезначима ли формула:
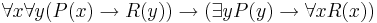
Решение.
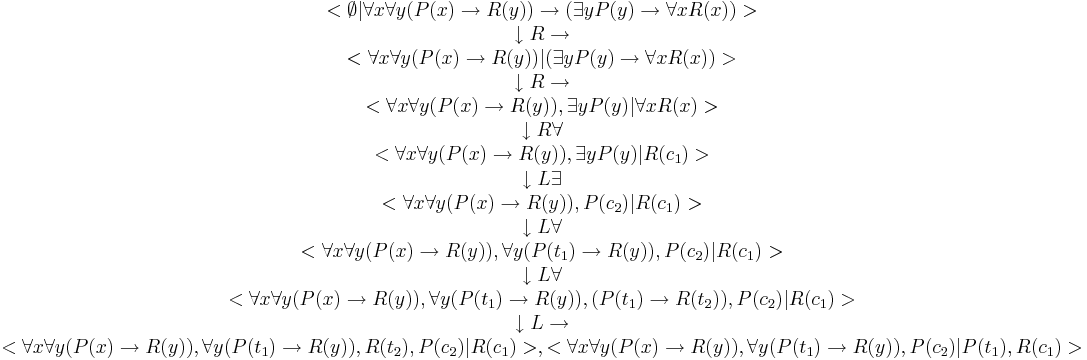
Вторая таблица открыта, следовательно, формула не общезначима. (А разве нельзя провести унификацию терма t_2 = c_1, а t_1 = c_2?)
[править] Задача 2
С помощью метода семантических таблиц установить, общезначима ли формула:
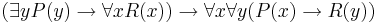
Решение.
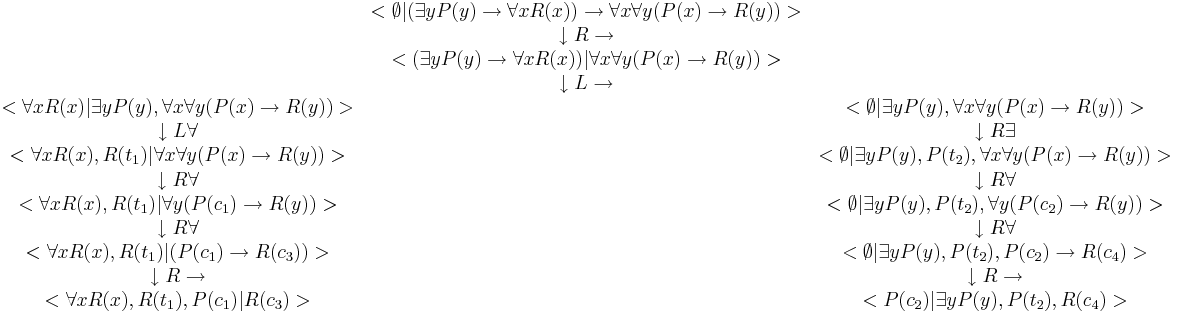
Вторая таблица открыта, следовательно, формула не общезначима. (Аналогично унифицировав t_1 = c_3 и t_2 = c_2 мы получим закрытую таблицу).
[править] Метод резолюций
[править] Задача 1
С помощью метода резолюций исследовать на противоречивость систему дизъюнктов S.
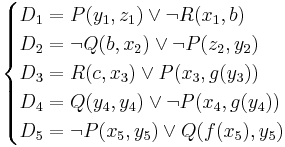
Решение.
(2)и(((1)и(5))и(3)) склеить в !(z2, g(b)), (1)и(3) склеить в P(b, g(b)).
![\begin{array}{l}
D^'_1 - D_1, D_5: R(x_1, b)\lor Q(f(x_5), x_5) \\
D^'_2 - D^'_1, D_3: P(b, g(y_3))\lor Q(f(x_5), x_5) \\
D^'_3 - D_2, D_4: \neg P(z_2, y_2) \lor \neg P(x_4, g(y_4)) \\
D^'_4 - D^'_3: \neg P(z_2, y_2) \\
D^'_5 - D_1, D_3: P(b, y_3)\lor P(y_1, z_1) \\
D^'_6 - D_1, D_3: P(b, y_3) \\
D^'_7 - D^'_4, D^'_6: []
\end{array}](/w/images/math/3/1/b/31bba8c9c118bc604adc0d7255b52ed5.png)
|
|
Ссылки
Официальная страница курса | Задачи
Проведение экзамена | Решение задач: Решение задач методички | Решение задач варианта экзамена 2004 года | Алгоритмы решения задач