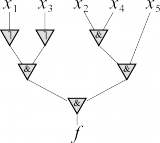Основы Кибернетики, Алгоритмы решения задач/Задачи на эквивалентные преобразования и структурное моделирование
Материал из eSyr's wiki.
(Различия между версиями)
м (1 версий) |
(→По заданной формуле построить подобную ей формулу минимальной глубины.) |
||
| (2 промежуточные версии не показаны) | |||
| Строка 94: | Строка 94: | ||
Тогда ''h''<sub>i</sub> = ⌈log<sub>2</sub>(''n'' + ''m'')⌉ — минимальная возможная глубина реализации ЭК. | Тогда ''h''<sub>i</sub> = ⌈log<sub>2</sub>(''n'' + ''m'')⌉ — минимальная возможная глубина реализации ЭК. | ||
| - | Раскроем у формулы все скобки и поднимем отрицания, после чего упорядочим в полученной ДНФ элементарные конъюнкции в порядке убывания их высоты. Далее построим каждую ЭК и начнём объединять их в дизъюнкции справа налево. В результате должна получиться СФЭ с минимальной глубиной. | + | <s>Раскроем у формулы все скобки и поднимем отрицания, после чего упорядочим в полученной ДНФ элементарные конъюнкции в порядке убывания их высоты. Далее построим каждую ЭК и начнём объединять их в дизъюнкции справа налево. В результате должна получиться СФЭ с минимальной глубиной.</s> Этого делать нельзя, т.к. строится подобная формула. |
<!-- Рисуем дерево глубины h, заменяя в нем самые левые ветки с парами листьев на отрицания переменных, далее листья на сами переменные, затем просто забиваем свободные листья единицами, а узлы — конъюнкциями, после чего проводим оптимизацию правой части по принципу s & 1 = s --> | <!-- Рисуем дерево глубины h, заменяя в нем самые левые ветки с парами листьев на отрицания переменных, далее листья на сами переменные, затем просто забиваем свободные листья единицами, а узлы — конъюнкциями, после чего проводим оптимизацию правой части по принципу s & 1 = s --> | ||
Текущая версия
[править] По заданным эквивалентным формулам или КС построить эквивалентное преобразование, переводящее их друг в друга с помощью основных тождеств.
[править] Основные тождества
[править] Для формул
- Ассоциативность
- t&A: x1 & (x2 & x3) = (x1 & x2) & x3
- t∨A: x1 ∨ (x2 ∨ x3) = (x1 ∨ x2) ∨ x3
- Коммутативность
- t&К: x1 & x2 = x2 & x1
- t∨К: x1 ∨ x2 = x2 ∨ x1
- Отождествление базовых переменных
- t&ОП: x2 & x2 = x2
- t∨ОП: x2 ∨ x2 = x2
- Дистрибутивность
- t&, ∨D: x1 & (x2 ∨ x3) = (x1 & x2) ∨ (x1 & x3)
- правила де Моргана
- t¬M: x = x
- t&M: (x1 & x2) = x1 ∨ x2
- t∨M: (x1 ∨ x2) = x1 & x2
- Тождества подстановки констант
- t0, &ПК: x1 & (x2 & x2) = x2 & x2
- t0, ∨ПК: x1 ∨ x2 & x2 = x1
- t1, &ПК: x1 & (x2 ∨ x2) = x1
- t1, ∨ПК: x1 ∨ (x2 ∨ x2) = x2 ∨ x2
- Тождество поглощения
- tП: x1 ∨ x1 & x2 = x1
- Тождество обобщённого склеивания
- tОС: x1 & x2 ∨ x1 & x3 = x1 & x2 ∨ x1 & x3 ∨ x2 & x3
[править] Для контактных схем
[править] Основные тождества
| t1: | |
|---|---|
| t2: | |
| t3: | |
| t4: | 
|
| t5: | 
|
| t6(m): | 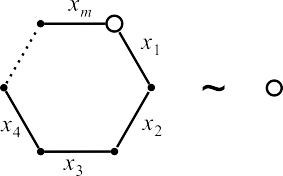
|
[править] Вспомогательные тождества
| t7: | 
|
|---|---|
| t8: | 
|
| t9: | |
| t10: | 
|
| t11: | 
|
[править] По заданной формуле построить подобную ей формулу минимальной глубины.
Определим для ЭК следующие величины:
- ni — число входящих в ЭК переменных
- mi — число входящих в ЭК отрицаний
Тогда hi = ⌈log2(n + m)⌉ — минимальная возможная глубина реализации ЭК.
Раскроем у формулы все скобки и поднимем отрицания, после чего упорядочим в полученной ДНФ элементарные конъюнкции в порядке убывания их высоты. Далее построим каждую ЭК и начнём объединять их в дизъюнкции справа налево. В результате должна получиться СФЭ с минимальной глубиной. Этого делать нельзя, т.к. строится подобная формула.
Итоговая глубина — hfin = ⌈log2(2h1 + … + 2hk))⌉.
[править] Пример
f = x1x2x3x4x5.
- n = 5, m = 2, h = ⌈log2(5 + 2)⌉ = 3
f = ((x1) & (x3)) & ((x2 & x4) & x5)
[править] Пример
f = x1 ∨ x2 ∨ x4x5x6x7x8x9 ∨ x3x7
- x1
- n = 1, m = 1, h = ⌈log2(1 + 1)⌉ = 1
- x2
- n = 1, m = 0, h = ⌈log2(1 + 0)⌉ = 0
- x4x5x6x7x8x9
- n = 6, m = 2, h = ⌈log2(6 + 2)⌉ = 3
- x3x7
- n = 2, m = 2, h = ⌈log2(2 + 2)⌉ = 2
hfinal = ⌈log2(21 + 20 + 23 + 22))⌉ = ⌈log2(15)⌉ = 4
[править] По заданной формуле с поднятыми отрицаниями построить моделирующую ее π-схему и обратно.
Разбираем формулу или схему поэлементно
- A ∨ B эквивалентно ветвлению, где один вариант реализует A, а другой — B
- A & B эквивалентно последовательному соединению, где первая часть реализует A, другая — B.
- xi эквивалентно контакту с меткой xi
- xi эквивалентно контакту с меткой xi
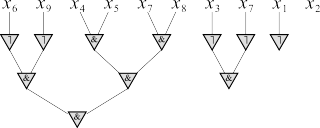
[править] Пример
Решение:
f = x6x9x4x5x7x8 ∨ x3x7 ∨ x1 ∨ x2