МОТП, Контрольная 2013

Материал из eSyr's wiki.

(Различия между версиями)

Текущая версия

Содержание

1 Задача 1
- 1.1 Решение
2 Задача 2
- 2.1 Решение
3 Задача 3
- 3.1 Решение
4 Задача 4
- 4.1 Решение:
5 Задача 5
- 5.1 Решение
6 Задача 6
- 6.1 Решение

[править] Задача 1

Рассматривается задача классификации объектов на два класса по одному признаку. Предполагается, что значение признака x для объектов из классов $K 1$ , $K 2$ распределено по закону Рэлея:

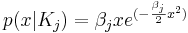
$p(x|K_j) = \beta_j x e^{(-\frac{\beta_j}{2}x^2)}$

Пусть $β 1 = 7.3$ $β 2 = 1.3.$ Требуется найти области значений признака x, соответствующие отнесению объектов в каждый из двух классов байесовским классификатором, если априорные вероятности классов равны, соответственно, 0.3 и 0.7.

[править] Решение

По определению баесовского классификатора:

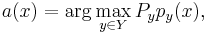
$a(x) = \mathrm{arg}\max_{y\in Y} P_y p_y(x),$

где $x$ - классифицируемый пример, $a (x)$ - классификатор, $Y$ - множество классов ( $K 1, K 2$ ), $P y$ - вероятность появления объекта класса $y$ (априорная вероятность), $p y (x)$ - плотность распределения класса $y$ в точке $x$ .

Построим множество, на котором 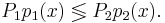$P_1 p_1(x) \lessgtr P_2 p_2(x).$ Для этого решим уравнение:

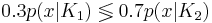
$0.3 p(x|K_1) \lessgtr 0.7 p(x|K_2)$

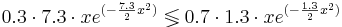
$0.3 \cdot 7.3 \cdot x e^{(-\frac{7.3}{2}x^2)} \lessgtr 0.7 \cdot 1.3 \cdot x e^{(-\frac{1.3}{2}x^2)}$

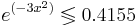
$e^{(-3x^2)} \lessgtr 0.4155$

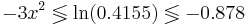
$-3x^2 \lessgtr \ln(0.4155) \lessgtr -0.878$

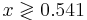
$x \gtrless 0.541$

Таким образом, при $x > 0.541$ классификатор отнесёт объект в класс $K 2$ , при $x < 0.541$ - в класс $K 1$

[править] Задача 2

Имеется задача распознавания с 4-мя классами и одним признаком. Предполагается, что с использованием метода "Линейная машина" для каждого класса найдены следующие линейные разделяющие функции:

$f 1 (x) = 4.8 - 2.3 x$

$f 2 (x) = - 4.6 - 2.6 x$

$f 3 (x) = 4.5 - 2.3 x$

$f 4 (x) = 4.2 - 0.4 x$

Требуется изобразить на графике области, соответствующие отнесению к каждому из четырех классов.

[править] Решение

Для нахождения требуемых областей, решим системы неравенств:

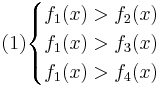
$(1) \begin{cases} f_1(x) > f_2(x) \\ f_1(x) > f_3(x) \\ f_1(x) > f_4(x) \end{cases}$

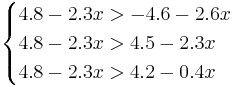
$\begin{cases} 4.8 - 2.3 x > -4.6 - 2.6 x \\ 4.8 - 2.3 x > 4.5 - 2.3 x \\ 4.8 - 2.3 x > 4.2 - 0.4 x \end{cases}$

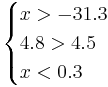
$\begin{cases} x > -31.3 \\ 4.8 > 4.5 \\ x < 0.3 \end{cases}$

Таким образом, объект будет отнесён в класс 1 при 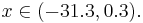$x \in (-31.3, 0.3).$

Аналогично:

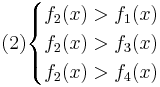
$(2) \begin{cases} f_2(x) > f_1(x) \\ f_2(x) > f_3(x) \\ f_2(x) > f_4(x) \end{cases}$

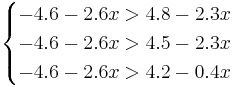
$\begin{cases} -4.6 - 2.6 x > 4.8 - 2.3 x \\ -4.6 - 2.6 x > 4.5 - 2.3 x \\ -4.6 - 2.6 x > 4.2 - 0.4 x \end{cases}$

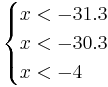
$\begin{cases} x < -31.3 \\ x < -30.3 \\ x < -4 \end{cases}$

Oбъект будет отнесён в класс 2 при 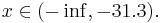$x \in (-\inf, -31.3).$

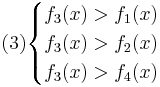
$(3) \begin{cases} f_3(x) > f_1(x) \\ f_3(x) > f_2(x) \\ f_3(x) > f_4(x) \end{cases}$

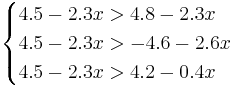
$\begin{cases} 4.5 - 2.3 x > 4.8 - 2.3 x \\ 4.5 - 2.3 x > -4.6 - 2.6 x \\ 4.5 - 2.3 x > 4.2 - 0.4 x \end{cases}$

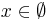$x \in \empty$ , поэтому никакой объект не будет отнесён к классу 3.

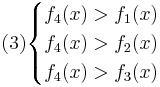
$(3) \begin{cases} f_4(x) > f_1(x) \\ f_4(x) > f_2(x) \\ f_4(x) > f_3(x) \end{cases}$

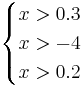
$\begin{cases} x > 0.3 \\ x > -4 \\ x > 0.2 \end{cases}$

Oбъект будет отнесён в класс 4 при 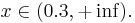$x \in (0.3, +\inf).$

[править] Задача 3

Предполагается, что линейный дискриминант Фишера используется для распознавания объектов из двух классов по паре признаков $x 1$ и $x 2$ . Требуется вычислить вектор, задающий направление перпендикуляра к прямой, разделяющей объекты двух классов:

Класс 1: 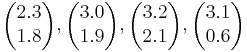$\begin{pmatrix} 2.3 \\ 1.8 \end{pmatrix} , \begin{pmatrix} 3.0 \\ 1.9 \end{pmatrix} , \begin{pmatrix} 3.2 \\ 2.1 \end{pmatrix} , \begin{pmatrix} 3.1 \\ 0.6 \end{pmatrix}$

Класс 2: 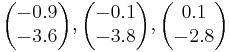$\begin{pmatrix} -0.9 \\ -3.6 \end{pmatrix} , \begin{pmatrix} -0.1 \\ -3.8 \end{pmatrix} , \begin{pmatrix} 0.1 \\ -2.8 \end{pmatrix}$

[править] Решение

Перпендикуляр к прямой, разделяющей объекты двух классов, описывается уравнением:

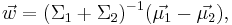
$\vec{w} = ( \Sigma_1 + \Sigma_2 )^{-1}(\vec{\mu_1} - \vec{\mu_2}),$

где 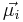$\vec{\mu_i}$ - матожидания объектов каждого класса, а $Σ i$ - ковариационная матрица.

Посчитаем матождиания:

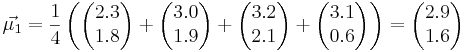
$\vec{\mu_1} = \frac{1}{4} \left( \begin{pmatrix} 2.3 \\ 1.8 \end{pmatrix} + \begin{pmatrix} 3.0 \\ 1.9 \end{pmatrix} + \begin{pmatrix} 3.2 \\ 2.1 \end{pmatrix} + \begin{pmatrix} 3.1 \\ 0.6 \end{pmatrix} \right) = \begin{pmatrix} 2.9 \\ 1.6 \end{pmatrix}$

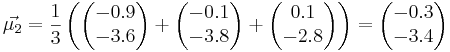
$\vec{\mu_2} = \frac{1}{3} \left( \begin{pmatrix} -0.9 \\ -3.6 \end{pmatrix} + \begin{pmatrix} -0.1 \\ -3.8 \end{pmatrix} + \begin{pmatrix} 0.1 \\ -2.8 \end{pmatrix} \right) = \begin{pmatrix} -0.3 \\ -3.4 \end{pmatrix}$

Посчитаем ковариационные матрицы:

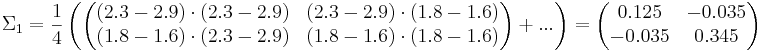
$\Sigma_1 = \frac{1}{4} \left( \begin{pmatrix} (2.3-2.9)\cdot(2.3-2.9) & (2.3 - 2.9)\cdot(1.8 - 1.6)\\ (1.8 - 1.6)\cdot(2.3 - 2.9)& (1.8 - 1.6)\cdot(1.8 - 1.6) \end{pmatrix} + ... \right) = \begin{pmatrix} 0.125& -0.035 \\ -0.035& 0.345 \end{pmatrix}$

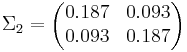
$\Sigma_2 = \begin{pmatrix} 0.187& 0.093 \\ 0.093& 0.187 \end{pmatrix}$

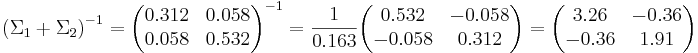
$\left( \Sigma_1 + \Sigma_2 \right)^{-1} = \begin{pmatrix} 0.312& 0.058 \\ 0.058& 0.532 \end{pmatrix}^{-1} = \frac{1}{0.163}\begin{pmatrix} 0.532& -0.058 \\ -0.058& 0.312 \end{pmatrix} = \begin{pmatrix} 3.26& -0.36 \\ -0.36& 1.91 \end{pmatrix}$

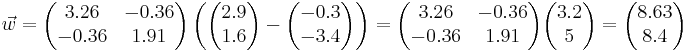
$\vec{w} = \begin{pmatrix} 3.26& -0.36 \\ -0.36& 1.91 \end{pmatrix} \left( \begin{pmatrix} 2.9 \\ 1.6 \end{pmatrix} - \begin{pmatrix} -0.3 \\ -3.4 \end{pmatrix} \right) = \begin{pmatrix} 3.26& -0.36 \\ -0.36& 1.91 \end{pmatrix} \begin{pmatrix} 3.2 \\ 5 \end{pmatrix} = \begin{pmatrix} 8.63 \\ 8.4 \end{pmatrix}$

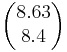
Ответ: $\begin{pmatrix} 8.63 \\ 8.4 \end{pmatrix}$

[править] Задача 4

При проведении выборов на ряде избирательных участков производятся фальсификации результатов голосования. Посылка наблюдателя на такой участок предотвращает фальсификации. Пусть известно несколько точек ROC-кривой для метода идентификации "грязных" участков. Требуется определить оптимальную стратегию распределения наблюдателей по участкам и максимальный выигрыш относительно стратегии равномерного распределения по участкам, если всего участков 1000, наблюдателей --- 200 и доля "грязных" участков --- 30%. При этом под оптимальностью понимается максимизация количества честных участков.

Чувствительность	Ложная тревога
0.86	0.11
0.90	0.31
0.92	0.32

[править] Решение:

Чувствительность - отношение числа верно распознаных примеров позитивного класса к общему размеру класса: 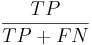$\frac{TP}{TP + FN}$

Ложная тревога - отношение числа ошибочно распознанных примеров позитивного класса к размеру негативного класса: 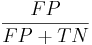$\frac{FP}{FP + TN}$

Позитивный исход - идентификация "грязного" участка.

В случае стратегии равномерного распределения наблюдателей по всем участкам, на выбранном участке будет наблюдатель с вероятностью 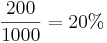$\frac{200}{1000} = 20%$ . Всего чистых участков: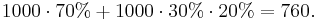 $1000 \cdot 70% + 1000 \cdot 30% \cdot 20% = 760.$

Рассмотрим первый алгоритм.

$300 = T P + F N$

$700 = T N + F P$

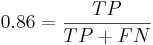
$0.86 = \frac{TP}{TP + FN}$

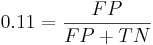
$0.11 = \frac{FP}{FP + TN}$

Решая систему, получаем, что $T P = 258$ , $F P = 77$ , $F N = 42$ , $T N = 623$ . Всего метод возвращает 258+77 = 335 результатов. Наблюдателей в распоряжении - меньше, поэтому распределим их равномерно среди участков, которые вернул метод. Вероятность того, что наблюдатель попадёт на произвольны среди выбранных классификатором участков, равна 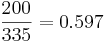$\frac{200}{335} = 0.597$ , поэтому среди выбранных участков наблюдатели попадут в среднем на 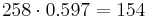$258 \cdot 0.597 = 154$ участка, и всего чистыми будут $700 + 154 = 854$ участка. Выигрыш составил $854 - 760 = 94$ участка.

Аналогично для других точек.

[править] Задача 5

Задана таблица совместных значений прогнозируемой переменной Y и объясняющей переменной X. Требуется вычислить ковариацию между Y и X, коэффициент корреляции между Y и X, коэффициенты одномерной линейной регрессии.

Y	5.9	4.0	2.4	1.7
X	8.3	7.6	3.0	2.3

[править] Решение

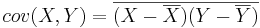
$cov(X,Y) = \overline{(X - \overline{X})(Y - \overline{Y})}$

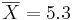
$\overline{X} = 5.3$

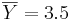
$\overline{Y} = 3.5$

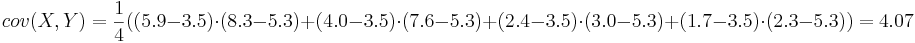
$cov(X,Y) = \frac{1}{4}((5.9 - 3.5)\cdot(8.3 - 5.3) + (4.0 - 3.5)\cdot(7.6 - 5.3) + (2.4 - 3.5)\cdot(3.0 - 5.3) + (1.7 - 3.5)\cdot(2.3 - 5.3)) = 4.07$

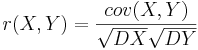
$r(X,Y) = \frac{cov(X,Y)}{\sqrt{DX}\sqrt{DY}}$

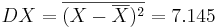
$DX = \overline{(X-\overline{X})^2} = 7.145$

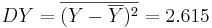
$DY = \overline{(Y-\overline{Y})^2} = 2.615$

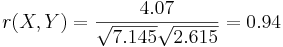
$r(X,Y) = \frac{4.07}{\sqrt{7.145}\sqrt{2.615}} = 0.94$

Воспользуемся методом наименьших квадратов для расчета коэффициентов одномерной линейной регрессии $Y = a + b X$ :

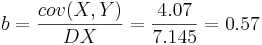
$b = \frac{cov(X,Y)}{DX} = \frac{4.07}{7.145} = 0.57$

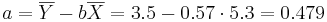
$a = \overline{Y} - b\overline{X} = 3.5 - 0.57 \cdot 5.3 = 0.479$

Получаем линейную регрессию: $Y = 0.479 + 0.57 X$

[править] Задача 6

Заданы таблицы значений бинарных признаков для классов $K 1$ и $K 2$ . Требуется найти все тупиковые тесты минимальной длины, а также указать для каждого класса по одному представительному набору, который не совпадает по признакам с тупиковым тестом.

Класс 1
X_1	X_2	X_3	X_4
0	0	0	0
1	0	1	0
0	0	0	1

Класс 2
X_1	X_2	X_3	X_4
1	0	1	1
1	1	0	0
1	1	0	0

[править] Решение

Кратчайший тупиковый тест состоит из трёх столбцов: $(X 1, X 2, X 4),(X 1, X 3, X 4)$ или $(X 2, X 3, X 4)$ . Тестов длины 2 не существует, т.к. для любой пары столбцов найдутся две одинаковые строки в каждой из таблиц.

Представительный набор определяется для класса и для элемента. Например, для первого элемента первого класса представительным будет набор - $(0,0, X 3, X 4)$ (заметим, что этот набор не тупиковый, подходит также $(0, X 2, X 3, X 4)$ ), а для первого элемента второго класса - набор $(X 1, X 2,1,1)$

Математические основы теории прогнозирования

Материалы по курсу
Билеты (2009) | Примеры задач (2009) | Примеры задач контрольной работы (2013) | Определения из теории вероятностей

Получено с http://esyr.org/wiki/%D0%9C%D0%9E%D0%A2%D0%9F%2C_%D0%9A%D0%BE%D0%BD%D1%82%D1%80%D0%BE%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_2013

@@ Строка 11: / Строка 11: @@
 По определению [http://machinelearning.ru/wiki/index.php?title=%D0%91%D0%B0%D0%B9%D0%B5%D1%81%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%BA%D0%BB%D0%B0%D1%81%D1%81%D0%B8%D1%84%D0%B8%D0%BA%D0%B0%D1%82%D0%BE%D1%80 баесовского классификатора]:
-<math>a(x) = \mathrm{arg}\max_{y\in Y} \lambda_{y} P_y p_y(x),</math>
+<math>a(x) = \mathrm{arg}\max_{y\in Y} P_y p_y(x),</math>
-где <math>x</math> - классифицируемый пример, <math>a(x)</math> - классификатор, <math>Y</math> - множество классов (<math>K_1, K_2</math>), <math>\lambda_y</math> - цена ошибки (<math>\lambda_1 = \lambda_2</math>), <math>P_y</math> - вероятность появления объекта класса <math>y</math> (априорная вероятность), <math>p_y(x)</math> - плотность распределения класса <math>y</math> в точке <math>x</math>.
+где <math>x</math> - классифицируемый пример, <math>a(x)</math> - классификатор, <math>Y</math> - множество классов (<math>K_1, K_2</math>), <math>P_y</math> - вероятность появления объекта класса <math>y</math> (априорная вероятность), <math>p_y(x)</math> - плотность распределения класса <math>y</math> в точке <math>x</math>.
-Построим множество, на котором <math> \lambda_{1} P_1 p_1(x) \lessgtr \lambda_{2} P_2 p_2(x).</math> Для этого решим уравнение:
+Построим множество, на котором <math> P_1 p_1(x) \lessgtr P_2 p_2(x).</math> Для этого решим уравнение:
-<math> \lambda_{1} 0.3 p(x|K_1) \lessgtr \lambda_{2} 0.7 p(x|K_2) </math>
+<math> 0.3 p(x|K_1) \lessgtr 0.7 p(x|K_2) </math>
 <math> 0.3 \cdot 7.3 \cdot x e^{(-\frac{7.3}{2}x^2)} \lessgtr 0.7 \cdot 1.3 \cdot x e^{(-\frac{1.3}{2}x^2)} </math>
@@ Строка 215: / Строка 215: @@
 <math> 0.11 = \frac{FP}{FP + TN} </math>
-Решая систему, получаем, что <math> TP = 258 </math>, <math> FP = 77 </math>, <math> FN = 42 </math>, <math> TN = 623 </math>
+Решая систему, получаем, что <math> TP = 258 </math>, <math> FP = 77 </math>, <math> FN = 42 </math>, <math> TN = 623 </math>. Всего метод возвращает 258+77 = 335 результатов. Наблюдателей в распоряжении - меньше, поэтому распределим их равномерно среди участков, которые вернул метод. Вероятность того, что наблюдатель попадёт на произвольны среди выбранных классификатором участков, равна <math> \frac{200}{335} = 0.597 </math>, поэтому среди выбранных участков наблюдатели попадут в среднем на <math> 258 \cdot 0.597 = 154 </math> участка, и всего чистыми будут <math> 700 + 154 = 854</math> участка. Выигрыш составил <math>854-760 = 94</math> участка.
+Аналогично для других точек.
+== Задача 5 ==
+Задана таблица совместных значений прогнозируемой переменной Y и объясняющей переменной X. Требуется вычислить ковариацию между Y и X, коэффициент корреляции между Y и X, коэффициенты одномерной линейной регрессии.
+{| border = 1
+ | Y
+ | 5.9
+ | 4.0
+ | 2.4
+ | 1.7
+ |-
+ | X
+ | 8.3
+ | 7.6
+ | 3.0
+ | 2.3
+ |}
+=== Решение ===
+<math> cov(X,Y) = \overline{(X - \overline{X})(Y - \overline{Y})} </math>
+<math> \overline{X} = 5.3 </math>
+<math> \overline{Y} = 3.5 </math>
+<math> cov(X,Y) = \frac{1}{4}((5.9 - 3.5)\cdot(8.3 - 5.3) + (4.0 - 3.5)\cdot(7.6 - 5.3) + (2.4 - 3.5)\cdot(3.0 - 5.3) + (1.7 - 3.5)\cdot(2.3 - 5.3)) = 4.07 </math>
+<math> r(X,Y) = \frac{cov(X,Y)}{\sqrt{DX}\sqrt{DY}} </math>
+<math> DX = \overline{(X-\overline{X})^2} = 7.145 </math>
+<math> DY = \overline{(Y-\overline{Y})^2} = 2.615 </math>
+<math> r(X,Y) = \frac{4.07}{\sqrt{7.145}\sqrt{2.615}} = 0.94 </math>
+Воспользуемся методом наименьших квадратов для расчета коэффициентов одномерной линейной регрессии <math> Y = a + bX </math>:
+<math> b = \frac{cov(X,Y)}{DX} = \frac{4.07}{7.145} = 0.57 </math>
+<math> a =  \overline{Y} - b\overline{X} = 3.5 - 0.57 \cdot 5.3 = 0.479 </math>
+Получаем линейную регрессию: <math> Y = 0.479 + 0.57X </math>
+== Задача 6 ==
+Заданы таблицы значений бинарных признаков для классов <math>K_1</math> и <math>K_2</math>. Требуется найти все тупиковые тесты минимальной длины, а также указать для каждого класса по одному представительному набору, который не совпадает по признакам с тупиковым тестом.
+{| border = 1
+ |colspan="4" | Класс 1
+ |-
+ | X_1 || X_2 || X_3 || X_4
+ |-
+ | 0 || 0 || 0 || 0
+ |-
+ | 1 || 0 || 1 || 0
+ |-
+ | 0 || 0 || 0 || 1
+ |}
+ {| border = 1
+ |colspan="4" | Класс 2
+ |-
+ | X_1 || X_2 || X_3 || X_4
+ |-
+ | 1 || 0 || 1 || 1
+ |-
+ | 1 || 1 || 0 || 0
+ |-
+ | 1 || 1 || 0 || 0
+ |}
+=== Решение ===
+Кратчайший тупиковый тест состоит из трёх столбцов: <math> (X_1, X_2, X_4), (X_1, X_3, X_4) </math> или <math> (X_2, X_3, X_4) </math>. Тестов длины 2 не существует, т.к. для любой пары столбцов найдутся две одинаковые строки в каждой из таблиц.
+Представительный набор определяется для класса и для элемента. Например, для первого элемента первого класса представительным будет набор - <math>(0, 0, X_3, X_4)</math> (заметим, что этот набор не тупиковый, подходит также <math>(0, X_2, X_3, X_4)</math>), а для первого элемента второго класса - набор <math>(X_1, X_2, 1, 1)</math>
 {{Курс МОТП}}

МОТП, Контрольная 2013

Материал из eSyr's wiki.

Текущая версия

Содержание

[править] Задача 1

[править] Решение

[править] Задача 2

[править] Решение

[править] Задача 3

[править] Решение

[править] Задача 4

[править] Решение:

[править] Задача 5

[править] Решение

[править] Задача 6

[править] Решение

Просмотры

Личные инструменты

Навигация

инструменты

Разделы

Спецкурсы

9 семестр

7 семестр

5 семестр

3 семестр

Поиск

Инструменты