МОТП, Билеты (2009)

Материал из eSyr's wiki.

(Различия между версиями)

Перейти к: навигация, поиск

Версия 11:05, 26 мая 2009

Содержание

1 Часть 1 (Ветров)
2 Часть 2 (Рудаков)

Часть 1 (Ветров)

Метод максимального правдоподобия. Его достоинства и недостатки.

Недостатки:

нужно знать априорное распределение (с точностью до параметров) наблюдаемой величины
хорошо применим при допущении, что 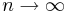$n \rightarrow \infty$ (асимптотически оптимален), что в реальности не так
проблема выбора структурных параметров, позволяющих избегать переобучения (проблема вообще всех методов машинного обучения)
необходима регуляризация метода

Решение несовместных СЛАУ.

В статистике, машинном обучении и теории обратных задач под регуляризацией понимают добавление некоторой дополнительной информации к условию с целью решить некорректно поставленную задачу или предотвратить переобучение.

Несовместная СЛАУ -- система линейных уравнений, не имеющая ни одного решения.

Совместная СЛАУ -- система линейных уравнений, имеющая хотя бы одно решение.

Ридж-регуляризация (ридж-регрессия, регуляризация Тихонова) матрицы $A T A$ -- матрица $A T A + λ I$ , где $λ$ -- коэффициент регуляризации. Всегда невырождена при $λ > 0$

Нормальное псевдорешение СЛАУ $A x = b$ -- вектор $x = (A T A + λ I) - 1 A T b$

всегда единственно
при небольших $λ$ определяет псевдорешение с наименьшей нормой
любое псевдорешение имеет минимальную невязку

Задача восстановления линейной регрессии. Метод наименьших квадратов.

Задача регрессионного анализа (неформально): Предположим имеется зависимость между наблюдаемыми признаками (случайной выборкой) X и некоторой переменной (параметром) t. Задача регрессионного анализа -- определение наличия и характера (математического уравнения, описывающего зависимость) связи между переменными

Пример: простой пример на пальцах: Linear Regression Example

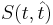$S(t, \hat{t})$ -- функция потерь от ошибки. На пальцах: берем найденную путем регрессии функцию 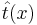$\hat{t}(x)$ и сравниваем её выдачу на тех же наборах $x$ , что и заданные результаты эксперимента $t (x)$ .

$S_1(t, \hat{t}) = (t - \hat{t})^2$
$S_2(t, \hat{t}) = |t - \hat{t}|^2$
$S_3(t, \hat{t}) = \delta^{-1}(t - \hat{t})$

Основная задача -- минимизировать эту функцию, что значит минимизировать 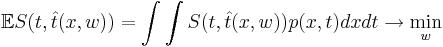$\mathbb{E} S(t, \hat{t}(x,w)) = \int\int S(t, \hat{t}(x,w)) p(x,t) dx dt \rightarrow \min_{w}$

Метод наименьших квадратов -- минимизация функции потери ошибки 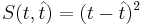$S(t, \hat{t}) = (t - \hat{t})^2$

Особенности квадратичной функции потерь:

Достоинтсва
- гладкая (непрерывная и дифференцируемая)
- решение может быть получено в явном виде
Недостатки
- решение неустойчиво
- не применима к задачам классификации

Задача восстановления линейной регрессии. Вероятностная поставновка.

Представим регрессионную переменную как случайную величину с плотностью распределения $p (t | x)$

В большинстве случаев предполагается нормальное распределение относительно некоторой точки y(x) : 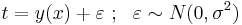$t = y(x) + \varepsilon~;~~\varepsilon \sim N(0, \sigma^2)$

[?]: почему в лекциях (лекция 1, слайд 22): 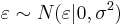$\varepsilon \sim N(\varepsilon | 0, \sigma^2)$ Как я понимаю 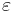$\varepsilon$ -- это произвольный параметр, мы просто предполагаем, что он распределен нормально.

максимизируя правдоподобие получаем эквивалентность данного метода методу наименьших квадратов

Логистическая регрессия. Вероятностная постановка.

ЕМ-алгоритм для задачи разделения гауссовской смеси.

Основные правила работы с вероятностями. Условная независимость случайных величин.

Графические модели. Основные задачи, возникающие в анализе графических моделей.

Байесовские сети. Примеры.

На википедии

Марковские сети. Примеры.

Скрытые марковские модели. Обучение СММ с учителем.

На википедии

Викибуки

Алгоритм динамического программирования и его применение в скрытых марковских моделях.

ЕМ-алгоритм и его применение в скрытых марковских моделях.

Условная независимость в скрытых марковских моделях. Алгоритм «вперед-назад».

Метод релевантных векторов в задаче восстановления регрессии.

Метод релевантных векторов в задаче классификации.

Метод главных компонент.

Пусть имеется некоторая выборка 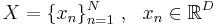$X = \{x_n\}_{n=1}^N~,~~ x_n \in \mathbb{R}^D$ . Цель -- представить выборку в пространстве меньшей размерности $d < D$ таким образом, чтобы в новом пространстве "схожие" объекты образовывали компактные области.

PCA (Principal Component Analysis) -- Метод главных компонент. Формулировки:

проекция данных на гиперплоскость с наименьшей ошибкой проектирования
поиск проекции на гиперплоскость с сохранением большей части дисперсии в данных

Вероятностная формулировка метода главных компонент.

ЕМ-алгоритм в методе главных компонент. Его преимущества.

Метод главных компонент. Схема автоматического выбора числа главных компонент.

Недостатки метода главных компонент. Метод независимых компонент.

Нелинейные методы уменьшения размерности. Локальное линейное погружение.

Нелинейные методы уменьшения размерности. Ассоциативные нейронные сети и GTM.

Часть 2 (Рудаков)

Объекты, признаки, логические признаки, простейшие логические решающие правила.

Признаки объектов:

детерминированные;
вероятностные;
логические;
структурные.

Детерминированные признаки – это признаки, принимающие конкретные числовые значения, которые могут быть рассмотрены как координаты точки, соответствующей данному объекту, в n-мерном пространстве признаков.

Вероятностные признаки – это признаки, случайные значения которых распределены по всем классам объектов, при этом решение о принадлежности распознаваемого объекта к тому или другому классу может приниматься только на основании конкретных значений признаков данного объекта, определенных в результате проведения соответствующих опытов. Признаки распознаваемых объектов следует рассматривать как вероятностные и в случае, если измерение их числовых значений производится с такими ошибками, что по результатам измерний невозможно с полной определенностью сказать, какое числовое значение данная величина приняла.

Логические признаки распознаваемых объектов можно рассматривать как элементарные высказывания, принимающие два значения истинности (истина – ложь) с полной определенностью. К логическим признакам относятся прежде всего признаки, не имеющие количественного выражения. Эти признаки представляют собой суждения качественного характера типа наличия или отсутствия некоторых свойств или некоторых элементов у распознаваемых объектов или явлений. В качестве логических признаков можно рассматривать, например, такие симптомы в медицинской диагностике, как боль в горле, кашель и т.д. К логическим можно отнести также признаки, у которых важна не величина признака у распознаваемого объекта, а лишь факт попадания или непопадания ее в заданный интервал. В пределах этих интервалов появление различных значений признаков у распознаваемых объектов предполагается равновероятным. На практике логические признаки подобного рода имеют место в таких ситуациях, когда либо ошибками измерений можно пренебречь, либо интервалы значений признаков выбраны таким образом, что ошибки измерений практически не оказывают влияния на достоверность принимаемых решений относительно попадания измеряемой величины в заданный интервал.

Проблемы формирования логических признаков. Оценки качества признаков и их совокупностей.

Пусть 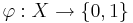$\varphi : X \rightarrow \{0, 1\}$ - некоторый предикат, определённый на множестве объектов X. Говорят, что предикат 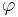$\varphi$ выделяет или покрывает (cover) объект x, если 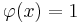$\varphi(x) = 1$ . Предикат называют закономерностью, если он выделяет достаточно много объектов какого-то одного класса $c$ , и практически не выделяет объекты других классов.

Пример: Решается вопрос о целесообразности хирургической операции. Закономерность: если возраст пациента выше 60 лет и ранее он перенёс инфаркт, то операцию не делать - риск отрицательного исхода велик.

Всякая закономерность классифицирует лишь некоторую часть объектов. Объединив определённое количество закономерностей в композицию, можно получить алгоритм, способный классифицировать любые объекты. Логическими алгоритмами классификации будем называть композиции легко интерпретируемых закономерностей. При построении логических алгоритмов возникают три основных вопроса:

Каков критерий информативности, позволяющий называть предикаты закономерностями?
Как строить закономерности?
Как строить алгоритмы классификации на основе закономерностей? Наиболее распространённые типы логических алгоритмов: Алгоритм Кора (голосование), Алгоритмы вычисления оценок.

Теперь поговорим об информативности (или качестве) признака. Своими словами: предикат \varphi тем более информативен, чем больше он выделяет объектов "своего класса" 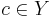$c \in Y$ по сравнению с объектами всех остальных "чужих" классов. Свои объекты называют также позитивными (positive), а чужие негативными (negative). Введём следующие обозначения:

$P c$ - число объектов класса c в выборке X
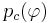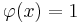$p_c(\varphi)$ - из них число объектов, для которых выполняется условие $\varphi(x) = 1$ ;
$N c$ - число объектов всех остальных классов Y \ {c} в выборке X
$n_c(\varphi)$ - из них число объектов, для которых выполняется условие $\varphi(x) = 1$

Введем ещё два обозначения:

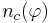$E_c ( \varphi , X ) = \frac {n_c(\varphi)}{p_c(\varphi)+ n_c(\varphi)}$ - доля негативных среди всех выделяемых объектов (доля тех объектов, в которых наш логический предикат ошибся - причислил их к "своему" классу, хотя они туда и не относились)
$D_c ( \varphi , X ) = \frac {p_c(\varphi)}{l}$ , где l - это количество элементов в выборке X. Доля выделенных позитивных объектов.

Существует несколько способов определения информативности: статическое определение, энтропийное. Также существует такое понятие как многоклассовая информативность, когда приходится оценивать информативность не только таких предикатов, которые отделяют один класс от остальных, но и таких, которые отделяют некоторую группу классов от остальных.

Методы голосования по конъюнкциям. Алгоритмы типа "Кора".

Тесты, представительные наборы, проблемы перебора.

Пространства объектов для АВО. Обучающие и контрольные объекты. Метрические описания объектов в АВО.

Опорные множества в АВО. Функции близости. Веса объектов и признаков.

Формулы вычисления оценок. Эвристические обоснования.

Задачи оптимизации АВО. Совместные подсистемы систем неравенств.

Функционалы качества. Сложность моделей алгоритмов и проблема переобучения.

Общие пространства начальных и финальных информаций. Задачи синтеза корректных алгоритмов.

Разрешимость и регулярность задач распознавания. Регулярность по Ю.И. Журавлёву

Операции над алгоритмами. Расширение моделей.

Пространства оценок. Алгоритмы как суперпозиции.

Понятие полноты моделей алгоритмов и семейств корректирующих операций.

Дополнительные к прецедентам ограничения. Пример: перестановочность строк и столбцов в матрицах информации.

Задачи с непересекающимися классами.

Класс поэлементных операций и отображений. Условия регулярности и полноты.

Полнота моделей АВО.

Полнота полиномиальных семейств корректирующих операций.

Логарифмическая граница степени корректирующих полиномов.

Проблема построения набора базовых операторов для конкретных задач. Дефекты различимости и монотонности. Сходимость методов синтеза мультиалгоритмических конструкций.

Получено с http://esyr.org/wiki/%D0%9C%D0%9E%D0%A2%D0%9F%2C_%D0%91%D0%B8%D0%BB%D0%B5%D1%82%D1%8B_%282009%29

@@ Строка 114: / Строка 114: @@
 == Проблемы формирования логических признаков. Оценки качества признаков и их совокупностей. ==
-Задача '''оценки информативности признаков''' и объектов состоит в вычислении относительного вклада признака (объекта) в процесс распознавания.
+Пусть <math>\varphi : X \rightarrow \{0, 1\}</math> - некоторый предикат, определённый на множестве объектов X. Говорят, что предикат <math>\varphi</math> ''выделяет'' или ''покрывает'' (cover) объект x, если
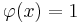
+<math>\varphi(x) = 1</math>. Предикат называют ''закономерностью'', если он выделяет достаточно много объектов какого-то одного класса <math>c</math>, и практически не выделяет объекты других классов.
-Для начала, введем понятие '''функционал качества''' алгоритма.
+Пример: Решается вопрос о целесообразности хирургической операции. Закономерность: если возраст пациента выше 60 лет и ранее он перенёс инфаркт, то операцию не делать - риск отрицательного исхода велик.
-Пусть задана таблица контрольных объектов (множество объектов, на которых мы будет проверять качество работы нашего алгоритма распознавания). Для контрольных объектов мы должны знать, как какому классу свойств относится каждый из объектов (иначе как мы будет проверять корректность работы нашего алгоритма). Подаем контрольные объекты на вход алгоритму. Доля правильных ответов, выданных алгоритмов - это и есть ''функционал качества''.
-Введем следующие обозначения
+Всякая закономерность классифицирует лишь некоторую часть объектов. Объединив определённое количество закономерностей в композицию, можно получить
-* <math>\varphi (A)</math> - функционал качества алгоритма A.
+алгоритм, способный классифицировать любые объекты. ''Логическими алгоритмами классификации'' будем называть композиции легко интерпретируемых закономерностей. При построении логических алгоритмов возникают три основных вопроса:
-* <math>\varphi (A^i)</math> - функционал качества алгоритма A, построенного по данным обучения без учета i-го признака
+* Каков критерий информативности, позволяющий называть предикаты закономерностями?
+* Как строить закономерности?
+* Как строить алгоритмы классификации на основе закономерностей? Наиболее распространённые типы логических алгоритмов: Алгоритм Кора (голосование), Алгоритмы вычисления оценок.
-'''Мерой информативности (весом) признака''' называется величина <math>p_i = \frac {\varphi(A) - \varphi (A^i)}{\varphi(A)}</math>
+Теперь поговорим об '''информативности''' (или качестве) признака.
+Своими словами: предикат \varphi тем более информативен, чем больше он выделяет объектов "своего класса" <math>c \in Y</math> по сравнению с объектами всех остальных "чужих" классов. Свои объекты называют также ''позитивными'' (positive), а чужие ''негативными'' (negative). Введём следующие обозначения:
+* <math>P_c</math> - число объектов класса c в выборке X
+* <math>p_c(\varphi)</math> - из них число объектов, для которых выполняется условие <math>\varphi(x) = 1</math>;
+* <math>N_c</math> - число объектов всех остальных классов Y \ {c} в выборке X
+* <math>n_c(\varphi)</math> - из них число объектов, для которых выполняется условие <math>\varphi(x) = 1</math>
-Аналогично - для совокупности признаков.
+Введем ещё два обозначения:
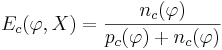+*  <math>E_c ( \varphi , X ) = \frac {n_c(\varphi)}{p_c(\varphi)+ n_c(\varphi)}</math> - доля негативных среди всех выделяемых объектов (доля тех объектов, в которых наш логический предикат ошибся - причислил их к "своему" классу, хотя они туда и не относились)
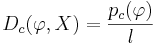+* <math>D_c ( \varphi , X ) = \frac {p_c(\varphi)}{l}</math>, где l - это количество элементов в выборке X. Доля выделенных позитивных объектов.
+Существует несколько способов определения информативности: статическое определение, энтропийное. Также существует такое понятие как ''многоклассовая информативность'', когда приходится оценивать информативность не только таких предикатов, которые отделяют один класс от остальных, но и таких, которые отделяют некоторую группу классов от остальных.
 == Методы голосования по конъюнкциям. Алгоритмы типа "Кора". ==