Определения из теории вероятностей
Материал из eSyr's wiki.
(→Вероятность) |
(→Вероятность) |
||
| Строка 24: | Строка 24: | ||
'''Вероятность''' - мера, заданная на измеримом пространстве (Ω, X): | '''Вероятность''' - мера, заданная на измеримом пространстве (Ω, X): | ||
| - | * | + | * Р(Ω)=1 |
| - | * | + | * Р(А)>=0 для любого <math>А \in X</math>; |
* обладает свойством сигма-аддитивности (счетной аддитивности) . | * обладает свойством сигма-аддитивности (счетной аддитивности) . | ||
Версия 16:17, 24 мая 2009
Содержание |
σ-алгебра
Совокупность A подмножеств множества Ω называется σ-алгеброй:
-
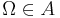
-
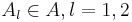 , то
, то 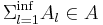
- если
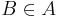 , то
, то 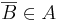
Случайный эксперимент
Случайный эксперимент -- это математическая модель соответствующего реального эксперимента, результат которого невозможно точно предсказать.
Случайная величина
Случайная величина -- подмножество исходов случайного эксперимента. При многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.
Случайная величина — это измеримая функция, заданная на каком-либо вероятностном пространстве.
Определение
Пусть 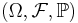 — вероятностное пространство. Функция
— вероятностное пространство. Функция 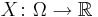 , измеримаяотносительно
, измеримаяотносительно 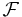 и борелевской σ-алгебры на
и борелевской σ-алгебры на 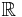 , называется случайной величиной.
, называется случайной величиной.
Вероятностное поведение случайной величины полностью описывается её распределением.
Вероятность
Вероятность (вероятностная мера) — мера достоверности случайного события. Оценкой вероятности события может служить частота его наступления в длительной серии независимых повторений случайного эксперимента]. Согласно определению П. Лапласа мерой вероятности называется дробь, числитель которой есть число всех благоприятных случаев, а знаменатель - число всех возможных случаев.
Вероятность - мера, заданная на измеримом пространстве (Ω, X):
- Р(Ω)=1
- Р(А)>=0 для любого Невозможно разобрать выражение (неизвестная ошибка): А \in X
- обладает свойством сигма-аддитивности (счетной аддитивности) .
Вероятностное пространство
Определение
Вероятностное пространство — это тройка 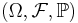 , где
, где
-
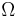 — это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;
— это произвольное множество, элементы которого называются элементарными событиями, исходами или точками;
-
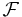 — сигма-алгебра подмножеств
— сигма-алгебра подмножеств 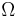 , называемых (случайными) событиями;
, называемых (случайными) событиями;
-
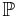 — вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что
— вероятностная мера или вероятность, т.е. сигма-аддитивная конечная мера, такая что 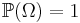 .
.
Замечания
- Элементарные события (элементы
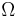 ), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.
), по определению, — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один.
- Каждое случайное событие (элемент
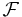 ) — это подмножество
) — это подмножество 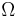 . Говорят, что в результате эксперимента произошло случайное событие
. Говорят, что в результате эксперимента произошло случайное событие 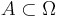 , если (элементарный) исход эксперимента является элементом A.
, если (элементарный) исход эксперимента является элементом A.
Требование, что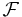 является сигма-алгеброй подмножеств
является сигма-алгеброй подмножеств 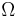 , позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.
, позволяет, в частности, говорить о вероятности случайного события, являющегося объединением счетного числа случайных событий, а также о вероятности дополнения любого события.
Распределение вероятностей
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.
Определение
Определение Пусть задано вероятностное пространство 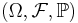 , и на нём определена случайная величина
, и на нём определена случайная величина 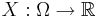 . В частности, по определению, X является измеримым отображением измеримого пространства
. В частности, по определению, X является измеримым отображением измеримого пространства 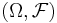 в измеримое пространство
в измеримое пространство 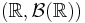 , где
, где 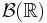 обозначает борелевскую сигма-алгебру на
обозначает борелевскую сигма-алгебру на 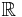 . Тогда случайная величина X индуцирует вероятностную меру
. Тогда случайная величина X индуцирует вероятностную меру 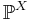 на
на 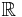 следующим образом:
следующим образом:
Мера 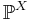 называется распределением случайной величины X.
называется распределением случайной величины X.