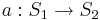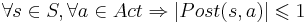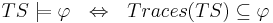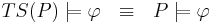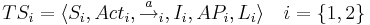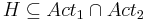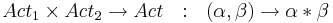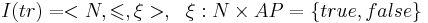ВПнМ/Теормин

Материал из eSyr's wiki.

(Различия между версиями)

Версия 12:34, 20 мая 2009

Содержание

1 Лекция 1
2 Моделирование и абстракция

Лекция 1

Валидация - исследование и обоснование того, что спецификация ПО и само ПО через реализованную в нём функциональность удовлетворяет ребованиям пользователей.

Верификация - исследование и обоснование того, что программа соответствует своей спецификации.

Верификация в общем случае алгоритмически неразрешима.

Методы верификации:

"Полное" тестирование (слайды 14-22)
Имитационное моделирование
Доказательство теорем (27-29)
Статический анализ (30-33)
Верификация на моделях (34-38)

Моделирование и абстракция

Моделирование программ. Понятие состояния. Потенциальные и достижимые состояния. Требования к модели. Процесс построения модели.

Схема верификации на моделях (Лекция 2, слайд 3)

Состояние программы - совокупность значений переменных и управления, связанных с некоторой моделью программы.

Модель - упрощённое описание реальности, выполненное с определенной целью.

с каждым объектом может быть связано несколько моделей
каждая модель отражает свой аспект реальности

Аспекты модели:

простота - модель должна быть проще, чем реальность
корректность - не расходиться с реальностью
адекватность - соответствовать решаемой задаче

Построение модели

формализация требований (постановка задачи моделирования)
выбор языка моделирования
абстракция системы до модели с учётом требований

Моделирование программ. Размеченные системы переходов. Детерминизм и недетерминизм. Вычисления и трассы. Свойства линейного времени. Выполнимость свойства на трассе.

Размеченная система переходов (LTS)

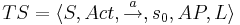
$TS = \langle S, Act, \overset{a}{\rightarrow} ,s_0, AP, L \rangle$

S - множество состояний
Act - множество действий
$τ$ - невидимое действие
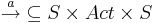$\overset{a}{\rightarrow} \subseteq S \times Act \times S$ - тотальное отношение переходов
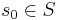$s_0 \in S$ - начальное состояние
AP - множество атомарных высказываний
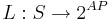$L:S \rightarrow 2^{AP}$ - функция разметки

S, Act - конечные или счётные множества

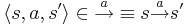
$\langle s, a, s' \rangle \in \overset{a}{\rightarrow} \equiv s \overset{a}{\rightarrow} s'$

Пример LTS: Лекция 2, слайд 40-41

Прямые потомки

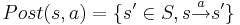$Post(s, a) = \{s' \in S, s \overset{a}{\rightarrow} s'\}$ - такие состояния s', которые непосредственно вытекают из s через переход a
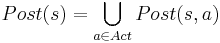$Post(s) = \bigcup_{a \in Act} Post(s, a)$ - все возможные состояния s', которые непосредственно вытекают из s

Система 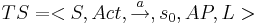$TS = <S, Act, \overset{a}{\rightarrow} ,s_0, AP, L>$ детерменирована:

по действиям тогда и только тогда, когда
- $|I| \leqslant 1$
- $\forall s \in S, \forall a \in Act \Rightarrow |Post(s, a)| \leqslant 1$
по атомарным высказываниям
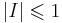
- $|I| \leqslant 1$
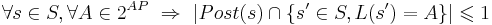- $\forall s \in S, \forall A \in 2^{AP} ~ \Rightarrow ~ |Post(s) \cap \{s' \in S, L(s') = A\}| \leqslant 1$ ( количество одинаково размеченных потомков не больше одного )

Недетерменизм - это фича! Полезен для:

моделирования параллельного выполнения в режиме чередования (интерливинга)
- позволяет не указывать скорость выполнения процессов
моделирования прототипа системы
- не ограничивает реализацию заданным порядком выполнения операторов
построения абстракции реальной системы
- модель может быть построена по неполной информации

Вычисления

Конечный фрагмент вычисления $σ$ системы переходов TS называется конечная последовательность чередующихся состояний и действий $\sigma = s_0 a_1 s_1 a_2 s_2 \dots a_n s_n, \forall i \in [0,n] \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}$
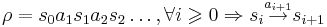
Бесконечный (максимальный) фрагмент вычисления $ρ$ - $\rho = s_0 a_1 s_1 a_2 s_2 \dots, \forall i \geqslant 0 \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}$
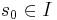
Начальный фрагмент вычисления - фрагмент вычисления, для которого $s_0 \in I$
Вычисление - начальный максимальный фрагмент вычисления

Достижимое состояние (из начального) в системе переходов TS - такое состояние 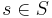$s \in S$ , для которого существует конечный фрагмент вычисления $s_0 a_1 s_1 a_2 s_2 \dots a_n s_n = s$

Rich(TS) - множество всех достижимых состояний в TS

Трасса 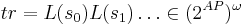$tr = L(s_0) L(s_1) \dots \in (2^{AP})^\omega$

Свойства линейного времени

Свойство 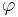$\varphi$ определяет набор допустимых трасс: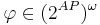 $\varphi \in (2^{AP})^\omega$
Система переходов TS удовлетворяет свойству линейного времени
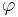
- $TS \models \varphi ~~ \Leftrightarrow ~~ Traces(TS) \subseteq \varphi$
- $TS(P) \models \varphi ~~ \equiv ~~ P \models \varphi$

Моделирование программ. Графы программ. Статическая и операционная семантика.

Граф программы – формальное описание текста программы.

$D p$ -- единый абстрактный домен данных.
P -- программа.
- $V p$ -- множество переменных программы(Var).
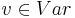
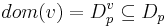- $dom(v) = D_p^v \subseteq D_p$ -- каждая переменная принадлежит какому-либо домену
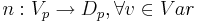
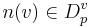
$n$ -- подстановка. $n: V_p \rightarrow D_p, \forall v \in Var$ $n(v) \in D_p^v$
Cond(V_p) -- Набор булевых условий над V_p
- формулы пропозициональной логики
- условия на переменные
Эффект операторов:

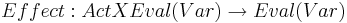
$Effect: Act X Eval(Var) \rightarrow Eval(Var)$

Граф программы:

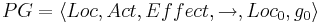
$PG= \langle Loc , Act , Effect ,\rightarrow, Loc_0, g_0 \rangle$

$L o c$ -- множество точек, 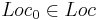$Loc_0 \in Loc$ -- множество начальных точек
$A c t$ -- множество действий
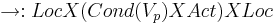$\rightarrow : Loc X (Cond(V_p) X Act) X Loc$ -- отношение перехода
$E f f e c t$ -- функция эффекта
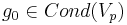$g_0 \in Cond(V_p)$ -- начальное условие

Системы переходов графов программ TS(PG) -- система переходов графа программы 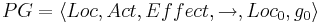$PG= \langle Loc , Act , Effect ,\rightarrow, Loc_0, g_0 \rangle$ задается сигнатурой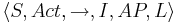 $\langle S, Act, \rightarrow, I, AP, L \rangle$

$S = L o c X E v a l (V p)$

Параллелизм. Чередование систем переходов.

Параллелизм. Чередование графов программ. Случаи без разделяемых переменных и с разделяемыми переменными.

Параллелизм. Синхронный параллелизм. Рандеву.

распределённые программы выполняются параллельно
в распределённой программе нет разделяемых переменных

Передача сообщений в распределённых программах:

cинхронная передача сообщений (рандеву)
асинхронная передача сообщений (кналы)

Синхронный обмен сообщенийями:

Процессы вместе выполняют синхронизированные действия
Взаимодействие процессов - одновременно

Рандеву

$TS_i = \langle S_i, Act_i, \overset{a}{\rightarrow}_i ,I_i, AP_i, L_i \rangle ~~~ i=\{1,2\}$
$H \subseteq Act_1 \cap Act_2$

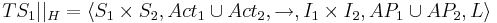Тогда $TS_1 ||_H = \langle S_1 \times S_2, Act_1 \cup Act_2, \rightarrow, I_1 \times I_2, AP_1 \cup AP_2, L \rangle$ , где

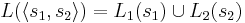
$L(\langle s_1, s_2 \rangle) = L_1(s_1) \cup L_2(s_2)$
определяется как:
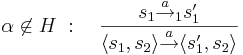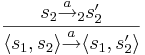
- интерливинг для $\alpha \not\in H~:~~~ \frac{s_1 \overset{a}{\rightarrow}_1 s_1'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1', s_2 \rangle}$ и $\frac{s_2 \overset{a}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1, s_2' \rangle}$
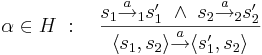
- рандеву для $\alpha \in H~:~~~ \frac{s_1 \overset{a}{\rightarrow}_1 s_1' ~ \wedge ~ s_2 \overset{a}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1', s_2 \rangle}$

Пример рандеву: Лекция 4, слайд 32

Синхронный параллелизм

$TS_i = \langle S_i, Act_i, \overset{a}{\rightarrow}_i ,I_i, AP_i, L_i \rangle ~~~ i=\{1,2\}$
$Act_1 \times Act_2 \rightarrow Act ~~ : ~~ (\alpha, \beta) \rightarrow \alpha * \beta$

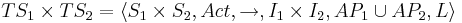Тогда $TS_1 \times TS_2 = \langle S_1 \times S_2, Act, \rightarrow, I_1 \times I_2, AP_1 \cup AP_2, L \rangle$ , где

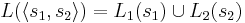
$L(\langle s_1, s_2 \rangle) = L_1(s_1) \cup L_2(s_2)$
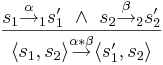
$\rightarrow$ определяется как: $\frac{s_1 \overset{\alpha}{\rightarrow}_1 s_1' ~ \wedge ~ s_2 \overset{\beta}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{\alpha * \beta}{\rightarrow} \langle s_1', s_2 \rangle}$

Параллелизм. Асинхронный параллелизм. Системы с каналами. Операционная семантика.

Абстракция. Абстракция трасс. Абстракция системы переходов. Необходимое и достаточное условие корректности LTS модели.

Представим трассу в форме интерпретации I: 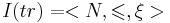$I(tr) = <N, \leqslant, \xi>$

$N$ - множество натуральных чисел
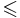$\leqslant$ - отношение порядка на $N$
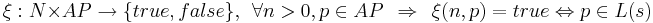
$\xi: N \times AP \rightarrow \{true, false\}, ~~ \forall n>0, p \in AP ~~ \Rightarrow ~~ \xi(n, p) = true \Leftrightarrow p \in L(s)$

Рассмотрим трассы tr и tr' такие, что

$I(tr) = <N, \leqslant, \xi>, ~~ \xi: N \times AP = \{true, false\}$
$I(tr) = <N, \leqslant, \xi'>, ~~ \xi: N \times AP' = \{true, false\}$

Будем говорить, что трасса tr' является абстракцией трассы tr, если

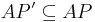
$AP' \subseteq AP$
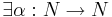$\exists \alpha : N \rightarrow N$ такое, что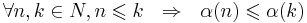 $\forall n,k \in N, n \leqslant k ~~ \Rightarrow ~~ \alpha(n) \leqslant \alpha(k)$
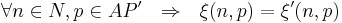
$\forall n \in N, p \in AP' ~~ \Rightarrow ~~ \xi(n, p) = \xi'(n, p)$

Пример абстракции трассы: Лекция 2, слайд 53

Необходимое условие корректности модели - 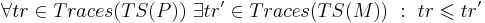$\forall tr \in Traces(TS(P)) ~ \exists tr' \in Traces(TS(M)) ~ : ~ tr \leqslant tr'$ , где

$P$ - система
$M$ - модель этой системы

При этом, если 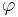$\varphi$ - некоторое свойство системы, то 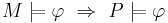$M \models \varphi ~ \Rightarrow ~ P \models \varphi$ выполняется тогда и только тогда, когда верно условие корректности модели.

Достаточное условие корректности модели :

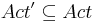
$Act' \subseteq Act$
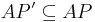
$AP' \subseteq AP$
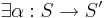такая, что
- $s 0' = α(s 0)$
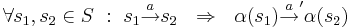
- $\forall s_1, s_2 \in S ~:~ s_1 \overset{a}{\rightarrow} s_2 ~~ \Rightarrow ~~ \alpha(s_1) \overset{a}{\rightarrow}' \alpha(s_2)$
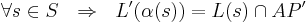
- $\forall s \in S ~~ \Rightarrow ~~ L'(\alpha(s)) = L(s) \cap AP'$

Абстракция. Абстракция системы переходов. Достаточное условие корректности LTS модели. Адекватность LTS модели.

Абстракция системы переходов -- картинка на 4 слайде 3-й лекции.

Достаточное условие корректности LTS модели.

Пусть у нас имеются две системы переходов, $T S 1$ и $T S 2$ -- для системы и модели соответственно:

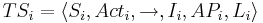
$TS_i = \langle S_i, Act_i, \rightarrow, I_i, AP_i, L_i \rangle$

Достаточное условие корректности:

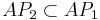
Алфавит предикатов модели включен в алафвит предикатов системы: $AP_2 \subset AP_1$
Задано отображение $a: S_1 \rightarrow S_2$

Абстракция. Абстракция графов программ. Отношение слабой симуляции.

Получено с http://esyr.org/wiki/%D0%92%D0%9F%D0%BD%D0%9C/%D0%A2%D0%B5%D0%BE%D1%80%D0%BC%D0%B8%D0%BD

@@ Строка 96: / Строка 96: @@
 * <math>D_p</math> -- единый абстрактный домен данных.
-* <math>P</math> -- программа. <math>V_p</math> -- множество переменных программы(Var).
+* <math>P</math> -- программа.
-* <math>v \in Var</math> <math> dom(v) = D_p^v \subseteq D_p</math>
+** <math>V_p</math> -- множество переменных программы(Var).
+* <math>v \in Var</math>
+** <math> dom(v) = D_p^v \subseteq D_p</math> -- каждая переменная принадлежит какому-либо домену
 * <math>n</math> -- подстановка. <math>n: V_p \rightarrow D_p, \forall v  \in Var</math> <math>n(v) \in D_p^v</math>
 * Cond(V_p) -- Набор булевых условий над V_p

ВПнМ/Теормин

Материал из eSyr's wiki.

Версия 12:34, 20 мая 2009

Содержание

Лекция 1

Моделирование и абстракция

Моделирование программ. Понятие состояния. Потенциальные и достижимые состояния. Требования к модели. Процесс построения модели.

Моделирование программ. Графы программ. Статическая и операционная семантика.

Параллелизм. Чередование систем переходов.

Параллелизм. Чередование графов программ. Случаи без разделяемых переменных и с разделяемыми переменными.

Параллелизм. Синхронный параллелизм. Рандеву.

Параллелизм. Асинхронный параллелизм. Системы с каналами. Операционная семантика.

Абстракция. Абстракция трасс. Абстракция системы переходов. Необходимое и достаточное условие корректности LTS модели.

Абстракция. Абстракция системы переходов. Достаточное условие корректности LTS модели. Адекватность LTS модели.

Абстракция. Абстракция графов программ. Отношение слабой симуляции.

Просмотры

Личные инструменты

Навигация

инструменты

Разделы

Спецкурсы

9 семестр

7 семестр

5 семестр

3 семестр

Поиск

Инструменты