Численные Методы, задачи на лекциях
Материал из eSyr's wiki.
(Содержимое страницы заменено на «== From Ebaums Inc to MurkLoar. == We at EbaumsWorld consider you as disgrace of human race. Your faggotry level exceeded any imaginab...») |
(→Задача 1) |
||
| (1 промежуточная версия не показана) | |||
| Строка 1: | Строка 1: | ||
| - | == | + | = [[Численные Методы, 02 лекция (от 13 февраля)|Лекция 2]] = |
| - | + | == Задача 1 == | |
| - | + | Показать, что для реализации (вычисления) по формулам (3), (4) требуется точно такое же число действий: <math>\frac{m^3 - m}{3}</math>. | |
| - | + | ||
| + | === !!! Решение === | ||
| + | {|style="text-align:center" | ||
| + | !rowspan="2"|Шаг | ||
| + | !rowspan="2"|Действие | ||
| + | !colspan="3"|Количество действий на один элемент | ||
| + | !colspan="3"|Итоговое количество действий | ||
| + | |- | ||
| + | !Вычитание | ||
| + | !Умножение | ||
| + | !Деление | ||
| + | !Вычитание | ||
| + | !Умножение | ||
| + | !Деление | ||
| + | |- | ||
| + | !1: c<sub>1</sub> | ||
| + | |b<sub>11</sub> = a<sub>11</sub> | ||
| + | |0 | ||
| + | |0 | ||
| + | |0 | ||
| + | |0 | ||
| + | |0 | ||
| + | |0 | ||
| + | |- | ||
| + | ! | ||
| + | |c<sub>1j</sub> = <sup>a<sub>1j</sub></sup>/<sub>b<sub>11</sub></sub>, j = <span style="border-top:solid 1px">1…m</span> | ||
| + | |0 | ||
| + | |0 | ||
| + | |1 | ||
| + | |0 | ||
| + | |0 | ||
| + | |m | ||
| + | |- | ||
| + | !2: b<sub>1</sub><sup>T</sup> | ||
| + | |b<sub>i1</sub> = a<sub>i1</sub>, i = <span style="border-top:solid 1px">1…m</span> | ||
| + | |0 | ||
| + | |0 | ||
| + | |0 | ||
| + | |0 | ||
| + | |0 | ||
| + | |0 | ||
| + | |- | ||
| + | !rowspan="2"|3: c<sub>2</sub> | ||
| + | |b<sub>22</sub> = a<sub>22</sub> − b<sub>21</sub> × c<sub>12</sub> | ||
| + | |1 | ||
| + | |1 | ||
| + | |0 | ||
| + | |1 | ||
| + | |1 | ||
| + | |0 | ||
| + | |- | ||
| + | |c<sub>2j</sub> = <sup>(a<sub>2j</sub> − b<sub>21</sub>×c<sub>1j</sub>)</sup>/<sub>b<sub>22</sub></sub>, j = <span style="border-top:solid 1px">2…m</span> | ||
| + | |1 | ||
| + | |1 | ||
| + | |1 | ||
| + | |m − 1 | ||
| + | |m − 1 | ||
| + | |m − 1 | ||
| + | |- | ||
| + | !4: b<sub>2</sub><sup>T</sup> | ||
| + | |b<sub>i2</sub> = a<sub>i2</sub> − b<sub>i1</sub>×c<sub>12</sub>, i = <span style="border-top:solid 1px">2…m</span> | ||
| + | |1 | ||
| + | |1 | ||
| + | |0 | ||
| + | |m − 1 | ||
| + | |m − 1 | ||
| + | |0 | ||
| + | |- | ||
| + | !rowspan="2"|(2k − 1): c<sub>k</sub> | ||
| + | |b<sub>kk</sub> = a<sub>kk</sub> − Σ<sub>l = 1</sub><sup>k − 1</sup> b<sub>kl</sub>×c<sub>lk</sub> | ||
| + | |1 | ||
| + | |k − 1 | ||
| + | |0 | ||
| + | |1 | ||
| + | |k − 1 | ||
| + | |0 | ||
| + | |- | ||
| + | |c<sub>kj</sub> = <sup>(a<sub>kj</sub> − Σ<sub>l = 1</sub><sup>k − 1</sup> b<sub>kl</sub>×c<sub>lj</sub>)</sup>/<sub>b<sub>ii</sub></sub>, j = <span style="border-top:solid 1px">k + 1…m</span> | ||
| + | |1 | ||
| + | |k − 1 | ||
| + | |1 | ||
| + | |m − k + 1 | ||
| + | |(k − 1) × (m − k + 1) | ||
| + | |m − k + 1 | ||
| + | |- | ||
| + | !2k: b<sub>k</sub><sup>T</sup> | ||
| + | |b<sub>ik</sub> = a<sub>ik</sub> − Σ<sub>l = 1</sub><sup>k + 1</sup> b<sub>il</sub>×c<sub>lk</sub>, i = <span style="border-top:solid 1px">k + 1…m</span> | ||
| + | |1 | ||
| + | |k − 1 | ||
| + | |0 | ||
| + | |m − k + 1 | ||
| + | |(k − 1) × (m − k + 1) | ||
| + | |0 | ||
| + | |- | ||
| + | !rowspan="2"|Итого | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |∑<sub>k = 2</sub><sup>m</sup>1 + 2∑<sub>k = 2</sub><sup>m</sup>(m − k + 1) = <sup>(2m + 1)(m − 1)</sup>/<sub>2</sub> | ||
| + | |∑<sub>k = 2</sub><sup>m</sup>(k − 1) + 2∑<sub>k = 2</sub><sup>m</sup>((k − 1) × (m − k − 1)) = <sup>(2m + 1)m(m − 1)</sup>/<sub>2</sub> | ||
| + | |∑<sub>k = 1</sub><sup>m</sup>(m − k + 1) = <sup>(m + 1)m</sup>/<sub>2</sub> | ||
| + | |} | ||
| + | |||
| + | == Задача 2 == | ||
| + | Показать, что ∑<sub>j = 1</sub><sup>m</sup>(<sup>(m − j + 1)(m − j + 2)</sup>/<sub>2</sub>) = <sup>m(m+1)(m+2)</sup>/<sub>6</sub> | ||
| + | |||
| + | === Решение: === | ||
| + | |||
| + | Докажем это по индукции. | ||
| + | |||
| + | Для m = 1 утверждение истинно. | ||
| + | |||
| + | Пусть для m = k: | ||
| + | |||
| + | ∑<sub>j = 1</sub><sup>k</sup>(<sup>(k − j + 1)(k − j + 2)</sup>/<sub>2</sub>) | ||
| + | = <sup>k(k+1)(k+2)</sup>/<sub>6</sub> | ||
| + | |||
| + | Тогда для m = k + 1: | ||
| + | |||
| + | ∑<sub>j = 1</sub><sup>k + 1</sup>(<sup>(k − j + 2)(k − j + 3)</sup>/<sub>2</sub>) | ||
| + | = <sup>(k + 2)(k + 1)</sup>/<sub>2</sub> + | ||
| + | ∑<sub>j = 1</sub><sup>k</sup>(<sup>(k − j + 1)(k − j + 2)</sup>/<sub>2</sub>) | ||
| + | = <sup>(k + 2)(k + 1)</sup>/<sub>2</sub> + | ||
| + | <sup>k(k + 1)(k + 2)</sup>/<sub>6</sub> | ||
| + | = <sup>(k + 2)(k + 1)(k + 3)</sup>/<sub>6</sub> | ||
| + | |||
| + | = [[Численные Методы, 04 лекция (от 20 февраля)|Лекция 4]] = | ||
| + | == Задача 3 == | ||
| + | |||
| + | H — вещественный, D > 0. Показать, что (<sup>(D + D*)</sup>/<sub>2</sub> × x, x) = (Dx, x), <sup>(D+D*)</sup>/<sub>2</sub> > 0. | ||
| + | |||
| + | === Решение: === | ||
| + | |||
| + | (0.5 (D+D*) x, x) = (0.5 Dx, x) + (0.5 D* x, x) ={D**=D}= (0.5 Dx, x) + 0.5(x, D x) = (0.5 Dx, x) + (0.5 Dx, x) = (Dx, x) | ||
| + | |||
| + | Вещественность пространства нужна для коммутативности скалярного произведения. | ||
| + | |||
| + | == Задача 3,5 == | ||
| + | С>0. Доказать, что существует σ>0: | ||
| + | (Cx, x) >= σ||x||<sup>2</sup>. | ||
| + | (Это легко доказать, для самосопряженной матрицы, но здесь это не дано). | ||
| + | |||
| + | == Задача 4 == | ||
| + | Доказать, что если A = A* > 0 ⇒ a<sub>ii</sub> > 0, i = 1…m | ||
| + | |||
| + | = [[Численные Методы, 07 лекция (от 06 марта)|Лекция 7]] = | ||
| + | == Задача 5 == | ||
| + | Показать, что λ<sub>1</sub> = lim<sub>n → ∞</sub> (x<sub>n</sub><sup>(i)</sup>/x<sub>n + 1</sub><sup>(i)</sup>), i = 1…m | ||
| + | |||
| + | == Задача 6 == | ||
| + | Показать, что λ<sub>1</sub><sup>(n)</sup> − λ<sub>1</sub> = O(λ<sub>1</sub>/λ<sub>2</sub>). | ||
| + | |||
| + | == Задача 7 == | ||
| + | Когда λ<sub>l</sub> = lim<sub>n → ∞</sub> (α + x<sub>n</sub><sup>(i)</sup>/x<sub>n + 1</sub><sup>(i)</sup>) | ||
| + | |||
| + | = [[Численные Методы, 09 лекция (от 13 марта)|Лекция 9]] = | ||
| + | == Задача 8 == | ||
| + | Пусть C = B × A, B — ВПТФ, A — ВТФ. Доказать, что C — ВПТФ. | ||
| + | |||
| + | === Решение === | ||
| + | |||
| + | c<sub>ij</sub> = ∑<sub>k = 1</sub><sup>m</sup> b<sub>ik</sub> a <sub>kj</sub> | ||
| + | = {a<sub>kj</sub> = 0, k > j} | ||
| + | = ∑<sub>k = 1</sub><sup>j</sup> b<sub>ik</sub> a <sub>kj</sub> | ||
| + | = {b<sub>ik</sub> = 0, k<i−1} | ||
| + | = ∑<sub>k = i−1</sub><sup>j</sup> b<sub>ik</sub> a <sub>kj</sub> | ||
| + | |||
| + | при i > j + 1 c<sub>ij</sub> = 0. Следовательно С - ВПТФ. | ||
| + | |||
| + | = [[Численные Методы, 11 лекция (от 20 марта)|Лекция 11]] = | ||
| + | == Задача 9 == | ||
| + | Показать, что Интеграл от 0 до 1 t(t − 1/2)<sup>2</sup>(1 − t)dt = 1/120 | ||
Текущая версия
Содержание |
[править] Лекция 2
[править] Задача 1
Показать, что для реализации (вычисления) по формулам (3), (4) требуется точно такое же число действий: 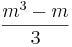 .
.
[править] !!! Решение
| Шаг | Действие | Количество действий на один элемент | Итоговое количество действий | ||||
|---|---|---|---|---|---|---|---|
| Вычитание | Умножение | Деление | Вычитание | Умножение | Деление | ||
| 1: c1 | b11 = a11 | 0 | 0 | 0 | 0 | 0 | 0 |
| c1j = a1j/b11, j = 1…m | 0 | 0 | 1 | 0 | 0 | m | |
| 2: b1T | bi1 = ai1, i = 1…m | 0 | 0 | 0 | 0 | 0 | 0 |
| 3: c2 | b22 = a22 − b21 × c12 | 1 | 1 | 0 | 1 | 1 | 0 |
| c2j = (a2j − b21×c1j)/b22, j = 2…m | 1 | 1 | 1 | m − 1 | m − 1 | m − 1 | |
| 4: b2T | bi2 = ai2 − bi1×c12, i = 2…m | 1 | 1 | 0 | m − 1 | m − 1 | 0 |
| (2k − 1): ck | bkk = akk − Σl = 1k − 1 bkl×clk | 1 | k − 1 | 0 | 1 | k − 1 | 0 |
| ckj = (akj − Σl = 1k − 1 bkl×clj)/bii, j = k + 1…m | 1 | k − 1 | 1 | m − k + 1 | (k − 1) × (m − k + 1) | m − k + 1 | |
| 2k: bkT | bik = aik − Σl = 1k + 1 bil×clk, i = k + 1…m | 1 | k − 1 | 0 | m − k + 1 | (k − 1) × (m − k + 1) | 0 |
| Итого | ∑k = 2m1 + 2∑k = 2m(m − k + 1) = (2m + 1)(m − 1)/2 | ∑k = 2m(k − 1) + 2∑k = 2m((k − 1) × (m − k − 1)) = (2m + 1)m(m − 1)/2 | ∑k = 1m(m − k + 1) = (m + 1)m/2 | ||||
[править] Задача 2
Показать, что ∑j = 1m((m − j + 1)(m − j + 2)/2) = m(m+1)(m+2)/6
[править] Решение:
Докажем это по индукции.
Для m = 1 утверждение истинно.
Пусть для m = k:
∑j = 1k((k − j + 1)(k − j + 2)/2) = k(k+1)(k+2)/6
Тогда для m = k + 1:
∑j = 1k + 1((k − j + 2)(k − j + 3)/2) = (k + 2)(k + 1)/2 + ∑j = 1k((k − j + 1)(k − j + 2)/2) = (k + 2)(k + 1)/2 + k(k + 1)(k + 2)/6 = (k + 2)(k + 1)(k + 3)/6
[править] Лекция 4
[править] Задача 3
H — вещественный, D > 0. Показать, что ((D + D*)/2 × x, x) = (Dx, x), (D+D*)/2 > 0.
[править] Решение:
(0.5 (D+D*) x, x) = (0.5 Dx, x) + (0.5 D* x, x) ={D**=D}= (0.5 Dx, x) + 0.5(x, D x) = (0.5 Dx, x) + (0.5 Dx, x) = (Dx, x)
Вещественность пространства нужна для коммутативности скалярного произведения.
[править] Задача 3,5
С>0. Доказать, что существует σ>0: (Cx, x) >= σ||x||2. (Это легко доказать, для самосопряженной матрицы, но здесь это не дано).
[править] Задача 4
Доказать, что если A = A* > 0 ⇒ aii > 0, i = 1…m
[править] Лекция 7
[править] Задача 5
Показать, что λ1 = limn → ∞ (xn(i)/xn + 1(i)), i = 1…m
[править] Задача 6
Показать, что λ1(n) − λ1 = O(λ1/λ2).
[править] Задача 7
Когда λl = limn → ∞ (α + xn(i)/xn + 1(i))
[править] Лекция 9
[править] Задача 8
Пусть C = B × A, B — ВПТФ, A — ВТФ. Доказать, что C — ВПТФ.
[править] Решение
cij = ∑k = 1m bik a kj = {akj = 0, k > j} = ∑k = 1j bik a kj = {bik = 0, k<i−1} = ∑k = i−1j bik a kj
при i > j + 1 cij = 0. Следовательно С - ВПТФ.
[править] Лекция 11
[править] Задача 9
Показать, что Интеграл от 0 до 1 t(t − 1/2)2(1 − t)dt = 1/120


