ВПнМ, примеры задач/Задача 1
Материал из eSyr's wiki.
(Различия между версиями)
ESyr01 (Обсуждение | вклад)
(Новая: == Задание == Будем считать состоянием модели значение счётчика команд (неявная переменная потока упра...)
К следующему изменению →
Версия 23:40, 24 апреля 2008
Содержание |
Задание
Будем считать состоянием модели значение счётчика команд (неявная переменная потока управления) и значения всех переменных заданной программы. Требуется:
- Оценить размер множества потенциальных состояний программы. Ответ обосновать. В обосновании описать множество потенциальных состояний.
- Оценить размер множества достижимых состояний программы. Ответ обосновать. В обосновании описать множество достижимых состояний.
- Построить LTS для значений параметра a = 1, b = 2, c =3. Описание LTS может быть как текстовым, так и графическим (например, выполненным при помощи средства GraphViz, http://www.graphviz.org).
Варианты
void
f (int a, int b, int c)
{
int x = 0, y = 0, z = 0;
x = 4;
y = 1;
z = a;
if (y > 6)
{
x = 2;
z = y + x;
if (z > c)
{
x = 10;
}
if (y > 6)
{
z = b;
}
else
{
x = 5;
}
y = 2;
y = 2;
}
y = 2;
}
Решение
Количество потенциальных состояний
void
f (int a, int b, int c)
{
0: int x = 0, y = 0, z = 0;
1: x = 4;
2: y = 1;
3: z = a;
4: if (y > 6)
{
5: x = 2;
6: z = y + x;
7: if (z > c)
{
8: x = 10;
}
9: if (y > 6)
{
10: z = b;
}
else
{
11: x = 5;
}
12: y = 2;
13: y = 2;
}
14: y = 2;
}
Количество потенциальных состояний (сумма состояний для каждого оператора, всего переменных 6 в каждой точке программы, для каждой 2^32 вариантов): 15 * 2^(32 * 6)
Количество достижимых состояний
a b c x y z
void
f (int a, int b, int c)
{
0: int x = 0, y = 0, z = 0; 2^32 2^32 2^32 1 1 1
1: x = 4; 2^32 2^32 2^32 1 1 1
2: y = 1; 2^32 2^32 2^32 1 1 1
3: z = a; 2^32 2^32 2^32 1 1 2^32
4: if (y > 6) 2^32 2^32 2^32 1 1 2^32
{
5: x = 2; 0 0 0 0 0 0
6: z = y + x; 0 0 0 0 0 0
7: if (z > c) 0 0 0 0 0 0
{
8: x = 10; 0 0 0 0 0 0
}
9: if (y > 6) 0 0 0 0 0 0
{
10: z = b; 0 0 0 0 0 0
}
else
{
11: x = 5; 0 0 0 0 0 0
}
12: y = 2; 0 0 0 0 0 0
13: y = 2; 0 0 0 0 0 0
}
14: y = 2; 2^32 2^32 2^32 1 1 2^32
}
Количество достижимых состояний для программы — сумма количества достижимых состояний для каждой точки программы, что, в свою очередь — произведение количество состояний переменных в данной точке. Итого: (2^96 + 2^128) * 3.
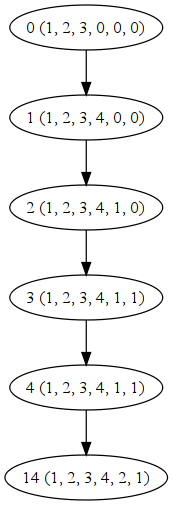
LTS
digraph LTS1 {
0 [label="0 (1, 2, 3, 0, 0, 0)"];
1 [label="1 (1, 2, 3, 4, 0, 0)"];
2 [label="2 (1, 2, 3, 4, 1, 0)"];
3 [label="3 (1, 2, 3, 4, 1, 1)"];
4 [label="4 (1, 2, 3, 4, 1, 1)"];
14 [label="14 (1, 2, 3, 4, 2, 1)"];
0 -> 1 -> 2 -> 3 -> 4 -> 14;
}